9. Impedenza e angolo di fase
Da non perdere…
Esplora impedenza, corrente e tensione in un circuito RLC nell’applet più avanti in questa pagina.
Impedenza
L’impedenza di un circuito è la resistenza effettiva totale al flusso di corrente da una combinazione degli elementi del circuito.
Simbolo: Z
Unità: `Ω ‘
La tensione totale su tutti i 3 elementi (resistori, condensatori e induttori) è scritta
VRLC
Per trovare questa tensione totale, non possiamo semplicemente aggiungere le tensioni VR, VL e VC.
Perché VL e VC sono considerati immaginario quantità, abbiamo:
Impedenza VRLC = IZ
`Z = R + j(X_L− X_C)`
Ora, la grandezza (size o valore assoluto) di Z è data da:
`|Z/=sqrt(R^2+(X_L-X_C)^2`
Angolo di fase
`tan\ theta=(X_L-X_C)/R`
Angolo θ rappresenta l’angolo di fase tra la corrente e la tensione.
Confronta questo con l’angolo di fase che abbiamo incontrato in precedenza nei grafici di y = a sin (bx + c).
Esempio 1
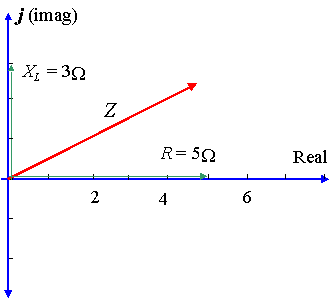
Un circuito ha una resistenza di `5\ Ω` in serie con una reattanza attraverso un induttore di `3\ Ω`. Rappresenta l’impedenza di un numero complesso, in forma polare.
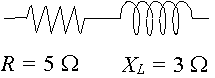
Risposta
In questo caso, `X_L= 3\ Ω` e `X_C= 0` cosi `X_L – X_C= 3\ Ω`.
Quindi in forma rettangolare, l’impedenza è scritta:
`Z = 5 + 3j\ Ω`
Usando la calcolatrice, la grandezza di Z è data da: `5.83`, e l’angolo `θ` (la differenza di fase) è dato da: `30.96^@`.
Quindi la tensione porta la corrente di `30.96^@’, come mostrato nel diagramma.
Presentando Z come un numero complesso (in forma polare), abbiamo:
`Z = 5.83 3 30.96^@\ Ω`.
Esempio 2(a)
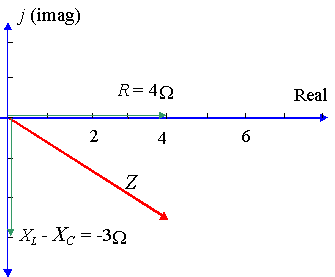
Un particolare circuito ca ha un resistore di `4\ Ω`, una reattanza su un induttore di `8\ Ω` e una reattanza su un condensatore di `11\ Ω`. Esprimere l’impedenza del circuito come un numero complesso in forma polare.
Risposta
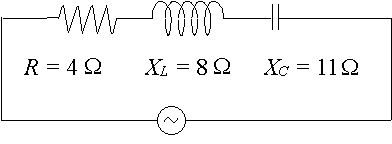
In questo caso, abbiamo: `X_L – X_C= 8 – 11 = -3\ Ω
`Z = 4 – 3j\ Ω` in forma rettangolare.
Ora per esprimerlo in forma polare:
Usando la calcolatrice, troviamo `r = 5` e ` θ = -36.87^@`.
So `Z = 5 ∠ -36.87^@\ Ω`
Grafico RLC interattivo
Di seguito è riportato un grafico interattivo con cui giocare (non è un’immagine statica). È possibile esplorare l’effetto di un resistore, condensatore e induttore sull’impedenza totale in un circuito CA.
Attività per questo interattivo
- In primo luogo, basta giocare con i cursori. Puoi:
Trascinare il cursore superiore a sinistra oa destra per variare l’impedenza dovuta al resistore, `R`,
Trascinare il cursore XL verso l’alto o verso il basso per variare l’impedenza dovuta all’induttore, `X_L`, e
Trascinare il cursore XC verso l’alto o verso il basso per variare l’impedenza dovuta al condensatore, `X_C`. - Osservare gli effetti di diverse impedenze sui valori di XL-XC e Z.
- Osservare gli effetti di diverse impedenze su θ, l’angolo che la linea rossa “risultato” fa con l’orizzontale (in radianti).
- Considera i grafici di tensione e corrente nell’interattivo. Osservare la quantità di ritardo o di piombo come si cambiano i cursori.
- Cosa hai imparato giocando con questo interattivo?