2.5: Legge di Darcy-Flusso in un mezzo poroso
La legge di Darcy è fondamentale per comprendere molti rami della geologia, in particolare idrogeologia. Prima di guardare la legge e cosa può dirci, diamo un’occhiata a come è stato sviluppato. La legge di Darcy prende il nome da Henry Darcy, un ingegnere francese del 19 ° secolo che sviluppò un sistema di tubi pressurizzati sotterranei per fornire acqua intorno alla città di Digione. Il sistema, che forniva anche acqua alle famose fontane di Digione, rivoluzionò i sistemi idrici e fognari della città. Il sistema non richiedeva pompe ed era azionato esclusivamente per gravità. Durante il processo di sviluppo del nuovo sistema, Darcy ha condotto una serie di esperimenti in cui ha cercato di spostare l’acqua utilizzando esclusivamente la gravità.
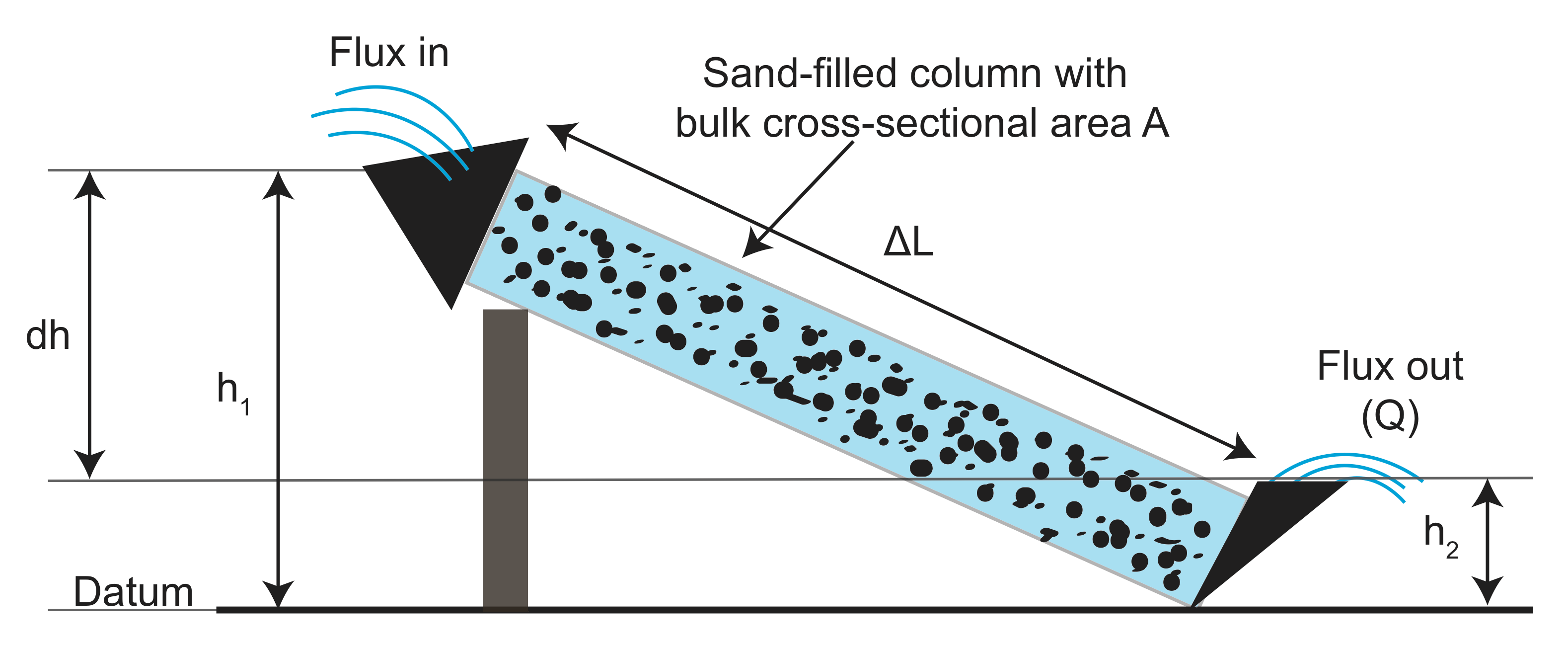
gli esperimenti, i dati raccolti sulla lunghezza del canale (\(L\)), l’area della sezione trasversale del canale artificiale (\(A\)), la differenza di altezza (\(h_1 – h_2\)), e il flusso di acqua in uscita \(Q\) con e senza granulare (filtro) materiale nel canale. Ha quindi tracciato la misura del flusso normalizzata dall’area rispetto al rapporto tra la differenza di altezza e la lunghezza del canale (\( \frac{h_1 – h_2}{l}\)). Quello che ha scoperto è che esiste una relazione lineare e la pendenza dipende dal materiale granulare che ha usato nel canale:
\
che può essere riscritto come derivato,
\
dove \(K\) è la conduttività idraulica e \(\frac{dh}{dx}\) è il gradiente idraulico. \(Q\), il tasso di scarico totale, ha unità di \ (\frac {m^3} {s}\), il volume di acqua per volta. Il segno negativo è dovuto al fatto che il fluido scorre verso il basso (negativo) il gradiente idraulico da valori più alti a valori più bassi.
La conduttività idraulica è un parametro fisico che spiega quanto facilmente il fluido può muoversi attraverso lo spazio dei pori per il materiale. Negli esperimenti originali di Darcy, ha usato sabbie con diverse granulometrie, tuttavia, la conduttività idraulica può essere determinata anche per le rocce solide, poiché la maggior parte delle rocce ha uno spazio dei pori.
Seguendo gli esperimenti originali di Darcy, sono stati fatti ulteriori lavori per comprendere le proprietà fisiche del fluido e della roccia che determinano l’effettiva conduttività idraulica. Da questi esperimenti si è constatato che,
\
dove \(k\) è la permeabilità intrinseca dei mezzi porosi (solido), \(\eta\) è la viscosità dinamica del fluido, e \(\gamma = \rho g\) è il peso specifico del fluido, che dipende dalla densità del fluido, \(\rho\) e la gravità, \(g\).
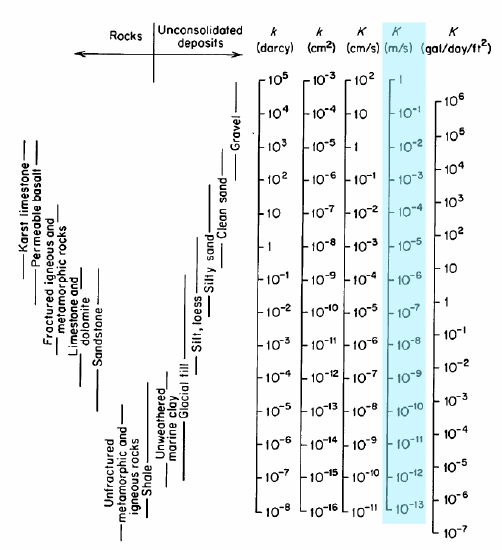
La colonna evidenziata nella figura è K, la conduttività idraulica in \(\frac{m}{s}\); queste sono le unità che useremo. La conduttività idraulica è talvolta riportata anche in termini di permeabilità intrinseca, \ (k\), con unità di darcys o cm2. L’intera gamma di valori per la conduttività idraulica è 1-10-13 \(\frac{m} {s}\). Esperimenti come quelli di Darcy sono usati per misurare K in materiali reali.
Il tasso di scarico di \(Q\) è un volume di flusso (\(m^3/s\)), ma di solito pensiamo che il flusso del fluido in termini di velocità o la velocità. Scarica domande possono essere riorganizzate dividendo per l’area per definire il Darcy di Flusso
\ \]
in termini di permeabilità intrinseca e gradiente di pressione,
\
dove \(\eta\) è la viscosità del fluido (vedi sotto per la derivazione dell’equazione di secondo).
È importante notare che il flusso di Darcy non è uguale alla velocità del fluido, anche se è in unità di velocità. La velocità del fluido si trova attraverso la velocità lineare media (\(v_a\)), che è media della velocità di tutti i possibili percorsi del fluido attraverso il mezzo poroso: ma trovare questo valore non rientra nell’ambito di questa classe. Invece, noteremo che la velocità del fluido è
\
dove \(\varphi\) è la porosità e v è la velocità del fluido. La porosità, \ (\varphi\) è calcolata come rapporto tra il volume dello spazio vuoto e il volume totale di un materiale \(\varphi= \ frac{V_ {void}} {V_{tot}}\), ed è solitamente espressa come frazione tra 0 e 1 o come percentuale. Si noti che se \ (\varphi \ leq\) 1 allora la velocità del fluido è maggiore del flusso darcy.
Un altro termine che si pone quando si parla di flusso attraverso rocce e materiali non consolidati è la permeabilità. Mentre la porosità è la frazione effettiva di pori (vuoti) nella roccia, questi vuoti possono avere forme diverse e connettività diversa, che influenza la facilità con cui un fluido può muoversi attraverso lo spazio dei pori. La permeabilità è una misura della facilità con cui liquidi e gas possono passare attraverso una roccia. Più il materiale è consolidato, minore è la sua permeabilità. Quindi i materiali “sciolti” come la ghiaia hanno un’alta permeabilità. Alcune rocce possono anche avere permeabilità anisotropica, il che significa che i fluidi possono fluire facilmente in una direzione, ma non in un’altra. Un esempio di roccia con permeabilità anisotropica è uno scisto. I fluidi possono muoversi facilmente all’interno di uno strato dello scisto, ma non possono muoversi attraverso gli strati.
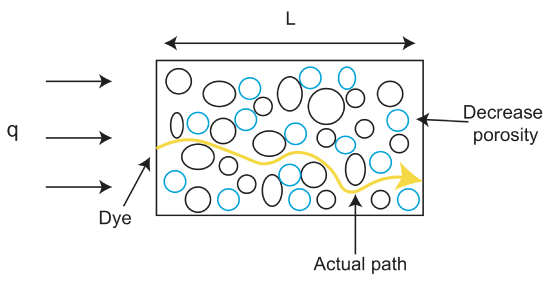
Velocità del fluido
Facciamo un esempio di base.
Ci viene dato che \(q=2\frac{m}{min}\) e \(\varphi\) è 25% e vogliono trovare la velocità del fluido.
Prima convertiamo 25% a 0.25.
Quindi, \(v= \ frac{2}{0.25} \ frac {m} {min}\)
e
\(v=8 \frac{m}{min}\) è la velocità del fluido.
Testa idraulica
Tornando agli esperimenti di Darcy, qual è il processo fisico che sta effettivamente guidando il flusso di fluido attraverso il canale?
Il termine \(\frac{dh}{dx} \) è indicato come la testa idraulica, che è la pressione del liquido dovuta al peso di un fluido rispetto a una posizione di riferimento: un gradiente di pressione. Tuttavia, \(\frac {dh} {dx}\) non ha unità di pressione per unità di lunghezza, quindi perché è chiamata testa idraulica?
Consideriamo quale sia la pressione nel canale negli esperimenti di Darcy. Per fare gli esperimenti, Darcy aveva un serbatoio d’acqua all’estremità superiore del canale che forniva un livello costante di acqua nella parte superiore del canale, equivalente all’altezza del canale, \(h_1\). Allo stesso modo, c’era un serbatoio sul fondo con un livello costante di acqua equivalente a \(h_2\). Pertanto la pressione del fluido in ciascuno dei serbatoi dovuta al peso dell’acqua è data da \(P = \rho g h\). Il gradiente di pressione tra la parte superiore e la parte inferiore del pennacchio è quindi
\
o
\
Sostituendo nell’Darcy Legge,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
Richiamare, dall’alto che la conducibilità idraulica può essere scritto in termini di permeabilità intrinseca come \(K = k\frac{\gamma}{\eta}\), che è equivalente a \(k\frac{\rho g}{\eta} \) o riorganizzazione, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Pertanto, si può sostituire a dare due espressioni equivalenti per Darcy Legge, con uno in termini di gradiente in altezza,
\
e il secondo in termini di gradiente di pressione,
\
Quindi, \(\frac{dh}{dx}\) è chiamato l’idraulico di testa perché l’origine fisica del termine Legge di Darcy è il gradiente di pressione nel fluido, che spinge il flusso.
Acqua che esce da una falda acquifera
Facciamo ora un esempio calcolando la velocità del fluido dell’acqua che entra in una falda acquifera. Nello schizzo sotto l’altezza della falda acquifera segue la topografia sulla collina adiacente alla valle con il torrente. L’acqua scorre dall’alta pressione (altezza della testa) verso valle e lascia la falda acquifera al torrente. Possiamo usare la Legge di Darcy per stimare il tasso di flusso dell’acqua dalla falda acquifera.
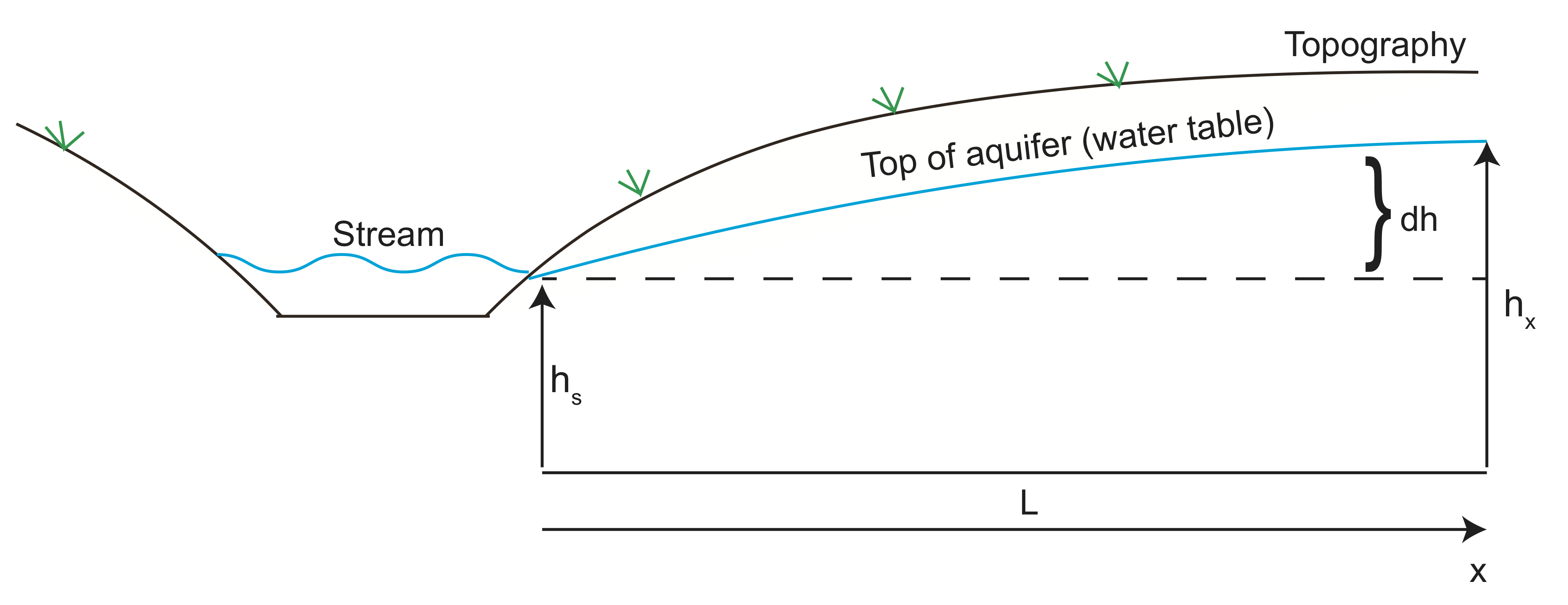
Utilizzando l’imaging geofisico, l’altezza della falda acquifera si trova a 10 m (\(dh\)) sopra l’altezza del flusso a circa 100 metri (\(L\)) di distanza. Supponiamo che la conduttività idraulica sia \( K=10^{-6}\) m / s e la porosità sia \(\varphi=30\)%.
Il darcy di flusso è
\
\
\
La velocità del fluido è
\
\
\
\

Flusso laminare contro flusso turbolento
Una delle ipotesi implicite nella legge di Darcy è che il flusso sia laminare. Il flusso laminare è caratterizzato come costituito da strati sottili o lamine di fluido che si muovono parallele l’una all’altra. Al contrario, il flusso turbolento è caratterizzato da vortici, vortici e vortici, in cui gli strati adiacenti di fluido divergono e prendono diversi percorsi a valle.
Un modo per quantificare se un fluido è laminare o turbolento è calcolando il numero di Reynold per il flusso, definito come
\
Il numero di Reynold si trova considerando i due termini nel bilancio della quantità di moto per il flusso. Il primo termine è la forza inerziale per unità di volume, che guida il flusso, \(\rho u \ frac {du} {dx}\). Il secondo termine è la forza viscosa per unità di volume, che resiste al flusso, \(\eta \ frac{d ^ 2u} {dx^2}\). Questi due termini devono essere bilanciati, quindi possiamo impostarli uguali,
\
Successivamente, riscriviamo i termini, in modo semplificato per catturare solo le dimensioni rilevanti delle variabili. Per fare, passiamo attraverso quella che viene chiamata analisi dimensionale, in cui sostituiamo ogni variabile, con un valore di riferimento, volte una forma non dimensionale della variabile.
Ad esempio per il termine \(x\) viene riscritto come solo \(L x’\), dove \(L\) è la lunghezza di riferimento (la profondità del fluido) e \(x’\) è la distanza non dimensionale. Allo stesso modo, lasciamo \(u = u_o u’\). Sostituendo questi nell’equazione, si ottiene
\
poi si uniscono i valori costanti davanti
\
si noti che la combinazione delle variabili di fronte si trova il numero di Reynold
\
in cui le variabili sono \(u_o\) velocità di flusso, L di liquido di profondità, e le variabili di cui abbiamo già visto in precedenza, \(\rho\) densità del fluido, e \(\eta\) viscosità del fluido. Passando attraverso questa analisi, troviamo che qualsiasi flusso caratterizzato dall’equilibrio di questi due termini può essere confrontato semplicemente conoscendo il valore del numero di Reynolds. Ad esempio, se un flusso ha una viscosità che è 10 volte la viscosità in un altro flusso, i due flussi si comportano lo stesso è la densità (o velocità o lunghezza) è anche aumentato di un fattore 10 per il caso maggiore viscosità; cioè, il numero di Reynolds per i due flussi è lo stesso.
Per avere un flusso Darcy, il numero di Reynold deve essere inferiore a circa 1-10 (laminare). Per \(Re > 1-10 \) il flusso non è strettamente laminare, ma non è ancora turbolento (non lineare, non laminare). Per avere un flusso turbolento, il numero di Reynold deve essere maggiore di circa 2000.
Comprendendo che le costanti nel numeratore e nel denominatore influenzano le caratteristiche del flusso in modo opposto, aiuta anche a pensare a come si comporteranno diversi fluidi in condizioni esterne simili. Ad esempio, un fluido più denso che ha anche una velocità veloce avrà un Re più alto e esibirà un comportamento turbolento. Al contrario, un fluido come il ghiaccio che ha un’alta viscosità e si muove molto lentamente avrà un basso Re e probabilmente avrà un flusso laminare. L’elevata viscosità del ghiaccio agisce per stabilizzare il flusso. Come altro esempio, si consideri che due fluidi potrebbero entrambi muoversi alla stessa velocità comportarsi in modo diverso se gli altri valori nel numero di Reynold \(\frac {\rho L} {\mu}\) sono diversi. Pertanto, il tipo di flusso dipende non solo dalla velocità del flusso, ma dalla combinazione di variabili nel numero di Reynold.
Applicazione del flusso di Darcy
La legge di Darcy è l’equazione principale che governa il flusso nelle falde acquifere e nei pozzi. Senza di essa, non saremmo in grado di perforare pozzi o capire il movimento dell’acqua nelle falde acquifere, specialmente nella Central valley della California, dove entrambe queste idee sono cruciali sia per la produttività agricola che per la subsidenza delle acque sotterranee.
