az átlag regressziója gyakori statisztikai jelenség, amely félrevezethet minket, amikor megfigyeljük a világot. Ha megtanuljuk felismerni az átlag regresszióját, az segíthet elkerülni az adatok félreértelmezését és a nem létező minták látását.

***

fontos, hogy minimalizáljuk a rossz ítélet eseteit, és az érvelésünk gyenge pontjait kezeljük. A regresszió megismerése segíthet nekünk.

Daniel Kahneman Nobel-díjas pszichológus könyvet írt olyan torzításokról, amelyek elhomályosítják az érvelésünket és torzítják a valóságérzékelésünket. Kiderült, hogy van egy sor logikai hiba, amit elkövetünk, mert az intuíciónk és az agyunk nem foglalkozik jól az egyszerű statisztikákkal. Az egyik hiba, amelyet a gyors és lassú gondolkodásban vizsgál, a hírhedt regresszió az átlag felé.

az átlaghoz való regresszió fogalmát először Sir Francis Galton dolgozta ki. A szabály az, hogy minden olyan komplex jelenséggel rendelkező sorozatban, amely sok változótól függ, ahol esély van, a szélsőséges eredményeket általában mérsékeltebbek követik.

A bölcsesség keresésében Peter Bevelin John példáját kínálja, aki elégedetlen volt az új alkalmazottak teljesítményével, ezért egy készségfejlesztő programba helyezte őket, ahol megmérte az alkalmazottak készségeit:

pontszámaik most magasabbak, mint az első teszten. John következtetése: “a készségfejlesztő program a készség javulását okozta.”Ez nem feltétlenül igaz. Magasabb pontszámuk az átlaghoz való regresszió eredménye lehet. Mivel ezeket az egyéneket úgy mérték, hogy a készségskála alacsony végén vannak, javulást mutattak volna, még akkor is, ha nem vették volna el a készségfejlesztő programot. A korábbi teljesítményüknek számos oka lehet-stressz, fáradtság, betegség, figyelemelterelés stb. Az igazi képességük talán nem változott.

teljesítményünk mindig az átlagos valódi teljesítmény körül változik. Az extrém teljesítmény legközelebb kevésbé szélsőséges. Miért? A mérések tesztelése soha nem lehet pontos. Minden mérés egy valós és egy véletlenszerű hibarészből áll. Ha a mérések szélsőségesek, akkor valószínűleg részben véletlen okozza őket. Az esély valószínűleg kevésbé járul hozzá a teljesítmény második méréséhez.

Ha valami egyik módjáról a másikra váltunk, pusztán azért, mert sikertelenek vagyunk, akkor nagyon valószínű, hogy legközelebb jobban cselekszünk, még akkor is, ha valami új módja egyenlő vagy rosszabb.

Ez az egyik oka annak, hogy veszélyes kis mintaméretekből extrapolálni, mivel az adatok esetleg nem reprezentálják az eloszlást. Ezért is állítja James March, hogy minél tovább marad valaki a munkahelyén, “annál kisebb a valószínű különbség a megfigyelt teljesítmény és a tényleges képesség között.”Bármi megtörténhet rövid távon, különösen minden erőfeszítést, amely magában foglalja a kombináció a készség és a szerencse. (A készség és a szerencse aránya az átlaghoz viszonyított regressziót is befolyásolja.)

regresszió az átlaghoz

az átlaghoz való regresszió hatásai gyakran megfigyelhetők a sportban, ahol a hatás sok indokolatlan spekulációt okoz.

a gondolkodás gyors és lassú, Kahneman emlékeztet néz férfi síugrás, fegyelem, ahol a végeredmény kombinációja két különálló ugrások. Az átlag regressziójának tudatában Kahneman megdöbbent, hogy meghallotta a kommentátor előrejelzéseit a második ugrásról. Azt írja:

Norvégia Volt egy nagy első ugrás; ő lesz feszült, abban a reményben, hogy megvédje a vezetést, és valószínűleg nem rosszabb” vagy “Svédország volt egy rossz első ugrás, és most már tudja, hogy nincs mit veszíteni, és nyugodt lesz, ami segít neki jobban csinálni.

Kahneman rámutat arra, hogy a kommentátor észrevette az átlag regresszióját, és előállt egy olyan történettel, amelyre nem volt ok-okozati bizonyíték (lásd: narratív tévedés). Ez nem azt jelenti, hogy a története nem lehet igaz. Talán, ha minden ugrás előtt megmérjük a pulzusszámot, azt látjuk, hogy nyugodtabbak, ha az első ugrás rossz volt. Azonban nem ez a lényeg. A lényeg az, hogy az átlag regressziója akkor történik, amikor a szerencse szerepet játszik, mint az első ugrás eredményében.

a sportból származó lecke minden olyan tevékenységre vonatkozik, ahol a véletlen szerepet játszik. Gyakran magyarázatokat csatolunk egy adott folyamatra gyakorolt hatásunkról annak előrehaladásához vagy hiányához.

a valóságban a teljesítmény tudománya összetett, helyzetfüggő, és gyakran sok, amit úgy gondoljuk, hogy a mi irányításunkban van, valóban véletlenszerű.

síugrások esetén az erős szél a jumperrel szemben a legjobb sportolóhoz vezet, aki közepes eredményeket mutat. Hasonlóképpen, az erős szél és a síviszonyok mellett egy középszerű jumper vezethet jelentős, de egy ideiglenes bump az ő eredménye. Ezek a hatások azonban megszűnnek, amint a feltételek megváltoznak, és az eredmények visszatérnek a normális szintre.

ez komoly hatással lehet a coachingra és a teljesítménykövetésre. A regresszió szabályai azt sugallják, hogy a teljesítmény vagy a bérbeadás értékelésekor a nyilvántartásokra kell támaszkodnunk, mint az adott helyzetek eredményei. Ellenkező esetben hajlamosak vagyunk csalódni.

amikor Kahneman előadást tartott az Izraeli légierőnek a hatékony képzés pszichológiájáról, az egyik tiszt megosztotta tapasztalatait, hogy a dicséret kiterjesztése alárendeltjeire rosszabb teljesítményhez vezetett, míg a szidás a későbbi erőfeszítések javulásához vezetett. Ennek következtében nagylelkűvé vált a negatív visszajelzésekkel, és meglehetősen óvatos lett, hogy túl sok dicséretet adjon.

Kahneman azonnal észrevette, hogy a munkahelyi átlag regressziója. Ő illusztrálta a tévhit egy egyszerű gyakorlat érdemes kipróbálni magát. Rajzolt egy kört egy táblára, majd megkérte a tiszteket egyenként, hogy dobjanak egy darab krétát a kör közepére, hátukkal a táblára nézve. Ezt követően megismételte a kísérletet, és az első és a második tárgyaláson rögzítette az egyes tisztek teljesítményét.

természetesen azok, akik hihetetlenül jól teljesítettek az első próbálkozásnál, rosszabbul jártak a második próbálkozásukon, és fordítva. A tévedés azonnal világossá vált: a teljesítményváltozás természetesen történik. Ez ismét nem azt jelenti, hogy a visszajelzés egyáltalán nem számít – talán igen, de a tisztnek nem volt bizonyítéka annak megállapításához.

A tökéletlen korreláció és esély

Ezen a ponton, akkor lehet, hogy vajon miért a regresszió az átlag történik, és hogyan tudjuk, hogy tisztában vagyunk vele, amikor ez bekövetkezik.

ahhoz, hogy megértsük az átlag regresszióját, először meg kell értenünk a korrelációt.

A -1 és 1 között változó két intézkedés közötti korrelációs együttható az általuk megosztott tényezők relatív súlyának mérése. Például két olyan jelenségnek, amelyekben kevés tényező van, például a palackozott víz fogyasztása az öngyilkossági arányhoz képest, közel 0-os korrelációs együtthatóval kell rendelkeznie. Vagyis, ha a világ minden országát megvizsgálnánk, és egy adott év öngyilkossági arányát terveznénk a palackozott víz egy főre jutó fogyasztásával szemben, a cselekmény egyáltalán nem mutatna mintát.

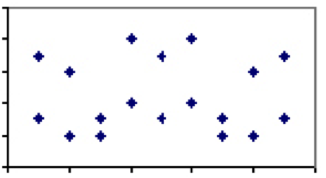
éppen ellenkezőleg, vannak olyan intézkedések, amelyek kizárólag ugyanazon tényezőtől függenek. Jó példa erre a hőmérséklet. Az egyetlen tényező, amely meghatározza a hőmérsékletet – a molekulák sebességét -, minden skálán oszlik meg, így minden Celsius-fok pontosan egy megfelelő értékkel rendelkezik Fahrenheitben. Ezért a Celsius-fok és a Fahrenheit hőmérsékletének korrelációs együtthatója 1, A telek pedig egyenes vonal lesz.

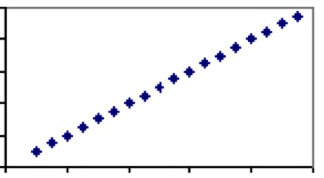
kevés olyan jelenség van az emberi tudományokban, amelyek korrelációs együtthatója 1. Van azonban bőven, ahol az összefüggés gyenge vagy mérsékelt, és van némi magyarázó erő a két jelenség között. Tekintsük a magasság és a súly közötti összefüggést, ami valahol 0 és 1 között lesz. Míg gyakorlatilag minden három éves lesz könnyebb és rövidebb, mint minden felnőtt ember, nem minden felnőtt férfi vagy hároméves azonos magasságú súlya azonos.

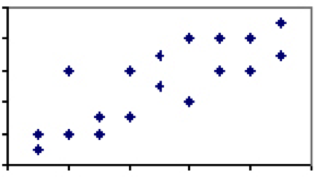
Ez a variáció és a megfelelő alacsonyabb fokú korreláció azt jelenti, hogy míg a magasság általában jó előrejelző, egyértelműen vannak más tényezők, mint a magasság a játékban. Ha két intézkedés korrelációja kevesebb, mint tökéletes, figyelnünk kell a regresszió hatására az átlagra.

Kahneman egy általános szabályt figyelt meg: ha a két pontszám közötti korreláció tökéletlen, akkor az átlag regressziója lesz.

ez eleinte zavarónak és nem túl intuitívnak tűnhet, de az átlaghoz való regresszió mértéke közvetlenül kapcsolódik a változók korrelációjának mértékéhez. Ez a hatás egy egyszerű példával illusztrálható.

tegyük fel, hogy egy partin vagy, és kérdezd meg, miért van az, hogy a rendkívül intelligens nők hajlamosak feleségül venni olyan férfiakat, akik kevésbé intelligensek, mint ők. A legtöbb ember, még azok is, az egyes képzési statisztika, gyorsan ugorj be a különféle ok-okozati magyarázatok kezdve elkerülése a verseny, hogy a félelem, a magány, hogy ezek a nők arcát. Az ilyen viták témája valószínűleg nagy vitát vált ki.

most mi van, ha megkérdezzük, hogy miért nem tökéletes a házastársak intelligencia pontszáma közötti korreláció? Ez a kérdés aligha olyan érdekes, és kevés a találgatás – mindannyian tudjuk, hogy ez igaz. A paradoxon abban rejlik,hogy a két kérdés algebrai szempontból egyenértékű. Kahneman elmagyarázza:

Ha a házastársak intelligenciája közötti korreláció kevesebb, mint tökéletes (és ha a férfiak és a nők átlagosan nem különböznek az intelligenciában), akkor matematikai elkerülhetetlen, hogy a rendkívül intelligens nők olyan férjekkel házasodjanak össze, akik átlagosan kevésbé intelligensek, mint ők (és természetesen fordítva). Az átlag megfigyelt regressziója nem lehet érdekesebb vagy megmagyarázhatóbb, mint a tökéletlen korreláció.

feltételezve, hogy a korreláció hiányos, annak esélye, hogy két partner a felső 1% – ot képviseli bármely jellemző szempontjából, sokkal kisebb, mint az egyik partner, amely a felső 1% – ot, a másik pedig az alsó 99% – ot képviseli.

az ok, hatás és kezelés

különösen óvatosnak kell lennünk az átlagos jelenség regressziójával, amikor két tényező közötti ok-okozati összefüggést próbálunk megállapítani. Amikor a korreláció tökéletlen, a legjobb mindig úgy tűnik, hogy rosszabb lesz, a legrosszabb pedig úgy tűnik, hogy idővel jobb lesz, függetlenül a további kezeléstől. Ez olyasmi, amit az általános média, sőt néha a képzett tudósok sem ismernek fel.

Tekintsük a Kahneman példáját:

az energiaitalokkal kezelt depressziós gyermekek jelentősen javulnak egy három hónapos időszak alatt. Ezt az újságcímet készítettem, de az a tény, hogy igaz: ha egy ideig depressziós gyermekek egy csoportját egy energiaitallal kezelte, akkor klinikailag jelentős javulást mutatna. Az is előfordul, hogy a depressziós gyermekek, akik egy kis időt töltenek a fejükön, vagy naponta húsz percig ölelnek egy macskát, szintén javulást mutatnak.

amikor ilyen címsorokon találkozik, nagyon csábító arra a következtetésre jutni, hogy az energiaitalok, a fejen állva vagy a macskák átölelve, mind tökéletesen életképes gyógymódok a depresszió számára. Ezek az esetek azonban ismét megtestesítik az átlag regresszióját:

a depressziós gyermekek szélsőséges csoport, depressziósabbak, mint a legtöbb más gyermek—és a szélsőséges csoportok idővel visszaállnak az átlaghoz. A depresszió pontszámai közötti korreláció az egymást követő tesztelési alkalmakkor kevesebb, mint tökéletes, tehát az átlag regressziója lesz: a depressziós gyermekek idővel valamivel jobbak lesznek, még akkor is, ha nem ölelnek meg macskákat, és nem isznak Red Bullt.

gyakran tévesen tulajdonítunk egy adott politikát vagy kezelést a hatás okaként, amikor a szélsőséges csoportok változása egyébként is megtörtént volna. Ez alapvető problémát jelent: honnan tudjuk, hogy a hatások valósak-e vagy egyszerűen a változékonyság miatt?

szerencsére van egy módja annak, hogy állapítsa meg a valódi javulás és regresszió az átlag. Ez az úgynevezett kontrollcsoport bevezetése, amely várhatóan csak a regresszióval javul. A kutatás célja annak meghatározása, hogy a kezelt csoport jobban javul-e, mint a regresszió.

a valós életben olyan helyzetekben, ahol bizonyos egyének vagy csapatok teljesítménye az egyetlen igazi referenciaérték, ahol a múltbeli teljesítmény és egyetlen kontrollcsoport sem vezethető be, a regresszió hatása nehéz lehet, ha nem lehetetlen szétválasztani. Összehasonlíthatjuk az iparági átlaggal, a kohorsz csoport társaival vagy a fejlődés történelmi arányaival, de ezek egyike sem tökéletes intézkedés.

***

szerencsére az átlagos jelenség regressziójának tudatosítása már nagyszerű első lépés a szerencse és a teljesítmény megértésének óvatosabb megközelítése felé.

ha van valami, amit meg kell tanulni a regressziótól az átlagig, akkor a pályarekordok fontossága, nem pedig az egyszeri sikertörténetekre támaszkodva. Remélem, hogy a következő alkalommal, amikor találkoznak egy extrém minőségű részben szabályozza véletlenül észre fogod venni, hogy a hatások valószínűleg visszafejlődnek az idő múlásával, majd állítsa be a várakozásokat ennek megfelelően.

mit kell olvasni következő

• frissítse a gondolkodás 113 mentális modellek magyarázható.
• olvassa el a második szintű gondolkodást, így elkerülheti a negatív következményeket.