a következő hallgatói kutatási jelentés készült Kardos Judit professzor matek 255 osztályára, amelyet a New Jersey-i Főiskolán tartottak. Ez egy 3-hitel bevezető tanfolyam volt a matematika történetében. Ezt a jelentést a végső fokozat 30% – ára számolták. Ez egy példa a fajta történelmi kutatás diákok tehetünk a másodlagos források.

Leonard Euler megoldása a Königsberg-híd problémájára

Königsberg

történetünk a 18. században kezdődik, a poroszországi Königsbergben, a Pregel-folyó partján. 1254-ben a teutonikus lovagok megalapították Königsberg városát Ottoker cseh király vezetésével, miután második keresztes hadjáratot indítottak a poroszok ellen. A középkorban Königsberg nagyon fontos várossá és kereskedelmi központtá vált, stratégiai elhelyezkedésével a folyón. A tizennyolcadik századi műalkotások Königsberget virágzó városként mutatják be, ahol a hajók flottái töltik meg a Pregelt, kereskedelmük kényelmes életmódot kínál mind a helyi kereskedők, mind családjaik számára. Az egészséges gazdaság lehetővé tette a város lakói számára, hogy hét hidat építsenek a folyón, amelyek többsége Kneiphof szigetéhez kapcsolódik; helyük a mellékelt képen látható .

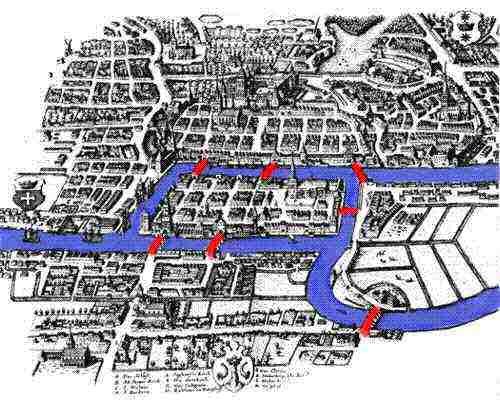
ahogy a folyó Kneiphof körül folyt, szó szerint pub udvarot jelent, és egy másik sziget, a várost négy különálló régióra osztotta. A hét hidat Kovács hídnak, összekötő hídnak, Zöld hídnak, kereskedői hídnak, Fahídnak, magas hídnak és Mézhídnak hívták. Lore szerint Königsberg polgárai vasárnap délutánokat töltöttek gyönyörű városuk körül. Séta közben a város lakói úgy döntöttek, hogy maguk számára létrehoznak egy játékot, céljuk az, hogy kidolgozzák azt a módot, amellyel sétálhatnak a városban, csak egyszer lépve át a hét hidat. Annak ellenére, hogy Königsberg egyik polgára sem tudott olyan útvonalat találni, amely lehetővé tenné számukra, hogy csak egyszer lépjenek át az egyes hidakon, még mindig nem tudták bizonyítani, hogy lehetetlen. Szerencséjükre Königsberg nem volt túl messze Szentpétervártól, a híres matematikus Leonard Euler otthonától.

Euler and The Bridge Problem

miért foglalkozna Euler egy olyan problémával, amely nem kapcsolódik a matematika területéhez? Miért töltene egy ilyen nagy matematikus sok időt egy olyan triviális problémával, mint a Königsberg híd problémája? Euler nyilvánvalóan elfoglalt ember volt, élete során több mint 500 könyvet és újságot tett közzé. Csak 1775-ben hetente átlagosan egy matematikai dolgozatot írt, és élete során a matematika mellett számos témában írt, többek között mechanikában, optikában, csillagászatban, navigációban és hidrodinamikában. Nem meglepő, hogy Euler úgy érezte, hogy ez a probléma triviális, egy 1736-os levélben Carl Leonhard Gottlieb Ehlernek, Danzig polgármesterének, aki a probléma megoldását kérte tőle:

. . . Így látod, nemes Uram, hogy ez a fajta megoldás viseli kevés kapcsolata a matematika, de nem értem, miért vársz egy matematikus előállítani, sokkal inkább, mint bárki más, a megoldás alapja, oka egyedül, a felfedezés nem függ semmilyen matematikai elv. Emiatt, nem tudom, miért még kérdéseket, amelyek viselik olyan kevés kapcsolat a matematika megoldani gyorsabban matematikusok, mint mások.

annak ellenére, hogy Euler triviálisnak találta a problémát, még mindig érdekelte. Egy ugyanebben az évben Giovanni Marinoni olasz matematikusnak és mérnöknek írt levélben Euler azt mondta:

Ez a kérdés annyira banális, de számomra figyelemre méltónak tűnt abban a geometriában, sem az algebrában, sem pedig még a számolás művészete sem volt elegendő annak megoldásához.

Euler úgy vélte, ez a probléma az volt kapcsolatos a téma, hogy Gottfried Wilhelm Leibniz volt egyszer megbeszéltük kíván dolgozni, valami Leibniz a továbbiakban geometria weboldal, vagy geometria helyzetbe. Ez az úgynevezett pozíciógeometria az úgynevezett gráfelmélet, amelyet Euler bevezet és használ a híres probléma megoldása során.

Euler igazolása

1735.augusztus 26-án Euler bemutatja a Konigsberg-híd problémájának megoldását tartalmazó papírt. Foglalkozik mind ezzel a konkrét problémával, mind pedig egy általános megoldással, tetszőleges számú terepjáróval, valamint tetszőleges számú híddal. Ez a “Solutio problematis ad geometriam situs pertinentis” című tanulmány 1741-ben jelent meg . Euler dolgozata huszonegy számozott bekezdésre oszlik, és a következőkben az Euler bekezdéseinek egyszerűsített változata kerül bemutatásra.

Euler bizonyításának első két bekezdésében bemutatja a Konigsberg-híd problémáját. Az (1) bekezdésben Euler kijelenti, hogy úgy véli, hogy ez a probléma a geometriára vonatkozik, de nem a kortársai által jól ismert geometriára, amely méréseket és számításokat foglal magában, hanem egy újfajta geometriára, amelyet Leibniz a pozíció geometriájának nevezett. Ezután a (2) bekezdésben Euler elmagyarázza közönségének, hogyan működik a Konigsberg probléma. Euler vázlatot adott a problémáról (lásd Euler 1. ábráját), és a hét különálló hidat nevezte meg: a, b, C, d, e, f és, g. ebben a bekezdésben kijelenti a probléma általános kérdését: “meg lehet-e tudni, hogy pontosan egyszer lehet-e áthaladni az egyes hídokon?”

Euler ‘s Figure 1 from” Solutio problematis ad geometriam situs pertinentis, ” Eneström 53

miután kijelentette Az általános kérdést, amelyet megpróbál megoldani, Euler elkezdi felfedezni a megoldás megtalálásának különböző módszereit. A (3) bekezdésben Euler elmondja az olvasónak, hogy ennek a konkrét problémának a megoldásához minden lehetséges utat leírhat, de ez a technika sok időt vesz igénybe, és nem fog működni nagyobb konfigurációkban, több hidakkal és földtömegekkel. E kérdések miatt Euler úgy döntött, hogy más módszert választ a probléma megoldására.

A (4) bekezdésben elkezdi egyszerűsíteni a problémát egy kényelmes rendszer feltalálásával, amely egy híd átkelését ábrázolja. Euler úgy dönt, hogy ahelyett, hogy a kisbetűket a híd átkelésének ábrázolására használná, a nagybetűket írja le, amelyek a földmaszkot képviselik. Például, hivatkozva a figura 1, AB jelentené utazás kezdődött landmass A, és véget ért B. Továbbá, ha utazás után landmass a B, valaki úgy dönt, hogy mozog landmass D, Ez egyszerűen jelölik, ABD. Az (5) bekezdésben Euler folytatja a folyamatról folytatott megbeszélését, elmagyarázva, hogy az ABDC-ben, bár négy nagybetűk vannak, csak három hidat kereszteztek. Euler elmagyarázza, hogy függetlenül attól, hogy hány híd van, lesz még egy levél, amely képviseli a szükséges átkelést. Emiatt a Königsberg – híd teljes problémája hét hidat kellett átlépni, ezért nyolc nagybetűt.

A (6) bekezdésben Euler folytatja módszerének részleteinek magyarázatát. Azt mondja az olvasónak, hogy ha egynél több híd van, amelyet át lehet lépni, amikor az egyik földről a másikra megy, akkor nem számít, melyik hídot használják. Például annak ellenére, hogy két híd van, az a és a b, amelyek egy utazót A-ból B-be vihetnek, nem számít Euler jelölésével, hogy melyik hidat veszik. Ebben a bekezdésben Euler azt is tárgyalja, hogy milyen konkrét problémával foglalkozik. Eredeti alakjával elmagyarázza, hogy a Königsberg-problémának pontosan nyolc betűre van szüksége, ahol az (A,B) és (a,C) pároknak pontosan kétszer kell megjelenniük egymás mellett, függetlenül attól, hogy melyik betű jelenik meg először. Ezenkívül a pároknak (a,D), (B,D) és (C, D) pontosan egyszer kell együtt fordulniuk egy olyan úthoz,amely egyszer és csak egyszer keresztezi az egyes hídokat, hogy létezzenek.

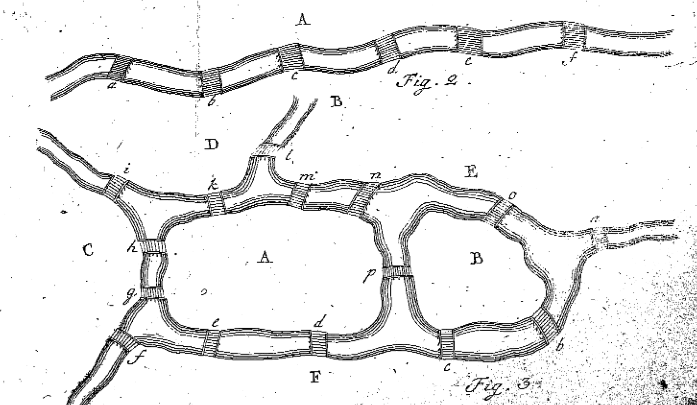
Euler ‘s Figures 2 and 3 from” Solutio problematis ad geometriam situs pertinentis, ” Eneström 53

A 7.bekezdésben Euler tájékoztatja az olvasót, hogy vagy meg kell találnia egy nyolcbetűs szekvenciát, amely kielégíti a problémát, vagy bizonyítania kell, hogy nincs ilyen szekvencia. Mielőtt ezt megtenné a Königsberg Hídprobléma miatt, úgy dönt, hogy talál egy szabályt annak felfedezésére, hogy létezik-e út egy általánosabb problémához. Ezt a 8.bekezdésben úgy teszi, hogy sokkal egyszerűbb példát mutat a földjárókra és a hidakra. Euler rajzolja a 2. ábrát, és elkezdi felmérni azokat a helyzeteket, ahol az a régió áthalad. Euler kijelenti, hogy ha az a hidat egyszer megtették, akkor az a volt az, ahol az utazás megkezdődött vagy véget ért, ezért csak egyszer használták. Ha az A, b és c hidak mind egyszer közlekednek, akkor az A-t pontosan kétszer használják, függetlenül attól, hogy a kiindulási vagy a befejező hely. Hasonlóképpen, ha öt híd vezet A-hoz, a landmass a pontosan háromszor fordul elő az utazás során. Euler kijelenti, hogy ” általában, ha a hidak száma páratlan szám, és ha az eggyel nő, akkor az a előfordulások száma az eredmény fele.”Más szóval, ha páratlan számú híd köti össze az a-T más terepjárókkal, adjon hozzá egyet a hidak számához, és ossza meg kettővel, hogy megtudja, hányszor kell A-t használni az ösvényen, ahol minden hidat egyszer és csak egyszer használnak (azaz Összesen előfordulások egy, ahol egy páratlan # hidak = (#hidak-1) / 2).

ezzel a ténnyel Euler megoldja a Königsberg-híd problémáját a 9. bekezdésben. Ebben az esetben, mivel öt híd vezet A-hoz, háromszor kell megtörténnie (lásd a fenti 1.ábrát). Hasonlóképpen, a B, C és D-nek kétszer is meg kell jelennie, mivel mindegyiknek három hídja van, amelyek hozzájuk vezetnek. Ezért 3 (A) + 2 (B) + 2(C) + 2 (D) = 9, de Euler már kijelentette, hogy a hét híd esetében csak nyolc előfordulás lehet. Ez ellentmondás! Ezért lehetetlen a hidakat Königsberg városában egyszer csak egyszer utazni. A vége, vagy az? Bár Königsberg népe elégedett lehet ezzel a megoldással, a nagy matematikus, Leonhard Euler nem volt elégedett. Euler tovább folytatja bizonyítékát az általánosabb helyzetek kezelésére.

Euler általánosítása

a 10. bekezdésben Euler folytatja a vitát azzal, hogy megjegyzi, hogy ha a helyzet minden furcsa számú híddal rendelkező földjárót magában foglal, meg lehet mondani, hogy egy utazás csak egyszer lehetséges-e minden híd használatával. Euler kijelenti, hogy ha az egyes betűk számának összege még egy, akkor a hidak teljes száma, Egy utazás elvégezhető. Ha azonban az események száma egynél több, mint a hidak száma, akkor nem lehet utazni, mint például a Königsberg-híd problémája. Ez azért van, mert az a szabály, amelyet Euler páratlan számú hidat ad, a 2.ábráját használva, igaz az általános helyzetre, hogy csak egy másik szárazföldi vagy egynél több van-e.

A 11.és 12. bekezdésben Euler foglalkozik azzal a helyzettel, amikor egy régióhoz páros számú híd kapcsolódik. Ez a helyzet nem jelenik meg a Königsberg-problémában, ezért eddig figyelmen kívül hagyták. Abban a helyzetben, amikor a landmass X páros számú hidat tartalmaz, két eset fordulhat elő. Az első eset az, amikor X az utazás kiindulópontja. Ebben az esetben az X kétszer jelenik meg, egyszer kiindulási pontként, majd ismét végpontként. A másik esetben az X nem a kiindulási pont. Ha ez megtörténik, X csak egyszer jelenik meg, mivel az utazásnak az egyik hídon keresztül kell belépnie, és azonnal el kell hagynia az egyetlen rendelkezésre álló másikon keresztül. Hasonlóképpen, ha az X-hez négy híd van csatlakoztatva, az X előfordulásainak száma attól függ, hogy kiindulási pont-e vagy sem. Ha az utazás X-ben kezdődik, akkor háromszor kell megjelennie, de ha nem kezdődik X-ben, akkor csak kétszer jelenik meg. Tehát általában, ha X páros számú hidat csatol, akkor ha az utazás nem indul el X-ben, akkor X a hidak számának felével jelenik meg (azaz Előfordulások X ahol X egyenletes, nem pedig a kiindulási pont = (#hidak) / 2). Ha az út X-ben indul, akkor X feleannyi alkalommal jelenik meg, mint hidak, plusz egy (azaz X olyan eseményei, ahol X páros és kiindulási pont = ((hidak száma) / 2) + 1).

a 13-15. bekezdésben Euler elmagyarázza, hogyan lehet kitalálni, hogy létezik-e egy útvonal, amely minden hídot egyszer és csak egyszer használ, és bemutatja saját példáját, hogy megmutassa, hogyan működik. Euler először elmagyarázza egyszerű, hatlépcsős módszerét, hogy megoldja az általános helyzetet a folyókkal megosztott és hidakkal összekapcsolt földmaszk esetén. Első Euler jelöli minden landmass nagybetűvel. A második, hogy elveszi a hidak teljes számát, hozzáad egyet, és ezt a diagram fölé írja, amelyet hamarosan elkészít. Ezután veszi a nagybetűket, oszlopba helyezi őket, mellette pedig a hidak számát írja. Negyedszer csillagokkal jelzi azokat a földmérőket, amelyek páros számú hidat tartalmaznak. Ezután minden páros szám mellett ½ – t ír a számból, majd minden páratlan szám mellett ½ – t helyez el a szám plusz egy. Végül Euler hozzáadja a jobb oldali oszlopban írt számokat, és ha az összeg egy kisebb, vagy azzal egyenlő, a hidak száma plusz egy, akkor a szükséges utazás lehetséges. Fontos azonban megjegyezni, hogy ha az összeg egy kisebb, mint a hidak száma plusz egy, akkor az utazásnak a csillaggal jelölt földmérők egyikéből kell indulnia. Ha az összeg megegyezik a hidak számával plusz egy, az utazásnak csillaggal nem jelölt régióban kell kezdődnie.

példák

a Konigsberg probléma első példájaként Euler a következőket mutatja:

hidak Száma = 7, hidak Száma plusz egy fő = 8

Régió Hidak Alkalommal Régió fel Kell tüntetni

5 3

B 3 2

C 3 2

D 3 2

Azonban, 3 + 2 + 2 + 2 = 9, ami több, mint 8, szóval az út lehetetlen.

mivel ez a példa meglehetősen alapvető, Euler úgy dönt, hogy saját helyzetét két szigettel, négy folyóval és tizenöt híddal tervezi meg. Az Euler által létrehozott helyzet a fenti 3. ábrán látható. Euler most megpróbálja kitalálni, hogy van-e olyan út, amely lehetővé teszi, hogy valaki csak egyszer menjen át minden hídon. Euler a következő módon ugyanazokat a lépéseket, mint a fenti, elnevezése az öt különböző régiók nagybetűkkel, majd létrehoz egy táblázatot, hogy ellenőrizze, ha lehetséges, mint a következő:

hidak Száma = 15, Hidak száma plusz egy = 16

Régió Hidak Alkalommal Régió fel Kell tüntetni

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

ezen kívül, 4 + 2 + 2 + 2 + 3 + 3 = 16, ami egyenlő a hidak száma, plusz egy fő, ami azt jelenti, hogy az út, sőt, lehetséges. Mivel az összeg megegyezik a hidak számával plusz egy, az utazásnak D-ben vagy e-ben kell kezdődnie. Most, hogy Euler tudja, hogy lehetséges egy utazás, csak annyit kell tennie, hogy meghatározza, mi lesz az út. Euler kiválasztja az eafbbcfdaeffcgahcidkamenapboeld utat, ahol magában foglalja, hogy mely hidakat keresztezik a földmérőket ábrázoló betűk között. Bár ez az információ idegen, mivel a pontos híd nem számít annak tudatában, hogy egy utazás lehetséges, hasznos az út kiválasztásakor. Ez egy jó példa, amely megmutatja azt a módszert, amelyet Euler használna az ilyen jellegű problémák megoldásakor.

Euler következtetései

a következő néhány bekezdésben az Euler egy másik módszert mutat be annak kiderítésére, hogy lehet-e utazni bármilyen szárazföldi út, híd és folyó esetén. A 16. bekezdésben Euler rámutat arra, hogy a közvetlenül a földutak jobb oldalán felsorolt számok összessége a hidak teljes számának kétszeresét teszi ki. Ez a tény később a kézfogás lemma néven ismert. Alapvetően a kézfogás lemma azt állítja, hogy minden hídot kétszer számítanak, egyszer minden olyan földmaszkhoz, amelyhez csatlakozik. A 17. bekezdésben Euler kijelenti, hogy az egyes régiókhoz vezető összes híd összege egyenletes, mivel ennek a számnak a fele megegyezik a hidak teljes számával. Ez azonban lehetetlen, ha páratlan számú, páratlan számú híddal rendelkező földmaszk van. Ezért Euler bizonyítja, hogy ha van néhány páratlan szám a földtömegekhez, akkor ezeknek a földmérőknek páros számúnak kell lenniük.

Ez azonban nem elegendő annak bizonyítására, hogy van-e olyan út, ahol minden hidat egyszer és csak egyszer használnak, mivel a Königsberg-híd problémájának páros száma van, páratlan számú híddal. Emiatt az Euler További korlátozásokkal egészíti ki a 18.és 19. bekezdést. Euler elmagyarázza, hogy mivel az egyes földmaszkhoz csatolt hidak számának összege megegyezik a hidak számának kétszeresével (amint az a kézmozgató lemma-ban látható), ezért ha kettőt ad hozzá ehhez az összeghez, majd kettővel oszd meg, akkor a teljes hidak számát plusz egy. Ez a szám ugyanaz, mint az előző, amelyet arra használnak, hogy megmondják, lehetséges-e egy útvonal. Ha az összes szám egyenletes,akkor a táblázat harmadik oszlopa eggyel kevesebb, mint a hidak száma plusz egy.

Euler ezután kifejti, hogy nyilvánvaló, hogy ha két, páratlan számú híddal rendelkező földút van, akkor az utazás mindig lehetséges, ha az utazás az egyik régióban páratlan számú híddal kezdődik. Ennek oka az, hogy ha a páros számok felére csökkennek, és a páratlan számok mindegyikét egyvel növelik és felére csökkentik, akkor ezeknek a feleknek az összege eggyel több lesz, mint a hidak teljes száma. Ha azonban négy vagy több földút van páratlan számú híddal, akkor lehetetlen, hogy legyen egy út. Ennek oka az, hogy a páratlan számok feleinek összege plusz egy a páros számok összes felének összegével együtt a harmadik oszlop összege nagyobb lesz,mint a hidak teljes száma plusz egy. Ezért Euler csak bebizonyította, hogy legfeljebb két földút lehet páratlan számú híddal.

ezzel kijelentve, Euler most következtetéseket vonhat le a Königsberg-híd problémájának általánosabb formáiról. A (20) bekezdésben az Euler megadja azt a három iránymutatást, amelyet valaki használhat annak kiderítésére, hogy létezik-e út minden híd használatával egyszer és csak egyszer. Először azt állította, hogy ha több mint két landmasses van páratlan számú hidakkal, akkor ilyen utazás nem lehetséges. Másodszor, ha a hidak száma páratlan pontosan két landmasses, akkor az utazás lehetséges, ha indul az egyik a két páratlan számozott landmasses. Végül, Euler kijelenti, hogy ha nincsenek olyan régiók, ahol páratlan számú földút van, akkor az utazás bármely régióban megkezdhető. E három tény megállapítása után Euler a 21. bekezdéssel zárja le bizonyítékát, amely egyszerűen kimondja, hogy miután az egyik kitalálja, hogy létezik egy út, még mindig meg kell haladniuk az erőfeszítéseket, hogy leírják a működő utat. Euler úgy vélte, a módszer ennek megvalósítására triviális, és nem akar sok időt tölteni rajta. Euler azonban azt javasolta, hogy összpontosítson arra, hogyan juthat el az egyik földmaszkból a másikba, ahelyett, hogy először a konkrét hidakra koncentrálna.

Euler Bizonyíték, valamint Gráf Elmélet

olvasva Euler eredeti bizonyíték, feltűnik egy viszonylag egyszerű, könnyen érthető munka matematika; ez azonban nem a tényleges bizonyítékot, de a köztes lépéseket, hogy ez a probléma híres. Euler nagy újítása az volt, hogy a Königsberg-híd problémáját elvontan szemlélte, vonalak és betűk segítségével ábrázolta a földmaszkok és hidak nagyobb helyzetét. Nagybetűkkel ábrázolta a földmaszkot, kisbetűkkel pedig hidakat ábrázolt. Ez egy teljesen újfajta gondolkodásmód volt, és Euler a dolgozatában véletlenül egy új matematikai ágat, a gráfelméletet hozta létre, ahol a gráf egyszerűen csúcsok és élek gyűjteménye. Ma egy gráfban egy görbét, amely a gráf minden szélét egyszer és csak egyszer tartalmazza, Euler-görbének nevezzük, e probléma miatt. Attól az időtől kezdve, amikor Euler megoldotta ezt a problémát a mai napig, a gráfelmélet a matematika fontos ágává vált, amely a hálózatokra való gondolkodásunk alapját irányítja.

a Königsberg – híd problémája az, hogy a Biggs miért állítja,

a gráfelmélet eredete szerény, sőt komolytalan … a gráfelmélet kialakulásához vezető problémák gyakran alig voltak több, mint rejtvények, amelyek célja a találékonyság tesztelése, nem pedig a képzelet ösztönzése. De az ilyen rejtvények látszólagos trivialitása ellenére megragadták a matematikusok érdeklődését, azzal az eredménnyel, hogy a gráfelmélet meglepő változatosság és mélység elméleti eredményeiben gazdag témává vált.

mivel a Biggs nyilatkozata azt jelentené, ez a probléma annyira fontos, hogy minden gráfelméleti könyv első fejezetében megemlítik, amelyet a könyvtárban használtak.

Euler felfedezése (vagy találmánya, attól függően, hogy az olvasó hogyan néz ki) után a gráfelmélet olyan nagy matematikusok jelentős hozzájárulásaival virágzott, mint Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff és George Polya. Ezek az emberek mind hozzájárultak ahhoz, hogy felfedezzék ” szinte mindent, ami a nagy, de rendezett grafikonokról ismert, mint például a kristályban lévő atomok által alkotott rács vagy a méhek által méhkaptárban készített hatszögletű rács .”Más híres gráfelméleti problémák közé tartozik megtalálni a módját, hogy elkerülje a labirintus vagy labirintus, vagy megtalálni a sorrendben mozog egy lovag egy sakktábla úgy, hogy minden téren leszállt csak egyszer, és a lovag visszatér a tér, amelyen elkezdte . Néhány más gráfelméleti probléma évszázadok óta megoldatlan .

Königsberg sorsa

míg a gráfelmélet fellendült, miután Euler megoldotta a Königsberg-híd problémáját, Königsberg városának sokkal más sorsa volt. 1875-ben Königsberg lakói úgy döntöttek, hogy új hidat építenek a B és C csomópontok között, ezzel négyre növelve e két földút összeköttetéseinek számát. Ez azt jelentette, hogy csak két landmasses volt páratlan számú linkek, amely adott egy meglehetősen egyszerű megoldás a problémára. Az extra híd létrehozását tudat alatt okozhatta vagy nem okozhatta a város híres problémájának megoldására szolgáló út vágya.

azonban egy új híd nem oldotta meg Königsberg összes jövőbeli problémáját, mivel a város nem számított vissza a tizenkilencedik században ” a szomorú és háború sújtotta sors, amely a második világháború egyik legvadabb csatájának házigazdájaként várta.”1944 augusztusában négy nap alatt a brit bombázók elpusztították mind az óvárost, mind Königsberg északi részét. 1945 januárjában és februárjában a Königsberget körülvevő területet orosz erők veszik körül. A német civilek elkezdenek evakuálni a városból, de túl későn mozognak. Több ezer ember hal meg, miközben hajóval próbálnak elmenekülni a Curonian lagúna jeges vizein. 1945 áprilisában a Vörös Hadsereg elfoglalja Königsberget az óváros mintegy kilencven százalékával, amely romokban hever.

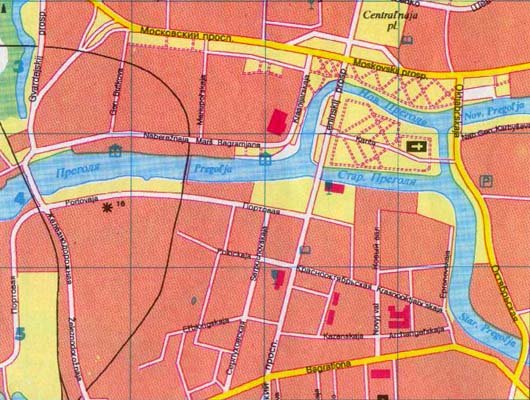
Königsberg jelenlegi utcatérképe az alábbiakban található . Ez a térkép megmutatja, hogy a város mennyit változott. A bombázások során sok híd megsemmisült, és a város már nem kérdezheti meg ugyanazt az érdekes kérdést, amelyet a tizennyolcadik században tudtak. A Königsberg városának egy nagyon eltérő elrendezése mellett új neve van, Kalinyingrád, a Pregel folyó pedig Pregolya. Míg Königsberg sorsa szörnyű, a polgárok régi kávéházának problémája, hogy pontosan egy időben áthaladtak a régi hét hídján, a matematika teljesen új ágának, a gráfelméletnek a kialakulásához vezetett.

Biggs, Norman L., E. K. Lloyd és Robin J. Wilson. Gráfelmélet: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Euler: mindannyiunk mestere. Washington: Az Amerikai Matematikai Egyesület 1999.

Euler, Leonhard, “Solutio problematis ad geometriam situs pertinentis” (1741), Eneström 53, MAA Euler Archive.

“History of Mathematics: On Leonhard Euler (1707-1783).”ScienceWeek (2003). November 6. 2005.

Hopkins, Brian és Robin Wilson. “Az igazság Königsbergről.”College Mathematics Journal (2004), 35, 198-207.

” Konigsberg.”The MacTutor History of Mathematics Archive:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

szerkesztő megjegyzése: Ez a cikk eredetileg megjelent konvergencia, kötet 3 (2006).