A Négy Szín Tétel
A Négy Szín Sejtés volt az első kijelentette, több mint 150 évvel ezelőttről, végül bizonyította meggyőzően 1976-ban. Ez egy kiemelkedő példa arra, hogy a régi ötletek hogyan kombinálódnak az új felfedezésekkel éstechnikákat a matematika különböző területein, hogy újakat biztosítsanak egy probléma megközelítéséhez. Ez is egy példa arra, hogy egy látszólag egyszerű problémát “megoldottnak” gondoltak, de aztán egyre több lett, és ez az első látványos példa, amikor egy számítógép részt vett egy matematikai tétel bizonyításában.
az elején
az a feltételezés, hogy bármely térkép csak négy szín felhasználásával színezhető, először egy levélben jelent megaugustus De Morgan (1806-1871), a matematika első professzora A new University College London, barátjának, William Rowanhamiltonnak (1805-1865), a híres ír matematikus 1852-ben. Azt javasolta, hogy De Morgan az egyik tanítványa, FrederikGuthrie, nevében bátyja Francis (aki később lettprofesszora matematika a University of Cape Town).


Augustus De Morgan (1807-1871) éswilliam Rowan Hamilton (1805-1865)
a probléma, így egyszerűen leírva, de annyira tantalizingly nehézhogy bizonyítani, elkapta a képzelet sok matematikus idején. Az 1860-as évek végén De Morgan még Amerikába is eljutott, ahol többek között Benjamin Peirce (1809-1880) neves matematikus és csillagász is érdeklődött iránta, hogy miként fejlesztheti logikai módszereit.
De Morgan azt a tényt használta, hogy egy négy régióval rendelkező térképen mindegyik a másik háromhoz tartozik, ezek közül az egyiket teljesen bezárják a többiek. Mivel ezt nem tudta bizonyítani, axiómaként használta, a bizonyíték alapja.
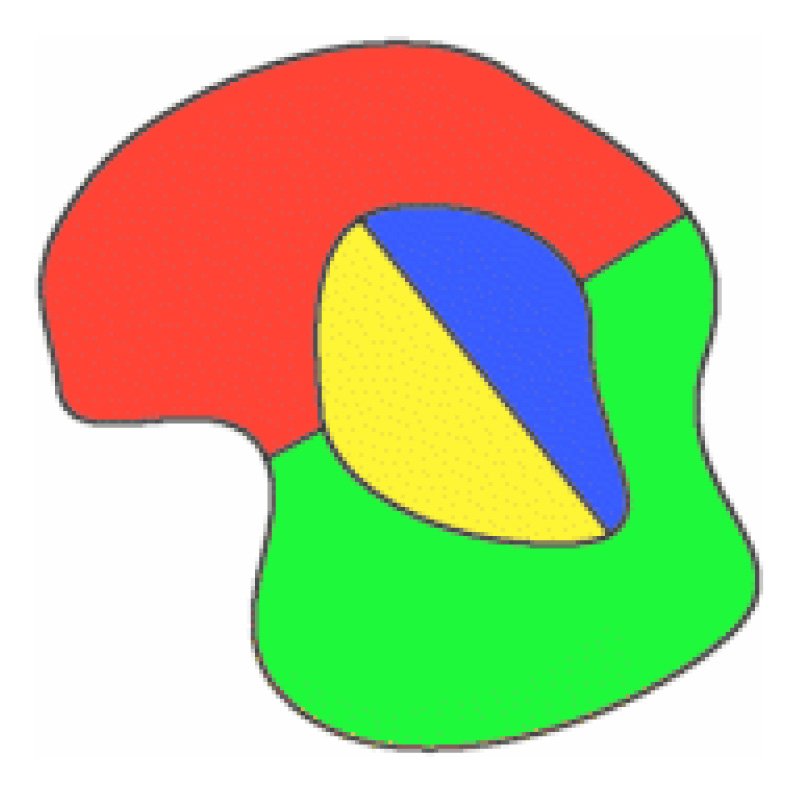
De Morgan originalsketch másolata a Hamiltonnak írt levelében és egy egyszerű négyszínű térkép.
1878-ban Arthur Cayley (1821-1895) a Londoni Matematikai Társaság ülésén megkérdezte, hogy valaki megtalálta-e a megoldást forDe Morgan eredeti kérdésére, de bár volt valami érdekes, senki sem tett jelentős előrelépést. Cayley lett érdekelt a probléma, és 1879-ben megjelent egy rövid paperOn a színezés mapswhere elmagyarázta néhány nehézséget próbál bizonyítékot, és tett néhány fontos hozzájárulást, hogy a probléma megoldott. Arra a kérdésre, hogy ” ha egy adott térkép már négy színnel van színezve, és hozzáadunk egy másik területet, megtarthatjuk-e még ugyanazt a színezést?””egy másik, a probléma matematikai értelmezését lehetővé tévő vonal indult el.

Arthur Cayley (1821-1895)
Arthur Cayley megmutatta, hogy ha már négyszínt használtak a térkép színezésére, és egy új régiót adtak hozzá, akkor nem mindig lehetett megtartani az eredetitfestés.
Az eredeti térképen mind a négy színt felhasználták,és egy új régiót rajzoltak köré. Ebben az esetben egy vörös régió vankékre változott, így a piros használható az új környezetbenrégióban.
Cayley azt is megfigyelte, hogy a probléma egy változatát a határok teljesülésének korlátozásával lehet megoldani. Például azok a térképek, ahol csak három ország találkozott, három éllel találkoznak az avertex-en. Ezeket “köbös térképeknek” nevezik, és a következő vitában használt térképek mind köbös térképek. Továbbá, ha egy térkép négy színnel színezhető, akkor csak három szín jelenik meg a határon.
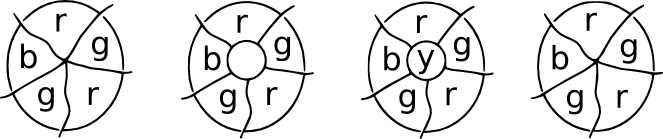
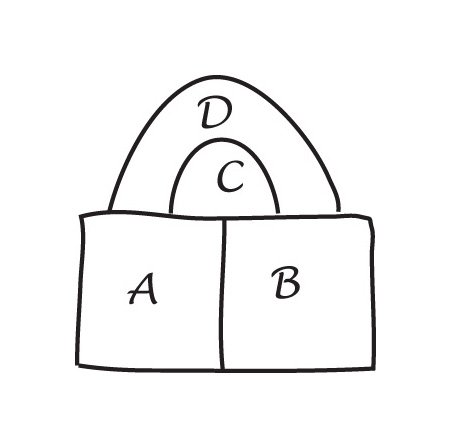
a Patch bemutató. Képzeld el, hogyegy helyen egy térképen számos ország találkozik egy ponton. Most a találkozási pont fölé helyezünk egy foltot,és az összes új találkozási pontnak három határa lesz. Ezek köbös térképek, és egy negyedik szín használható a központi régió számára. A tapasz eltávolításakor visszatérhetünk az eredeti színezéshez.
néhány régi technika, új feltételek és még több probléma!
a probléma fejleményeinek nyomon követéséhez röviden meg kell vizsgálnunk azokat az elképzeléseket, eljárásokat és technikákat, amelyeket a matematikusok a megoldási kísérleteik során fejlesztettek ki.
az egyetlen öt szomszéd sejtése
” Ha nem tudja megoldani az apartikuláris problémát, keressen egy könnyebb megoldást.”(Polya. Hogyan oldjuk meg)
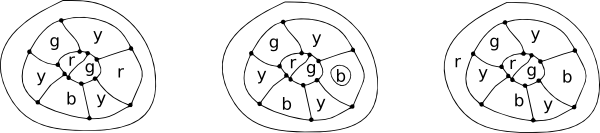
” minden térképen legalább egy ország van öt vagy kevesebb szomszéddal.”
Képzeljünk el egy térképet egy sziget körül a tenger. A szigetországok színeiben a tengert egynek tekintjük. Néhány országnak csak két határa lehet( egy digon), néhányhárom (mint egy háromszögben), néhány Négy (egy négyzet) és néhány öt (apentagon)vagy több.
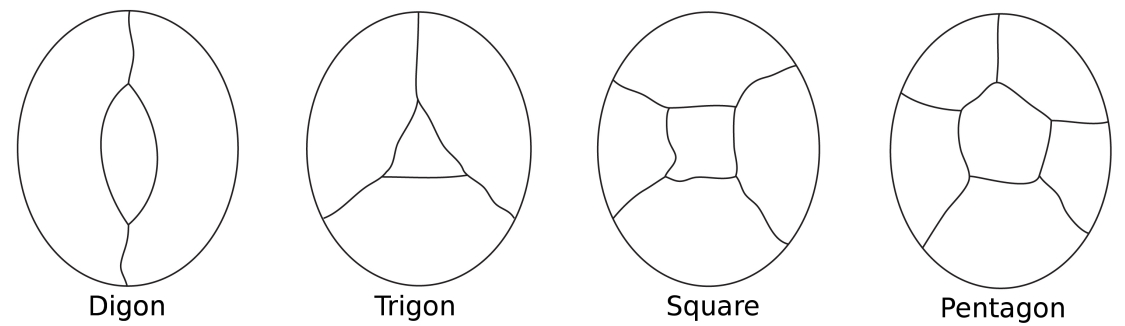
a lehető legegyszerűbbkonfigurációk egy központi régió körül.
vegye figyelembe, hogy az összes ilyen konfigurációban minden csomópontnak csak három vanges.
1813-ban Euler poliéderre vonatkozó képletét Augustin Cauchy (1759-1857 Ily módon a képlet $F + V – e = 1$ lett, merta Cauchy nem számolta a nettó “külső” régiót.

Augustin Cauchy (1759-1857)
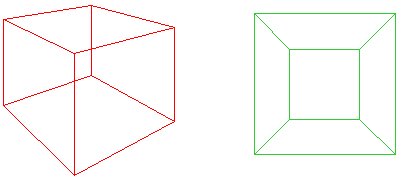
Képzeld el, squashing a piros kocka downonto egy gépet úgy, hogy a bázis nyitotta ki, hogy létrehozzák a outsideedge a zöld net. Cauchy ötlete az volt, hogy kivágja a kocka egyik arcát, hogy egy sík sokszög esetén $F + v – e = 1$. Alternatív megoldásként,ha a “külső”, a nettó tekinteni, mint egy arc, infinitearea, akkor még van $f + v – e = 2$
feltételezhetjük, hogy legalább három határon vonalak (élek), a feltörekvő az egyes találkozási pont (pontok).
annak bizonyítéka, hogy a térképen legalább egy ország van, amelyet öt vagy kevesebb szomszéd vesz körül. Ha ez abszurditáshoz vezet, van bizonyítékunk.
most tegye ezeket az értékeket Euler képletébe: $$F + V-e = 2$ $ andwe have $$1/3 (e) + 2/3(e) – E$$ which is zero!
Ez az abszurditás, tehát eredeti feltételezésünk hamis volt.Ez azt jelenti, hogy legalább egy országnak kell lennie öt vagy kevesebb szomszéddal!
minimális bűnözők!
a négyszínes probléma megoldásának másik módja az, ha azt feltételezzük, hogy ez nem megfelelő, és meglátjuk, hogy ez hova vezet. Tegyük fel, hogy vannak olyan térképek, amelyekre szükség vanöt vagy több szín, és a térképeket a lehető legkisebb számú országgal választjuk ki. Ezeket a térképeket minimális ellenpéldáknak vagyminimális bűnözők !
tehát ez azt jelenti, hogy egy minimális bűnözőt nem lehet négy színnel színezni, de minden kevesebb országú térképet négy színnel lehet színezni. Ha meg tudjuk mutatni, hogy minimális bűnözők nem létezhetnek, akkor talán tudunk előrelépni.
például megmutathatjuk, hogy egy minimális bűnöző nem tartalmazhat digont.
az eredeti térképről, távolítson el egy határt a digontól, ésegy új térképet kapunk kevesebb országgal. Ez a térkép négy színnel színezhető (feltételezésünk szerint). Ezután színezzük ezt az új képet (csak két színre van szükségünk). Most cserélje ki az eltávolított szegélyt, majd színezze újra a térképet. Három színt használtunk, és mivel thereis még egy szín áll rendelkezésre, ez azt mutatja, hogy térképünk négy színnel színezhető. De ez ellenkezik a feltételezésünkkel, így egy minimális bűnöző nemtartalmaz egy digont.
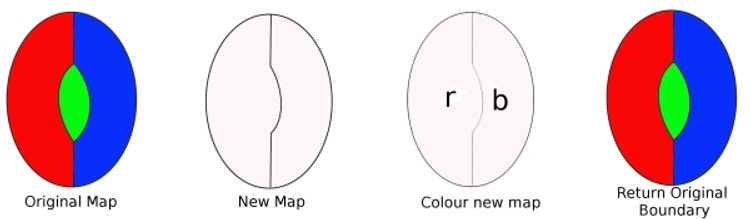
annak bizonyítására, hogy a minimális Kriminalcannot két élű régiót (a digon) tartalmaz. Tegyük fel, hogy vanegy minimális bűnöző, amely digont tartalmaz. Az él eltávolítása azt jelentia térkép kevesebb régiót tartalmaz. Tehát ez az új térkép négy színnel színezhető. Most cserélje ki az elveszett él. Mivel korábban csak két színre volt szükség, az él cseréje azt jelenti, hogy használhatjuk a harmadik színt, és még mindig van egy negyedik szín, amelyet használhatunk. Tehát egy minimálisbűnözőt négy színnel lehet színezni. Ezért a minimális criminal nem tartalmazhat digont.
Ez az eljárás megismételhető annak bizonyítására, hogy egy minimális kriminálisnem tartalmaz egy háromoldalas országot (trigon), de lebomlikamikor a technikát egy négyzeten próbáljuk meg, mert amikor helyettesítjük a négyzetet, a mellette lévő országok mind a négy színt használhatják, így a bizonyítási eljárás sikertelen. Amint ez megtörtént, nyilvánvalóvá válik, hogy nem fog működni a pentagonok számára, stb.
The Six Colour Theorem
hasonló technikával lehet kimutatni, hogy a hat színtéma igaz. Először is feltételezzük, hogy nincsenek olyan térképek, amelyek lehetnekszínezett hat színnel. A térképek egy része egyenletes színekkel is színezhető, így ha egy ilyen (minimális bűnöző) közül választunk egyet, ha megmutatjuk, hogy kevesebb mint hét színnel lehet színezni, akkor elértük a célunkat.
az öt szomszéd-tétel bizonyításából az is kiderül, hogy a minimális bűnötlet segítségével minden térkép színezhető hatszínnel!
A Régiók Csomó, Hálózatok, Topology
1879-Ben Alfred Kempe (1849-1922), technikák alkalmazásával, hasonló tothose a fent leírt, kezdve a ‘öt szomszédok ingatlan’and kifejlesztett egy eljárást, ismert, mint a módszer ‘Kempe Láncok’ tofind egy igazolást a Négy Szín Tétel. Ezt a bizonyítékot közzétetteaz American Journal of Mathematics. Két egyszerűbb változatot talált, amelyek a következő évben jelentek meg, és bizonyítása tíz évig állt, mielőtt Percy Heawood (1861-1955) megmutatta, hogy súlyos hiba történt a Kempe által alkalmazott bizonyítási módszerben.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) és Percy heawood (1861-1955)
1880-ban P. G. tait (1831-1901) matematikai fizikus, a probléma megoldására. Függetlenül attól, hogy Tait megállapította, hogy a térképeket, ahol minden ponton páros számú határvonal találkozik, két színnel lehet színezni, bár ez az eredmény korábban megjelent Kempe papírjaiban.
során 1876-77 Tait vált ismertté a tanulmány ésosztályozása csomók. Abban az időben számos voltkülönböző elméletek az atomok szerkezetéről. William Thompson (később Lord Kelvin 1824-1907) Hermann von Helmholtz (1821-1894) német fizikus kísérletei által inspiráltaz Atom csomózott csövek éterből. Kelvin elméletét a “Vortex atomokról” körülbelül húsz éven át komolyan vették, és arra ösztönözte Tait-ot, hogy végezze el a csomók osztályozását. Tait, Thomsonés James Clark Maxwell (1831-1879) számos topológiai ötletet talált fel tanulmányaik során. Kelvin elmélete azonban alapvetőenés a fizikusok elvesztették érdeklődését Tait munkája iránt.


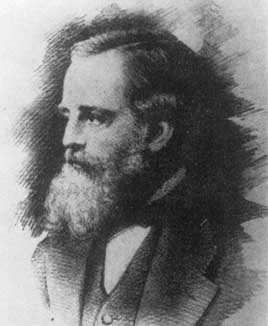
Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) és James Clark Maxwell (1831-1879)

h5 > tait kezdődött a módszereket, amelyek asingle zárt hurok zsinór lehet csomózott. Eleinte nem volt szisztematikusmódszere, és intuitív módon kezdett hozzá az asingle zárt hurokhoz, és kísérletezett azzal, hogy milyen módon lehet csomózni. Természetesen a zsinór nyitva volt (mint ashoelace), majd csomózott, majd csatlakozott. Vegye figyelembe, hogy ha követi a csomópontot, akkor a “túl aluljáró” kereszteződések váltakoznak.Ezután két hurokkal kísérletezett, és azt is, hogy milyen módon lehet őket összekötni. Itt látható a legfeljebb hat csomóegy hurok keresztezése.
Tait tanulmányának egyik eredménye a Hamiltoni gráf-sejtés volt.
egy térképet egy gömbre rajzolt poliédernek tekintünk,amelyet egy síkra vetíthetünk. Tait javasolta, hogy minden kubikuspolyhedral térkép Hamiltoniancycle . Tait módszere a grafikon széleire összpontosított ésmegmutatta, hogy egy Hamiltoni ciklus négy színező ofa térképet hozhat létre. William Tutte (1917-2002) csak 1946-ban találta meg Tait sejtésének első ellenpéldáját.
Tait a kapcsolatot csomó
Taitinitiated a tanulmány snarks 1880-ban, amikor bebizonyította, hogy a fourcolour tétel volt egyenértékű nyilatkozatot arról, hogy snark isplanar. A síkgráf olyan, amelyet a síkban lehet rajzolninincs élek átkelése. Úgy tűnik, hogy Tait ötlete a nem sík gráfokról a csomók és a Hamiltoni utak tanulmányozásából származik .
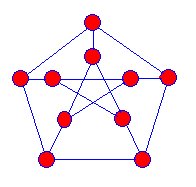
az első ismert snark az 1898-ban felfedezett Petersen-gráf volt,és a matematikusok több ilyen típusú grafikát kezdtek vadásznide csak 1946-ban találtak egy másik snarkot.
 |
|
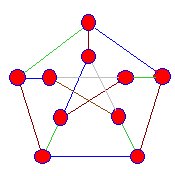 |
A szélek találkozó a csúcsa ez a snark színes, kék,zöld, barna, de mindig eléri azt a szintet, ahol ez a processcannot kell folytatni. |
Julius Peterson (1839-1910)
a hunting of thesnark egy Lewis Carroll által írt vers, Martin Gardner pedig ezeket a grafikonokat snarks-nak nevezte, mert annyira megfoghatatlanok voltak.
A probléma átalakítása és új módszerek megtalálása.
bár Heawood 1890-ben megtalálta Kempe bizonyítási módszerének legnagyobb hibáját, nem tudta bizonyítani a négy színtételét, de jelentős áttörést ért el, és meggyőzően bizonyította, hogy minden térkép öt színnel színezhető.
Heawood számos fontos hozzájárulást tett a problémához,áthelyezve a figyelem középpontját a térkép területeiről a köztük lévő határokra. 1898-ra bebizonyította,hogy ha az egyes régiók körüli területek száma 3-mal osztható, akkor a régiók négy színnel színezhetők.
Cauchy bizonyítéka az Euler-formula is tartalmazza az ötlet thatany nettó egy poliéder lehet háromszög hozzáadásával élek, hogy makenon-háromszög alakú arc a háromszögek. Ezután kidolgozott egy eljárást, amellyel egyenként törölte a széleket, megmutatva, hogy Euler formuláját minden lépésben meg lehet őrizni.
Cauchy Euler képletének igazolása
Cauchy 1813-as bizonyítéka Euler képletének azzal a gondolattal kezdődött, hogy egy poliéder aprojekciót kap egy síkhálóhoz. Hozzátette :a) minden hálót meg lehet háromszögelni, és Euler képletének bizonyítékát(b) akkor elfogadták.
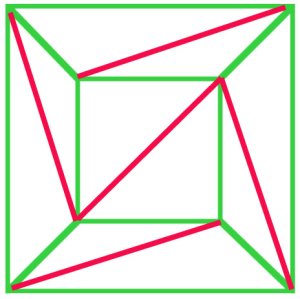 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
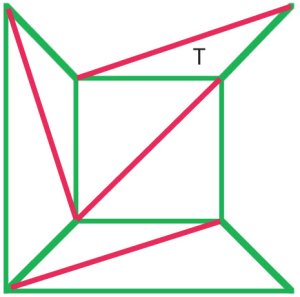 (b)
|
Cauchy érvelése az volt, hogy távolítsa el a külső széleket ábra(a) egyenként, majd amikor elérte a színpadon, mint az ábra (b)eltávolították az egész háromszög T, így megőrizve Euler-formula. A tizenkilencedik század eleji manymatematikusok egyetértettek abban, hogy ezaz eljárás bizonyította Euler képletét az allpolyhedra számára. |
1900-ra a matematikusok tudták, hogy a síkgráf bármely térképből átalakítható a dualitás erőteljes fogalmával . A duális, théregionok által képviselt csúcsok és két csúcsok vannak összekötve byan él, ha a régiók szomszédos. Ezekben a grafikonokban a négyszínes sejtés most azt kérdezi, hogy a gráf csúcsai 4 színnel színezhetők-e úgy, hogy két szomszédos csúcs ne legyen azonos színű.
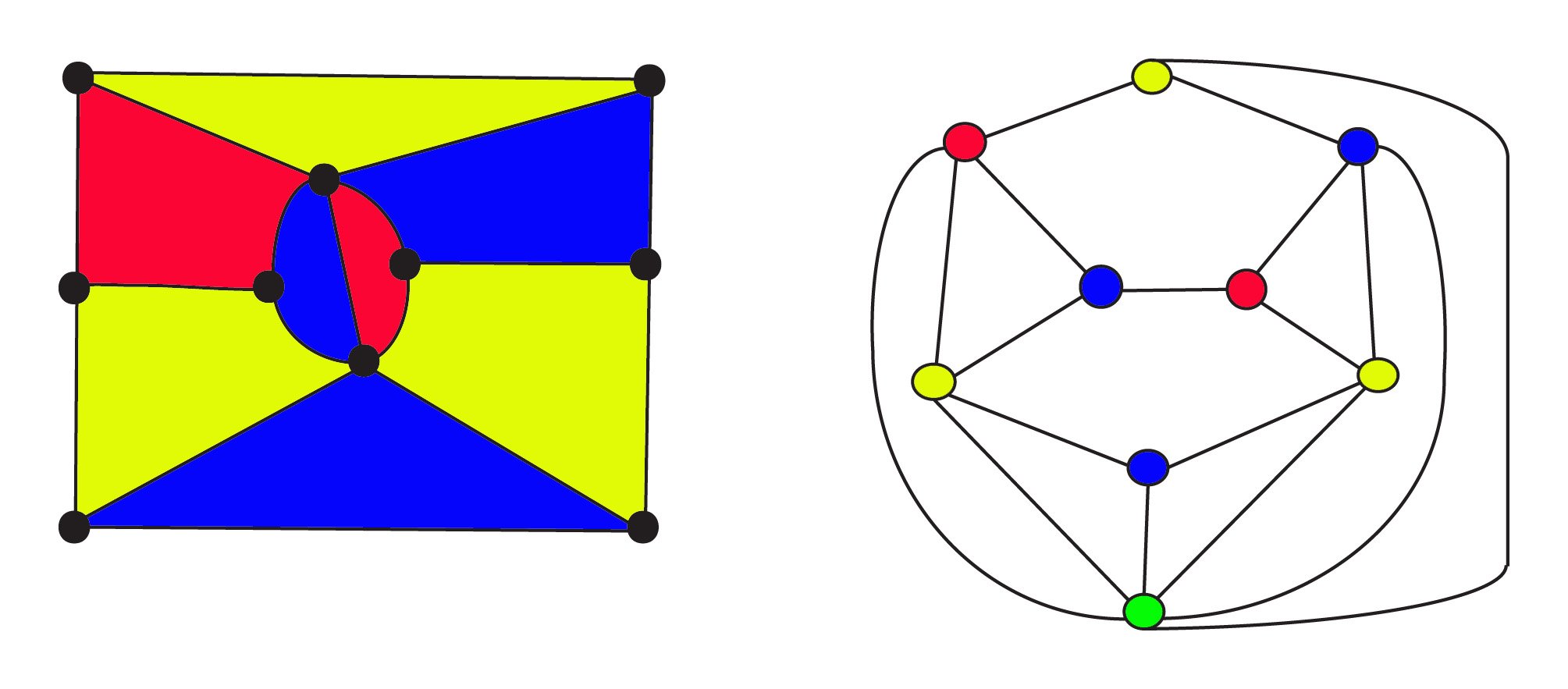
a bal oldali 3 színű térképen$8$-os régiók $10$ csúcsok és $17$ élek. A kettős gráfon $ 9 $ 9 $ 9 $ és $17$ élek vannak, ahol a csúcsok színezése megegyezik a térkép területeivel. A gráf alján található greenvertex a térkép végtelen külső területét képviseli. Mind az eredeti térkép, mind a kettős obey Euler ‘ sformula hálózatokhoz $ F + v-e = 1$ vagy, $ \ text{regions} + \ text{vertices} – \ text{élek} = 1$. A kettősség relációja issymmetric: a kettős kettős az eredeti gráf lesz, ahol a csúcsokat és a csúcsokat cserélik.
első felében a huszadik század, mathematiciansfocused a módosító ezeket a technikákat, hogy reducecomplicated térképek speciális esetekben, amely azonosítható andclassified, hogy vizsgálja meg az adott tulajdonságok anddeveloped az ötlet, hogy egy minimális készlet map konfigurációk, ez vizsgálni.
először azt hitték,hogy a készlet közel 9000 tagot tartalmaz, ami óriási feladat volt,így a matematikusok számítógépes technikákra támaszkodtak, hogy olyan algoritmusokat írjanak, amelyek képesek a számukra. Az algoritmusok Kempe módosított változatait használtáka láncok eredeti elképzelése más technikákkal együtt, hogy csökkentsék a minimális készlet tagjainak számát.
Miután együttműködik János Koch a probléma ofreducibility, 1976-ban a University of Illinois, Kenneth Appeland Wolfgang Haken végül csökkentette a vizsgálati probléma, hogy anunavoidable szett 1,936 konfigurációk, valamint egy teljes solutionto a Négy Szín Találgatás volt elérni. Ezt a problémát a térképek egyesével történő redukálhatóságának ellenőrzésével kétszer ellenőrizték különböző programokkal és különböző számítógépekkel. Bizonyítékaik azt mutatták, hogy legalább egy térkép, amelyen a lehető legkisebb számú régió található, öt színre van szükség, nem létezhet.
az első bizonyíték óta hatékonyabb algoritmusokat találtak a 4-színező térképekhez, és 1994-re az elkerülhetetlen konfigurációk száma 633-ra csökkent.
A számítógépen végzett “bizonyíték” megfelelő bizonyíték?
mivel a bizonyítás számítógép segítségével történt, azonnali felháborodás történt. Sok matematikus és filozófus azt állítottahogy a bizonyíték nem volt legitim. Néhányan azt mondták, hogy az igazolások shouldonly lehet bebizonyította,’ az emberek, nem gépek, míg mások, a morepractical elme megkérdőjelezte a megbízhatóság, mind a algorithmsand a képessége, hogy a gépek végrehajtani hiba nélkül.A matematikusok által írt bizonyítékok közül azonban sok volthibásnak bizonyult, így a megbízhatósággal kapcsolatos érv üresnek tűnik.Bármi legyen is a vélemény, a helyzet komoly voltvitája a bizonyíték jellegéről, amely még mindig folytatódikma.
pedagógiai megjegyzésekhez:
használja a cikk tetején található megjegyzések fület, vagy kattintson ide .
Megjegyzések
- ennek részleteiről és az ebben található egyéb eljárásokról Robin Wilson négy szín című könyvében olvashatunk .
- a Csomókat lehet balkezes vagy jobbkezes, ma pedig ott areimportant alkalmazások ez a szálláshely a kémia, gyógyszertár,biológia, fizika. (Lásd: Pedagógiai Megjegyzések)
- William Rowan Hamilton (1805-1865) után nevezték el. Egy hamiltoni út egy grafikon látogatásábanminden csúcs pontosan egyszer. A Hamiltoni ciklus (vagy kör) apath, amely minden csúcsot pontosan egyszer látogat meg, és visszatér a csúcshoz.(Lásd: Pedagógiai Megjegyzések)
- Lakatos Imre könyve, Bizonyítások és cáfolatok Cauchy eljárásának kritikája (6-12. oldal), és Euler tételének története.
- a kettősség gondolata a 16.és 17. században merült fel a projektív geometria fejlődésével. Az olyan matematikusok, mint Pascal ésdesargues úgy találták, hogy új tételeket lehet találni a determs ‘point’ és ‘line’ cseréjével bizonyos geometriai alakzatok leírásában. Példa erre a rendszeres polyhedra, ahol aaz egyik csúcsai megfelelnek a másik arcának. Tehát a tetraéder dualofja egy másik tetraéder,a kocka kettős pedig egy oktaéder. A kettős kettős kettős az eredetipóliéder.
a legjobb népszerű, könnyen olvasható könyv a négy színről:
Wilson, R. (2003)
négy szín elegendő.
London. Pingvin Könyvek.
részletesebb és technikatörténeti szempontból a standardreference könyv a következő:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Gráfelmélet,1736-1936
Oxford. Oxford University Press.
Ez naprakész, újabb alapokkal ésfilozófiával.
Fritsch, R and Fritsch, G (2000)
The Four Color Theorem: History,Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
alig van általános történelemkönyv a témában, de a Katz “számítógépek és alkalmazások” című utolsó fejezete a Gráfelméletről szól, és a négy Színtételről is szó esik.
Polya G. Hogyan kell SolveIt.
Ez a klasszikus könyv a problémamegoldásról. A könyv számos kiadása volt, mivel először az 1950-es években jelent meg, ésmég mindig könnyen elérhető. Érdekes módon a legutóbbi kiadásokat “a matematikai módszer új aspektusa” alcímmel adták meg.
Lakatos, I. (1976) bizonyít andRefutations: the Logic of Mathematical Discovery.
Cambridge. C. U. P.
Ez egy másik fontos könyv, amely az 1970-es évek kutatásaihoz vezetett. Úgy kezdődik, mint egy tanár és egy diákcsoport közötti vita az Euler képletének bizonyításáról, és a tizenkilencedik században a matematikusok és a tudósok által ténylegesen megvitatott eszmék,kifogások és lehetőségek között mozog. A tanításról és a tanulásról, valamint a matematikai módszerekről és a bizonyításról szóló legfontosabb kérdéseket emeli ki.
kapcsolódó hivatkozások
egy ideje volt egy kis könyvem a Karakterláncos játékokról. Amikor az iskolában voltam, Cat ‘ S Cradle-nek hívták, és a mi korunkban játszottuk.
a közelmúltban egy francia folyóirat kiadott egy tanulmányt a karakterláncok “algebra” – járól! Ha az Amazonra megy, megtalálja Ann Swain és Michael Taylor Finger Strings: A Book of Cats Cradles című könyvét és a Floris books által 2008 szeptemberében kiadott számadatokat. Van néhány 80 számok leírt színes diagrams.It a spirál kötött, így nyitva marad, amíg követi az utasításokat. Ez is jön egy pár string hurkok!
a csomós szakértők számára a Csomóshook of Knots egy klasszikus, bárki számára, aki érdeklődik a különböző típusú csomók és azok felhasználása iránt. Az Amazon rendelkezikkülönböző kiadások különböző áron érhetők el.
Webhivatkozások
a sok emberre és témára mutató általános áttekintéshez és linkekhez a theMacTutor weboldala
, és természetesen a MacTutor életrajzok az érintettekről a MacTutor Biographies indexben találhatók.
a négy Színtétel és három bizonyíték. A matematikus számára a következő weboldal érdekes új megközelítéssel rendelkezik, amely a probléma megoldására egy új algoritmus felépítésének problémáját oldja meg, valamint a számítógépre való támaszkodás csökkentését szolgálja.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
a Gráfelmélethez A Wikipédia jó áttekintést ad, és az igazán technikai dolgokat is megismerheti. Megmutatja a modern típusokata matematika ezen területének alkalmazása. Ha megy a GraphColouring, majd kattintson a négy szín tétel, akkor talál egy csomó további információt.
a Csomóelmélet érdekes és nem túl technikai története – Hogyan tér vissza Kelvin fizikája az Atomelmélethez.
A matematika tanárainak Szövetsége kelta Knotdesign plakátokkal rendelkezik. Látogasson el a honlapjukra, keresse meg az ábécétaz erőforrások listája.
Tudjon meg mindent a csomókról a csomó Atlaszán! Ha nem vagy anexpert – csak élvezd a “inhe spirit of wiki”adatbázis változatosságát és összetettségét
több művészi és színes-de nem kevésbé matematikai a theKnot telek oldal.
azok számára, akik az eredeti dolgok egy részét és a historicaldetailt szeretnék, a Csomóelmélet története a következő címen található: