2.5: Darcy Törvény – Flow a Porózus Közeg
Darcy törvény létfontosságú ahhoz, hogy megértsük számos ága geológia, különösen hidrogeológia. Mielőtt megnézzük a törvényt, és azt, hogy mit tud mondani nekünk, nézzük meg, hogyan alakult ki. Darcy törvényét Henry Darcy-ról nevezték el, egy 19. századi francia mérnök, aki földalatti nyomás alatt álló csőrendszert fejlesztett ki Dijon városának vízellátására. A rendszer, amely a híres Dijon szökőkutaknak is vizet biztosított, forradalmasította a városi víz-és szennyvízrendszert. A rendszer nem igényelt szivattyúkat, és pusztán a gravitáció vezérelte. Az új rendszer kifejlesztése során Darcy számos kísérletet végzett, ahol kizárólag gravitációval próbálta mozgatni a vizet.
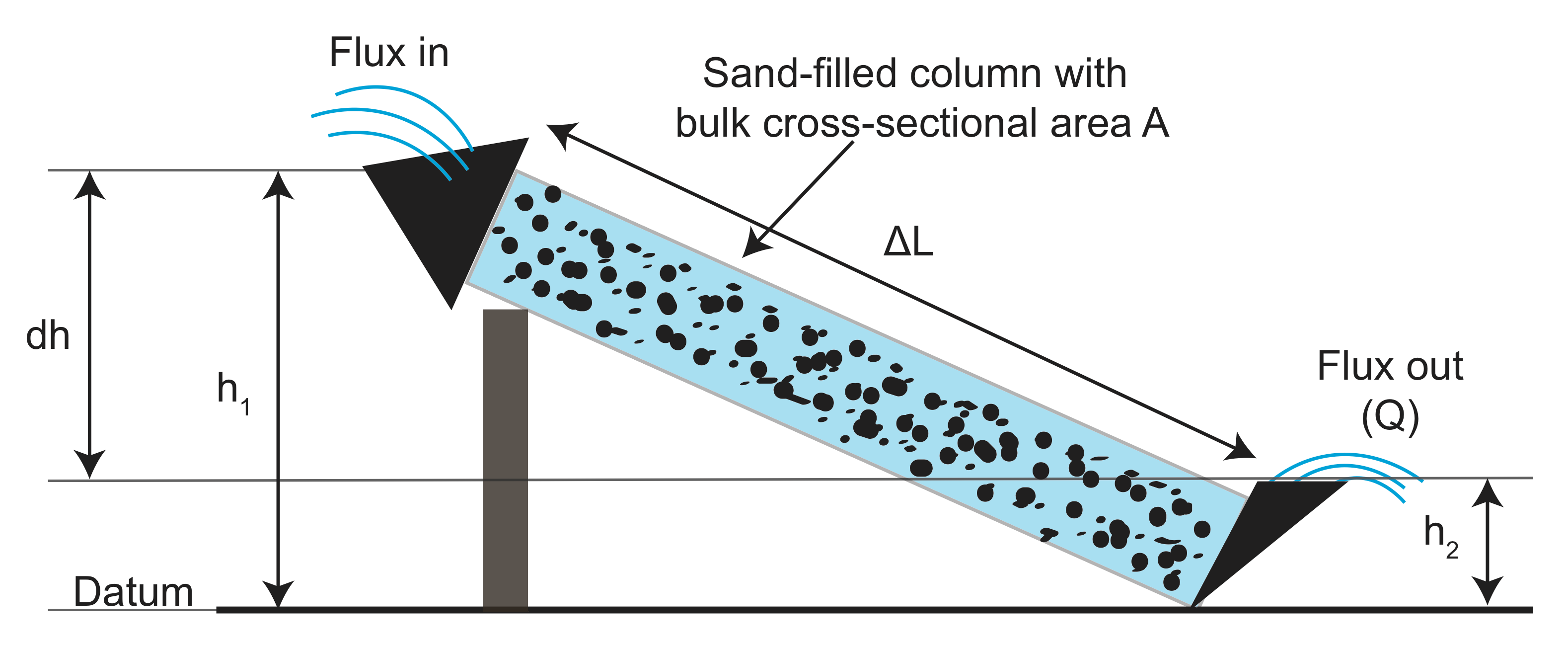
a kísérletek, adatokat gyűjtött a hossza a szűkítő (\(L\)), a keresztmetszeti területe a szűkítő (\(A\)), a magasság különbség (\(h_1 – h_2\)), a fluxus, a víz jön ki \(Q\) mindkét nélkül szemcsés (szűrés) anyag a szűkítő. Ezután ábrázolta a terület által normalizált fluxusmérést a magasságkülönbség arányával szemben a flume hosszával (\(\frac{h_1-h_2}{l}\)). Azt találta, hogy lineáris összefüggés van, és a lejtés függ a flume-ban használt szemcsés anyagtól:
\
, amely származékként átírható,
\
ahol \(K\) a hidraulikus vezetőképesség és \(\frac{DH}{DX}\) a hidraulikus gradiens. \(Q\), A teljes kisülési sebesség, \(\frac{m^3}{s}\) egységekkel rendelkezik, a víz mennyisége egy időben. A negatív jel annak a ténynek köszönhető, hogy a folyadék leáramlik (negatív) a hidraulikus gradiens magasabb értékekről alacsonyabb értékekre.
a hidraulikus vezetőképesség olyan fizikai paraméter, amely megmagyarázza, hogy a folyadék milyen könnyen mozoghat az anyag pórusterén. Darcy eredeti kísérleteiben különböző szemcseméretű homokot használt, azonban a hidraulikus vezetőképesség meghatározható szilárd kőzetekre is, mivel a legtöbb kőzetnek van némi pórusterülete.
Darcy eredeti kísérleteit követően további munkát végeztek a folyadék és a kőzet fizikai tulajdonságainak megértése érdekében, amelyek meghatározzák a hatékony hidraulikus vezetőképességet. Ezekből a kísérletekből kiderült, hogy
\
ahol \ (k\) a porózus közeg belső permeabilitása (a szilárd anyag), \(\eta\) a folyadék dinamikus viszkozitása, és \(\gamma = \Rho g\) a folyadék fajsúlya, amely a folyadék sűrűségétől, \(\rho\) és a gravitációtól függ, \(g\).
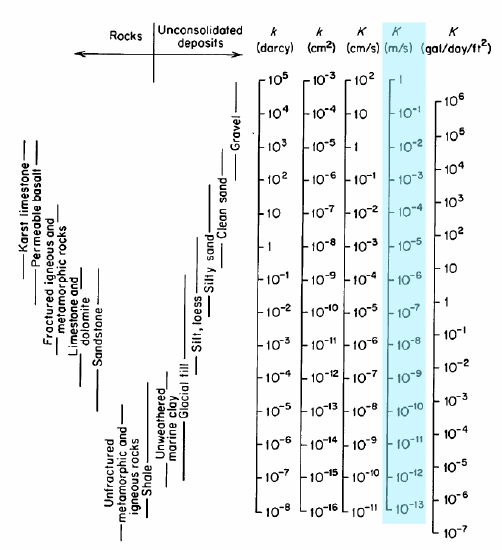
az ábrán a kiemelt oszlop K, a hidraulikus vezetőképesség \(\frac{m}{s}\); ezek azok az egységek, amelyeket használni fogunk. A hidraulikus vezetőképességet néha a belső permeabilitás szempontjából is jelentik, \(k\), darcys vagy cm2 egységekkel. A hidraulikus vezetőképesség teljes értéktartománya 1-10-13 \(\frac{m}{s}\). Az olyan kísérleteket, mint a Darcy-K, valódi anyagokban mérik a K-t.
a kisülési sebesség \(Q\) egy térfogatáram (\(m^3/S\)), de általában a folyadék áramlására gondolunk sebesség vagy sebesség szempontjából. A kisülési kérdések átrendezhetők úgy, hogy a területet elosztják a
\]
vagy a belső permeabilitás és nyomásgradiens szempontjából,
\
ahol\(\eta\) a folyadék viszkozitása (lásd alább a második egyenlet levezetését).
fontos megjegyezni, hogy a Darcy fluxus nem egyenlő a folyadék sebességével, annak ellenére, hogy sebességegységekben van. A folyadék sebessége az átlagos lineáris sebességen (\(v_a\) keresztül található meg, amely az összes lehetséges folyadékút sebességének átlaga a porózus közegen keresztül: de ennek az értéknek a megtalálása ezen osztály körén kívül esik. Ehelyett megjegyezzük, hogy a folyadék sebessége
\
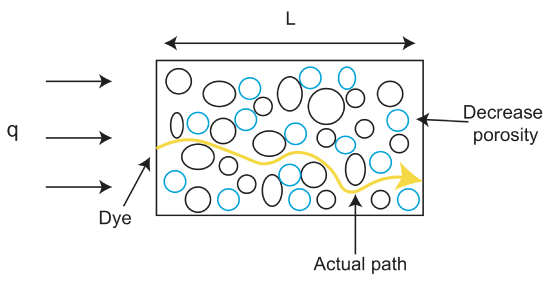
ahol \(\varphi\) a porozitás, v pedig a folyadék sebessége. A porozitás, \(\varphi\) az ürességtér térfogatának a \(\varphi=\frac{v_{void}}{v_{tot}}\) anyag teljes térfogatához viszonyított arányaként kerül kiszámításra, és általában 0 és 1 közötti frakcióként vagy százalékként fejeződik ki. Vegye figyelembe, hogy ha \(\varphi\leq\)1, akkor a folyadék sebessége nagyobb, mint a darcy fluxus.
egy másik kifejezés, amely akkor merül fel, amikor a sziklákon és a nem konszolidált anyagokon keresztül folyik, a permeabilitás. Míg a porozitás a kőzetben lévő pórusok (üregek) tényleges töredéke, ezek az üregek különböző formájúak és eltérő összekapcsolódásúak lehetnek, ami befolyásolja, hogy a folyadék milyen könnyen mozoghat a pórustérben. A permeabilitás annak a mértéknek a mértéke, amellyel a folyadékok és gázok könnyedén áthaladhatnak egy sziklán. Minél konszolidáltabb az anyag, annál alacsonyabb a permeabilitása. Így a” laza ” anyagok, mint a kavics, nagy áteresztőképességgel rendelkeznek. Egyes kőzetek anizotróp permeabilitással is rendelkezhetnek, ami azt jelenti, hogy a folyadékok könnyen áramlhatnak az egyik irányba, de nem a másikba. Az anizotróp permeabilitású szikla példája egy pala. A folyadékok könnyen mozoghatnak a pala rétegében, de nem mozoghatnak a rétegeken.
folyadéksebesség
tegyünk egy alapvető példát.
azt kapjuk, hogy \(q=2\frac{m}{min}\) és \(\varphi\) 25%, és meg akarjuk találni a folyadék sebességét.
először 25% – ot konvertálunk 0, 25-re.
ezután \(v = \ frac{2}{0.25} \ frac{m}{min}\)
és
\(v=8 \ frac{m}{min}\) a folyadék sebessége.
hidraulikus Fej
visszatérve Darcy kísérleteihez, mi a fizikai folyamat valójában a folyadék áramlását a flume-on keresztül vezet?
a \(\frac{dh}{dx}\) kifejezést hidraulikus fejnek nevezik, amely a folyadék nyomása a folyadék súlyának köszönhetően bizonyos referenciahelyhez viszonyítva: nyomásgradiens. A \ (\frac{DH}{dx} \) azonban nem rendelkezik egységnyi nyomású egységekkel, ezért miért hívják hidraulikus fejnek?
nézzük meg, mi a nyomás a flume-ban Darcy kísérleteiben. A kísérletek elvégzése érdekében Darcy-nak volt egy víztartálya a flume felső végén, amely állandó vízszintet biztosított a flume tetején, ami megegyezik a flume magasságával, \(h_1\). Hasonlóképpen, az alján egy tartály volt, amelynek állandó vízszintje megegyezik a \(h_2\) értékkel. Ezért a víz súlya miatt az egyes tartályokban a folyadéknyomást \(P = \rho g h\) adja. A nyomásgradiens a cső felső és alsó része között ekkor
\
vagy
\
>
>
&
= \ frac{k} {\rho g} \ frac{dp}{DX} \ end {align}}}. \ ]
emlékezzünk, felülről, hogy a hidraulikus vezetőképesség a belső permeabilitás szempontjából írható, mint \(k = k \ FRAC{\gamma} {\eta}\), amely egyenértékű \(k\frac{\rho g}{\eta}\) vagy átrendezve, \(\frac{k}{\rho g} = \ FRAC{k} {\eta} \). Ezért helyettesítheti, hogy a két azonos kifejezések a Darcy Törvény, egy korlátozott a gradiens magasság,
\
a második szempontjából a gradiens nyomás,
\
Így a \(\frac{dh}{dx}\) az úgynevezett hidraulikus fejét, mert a fizikai eredetű kifejezés a Darcy Törvény a nyomás gradiens a folyadék, ami vezérli az áramlás.
víz, amely egy víztartó réteget hagy
most tegyünk egy példát a víztartó rétegbe belépő víz folyadéksebességének kiszámítására. A víztartó magasság alatti vázlat a patak mellett a völgy melletti dombon található topográfiát követi. A víz nagy nyomású (fejmagasságú) folyóból folyik a völgy felé, és a patak vizét elhagyja. Felhasználhatjuk Darcy törvényét a vízáramlás sebességének becslésére, amely a víztartó réteget képezi.
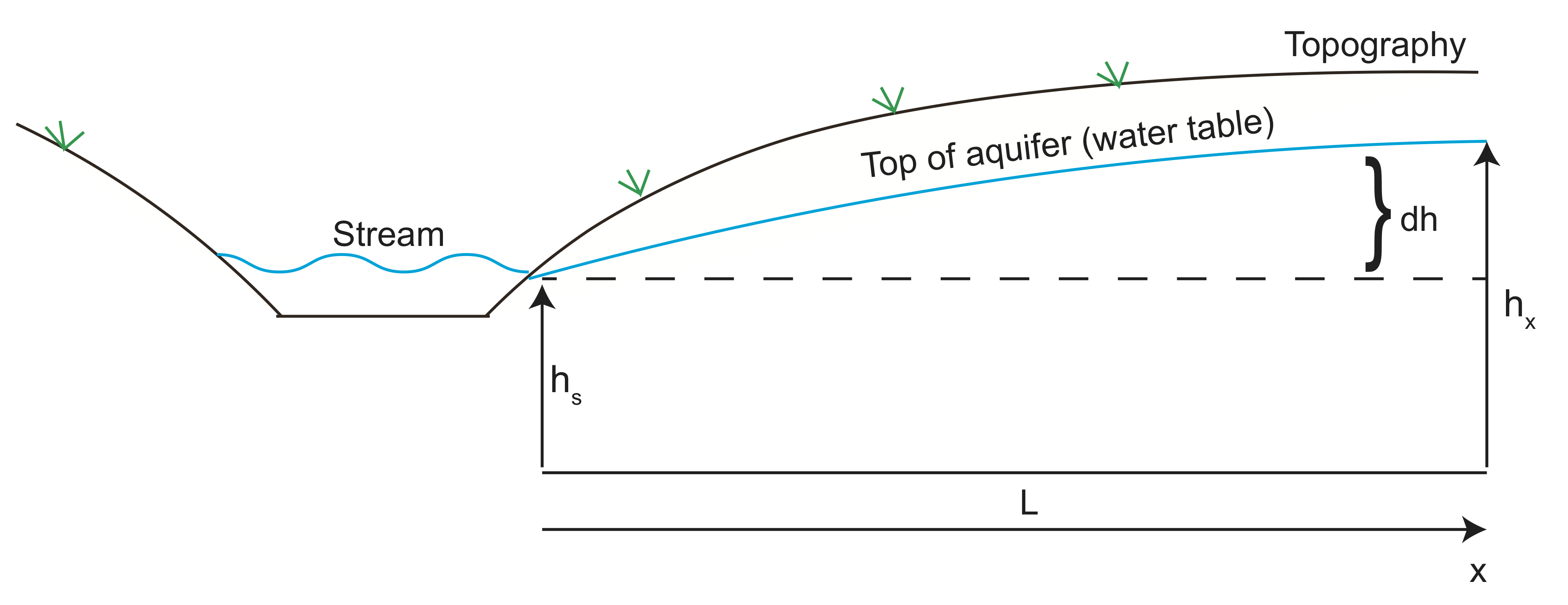
segítségével Geofizikai képalkotás, a magassága a vízadó található, hogy 10 m (\(dh\))) felett a patak magassága körülbelül 100 méter (\(L\)) távol. Tegyük fel, hogy a hidraulikus vezetőképesség \( K=10^{-6}\) m/s, a porozitás pedig \ (\varphi=30\)%.
A darcy fluxus
\
\
\
A folyadék sebessége
\
\
\
\

Laminar versus turbulens Flow
az egyik implicit feltételezés Darcy törvényében az, hogy az áramlás laminar. A lamináris áramlást úgy jellemzik, hogy vékony rétegekből vagy folyékony laminákból áll, amelyek egymással párhuzamosan mozognak. Ezzel szemben a turbulens áramlást örvények, örvények és örvények jellemzik, amelyekben a szomszédos folyadékrétegek eltérnek egymástól, és különböző útvonalakat vezetnek le.
az egyik módja annak, hogy számszerűsítsük, hogy egy folyadék lamináris vagy turbulens, A Reynold számának kiszámításával az áramláshoz, amelyet
\
A Reynold száma az áramlás momentumegyenlegében szereplő két kifejezés figyelembevételével található meg. Az első kifejezés az egységnyi térfogatra jutó inerciális erő, amely az áramlást hajtja, \(\rho u \ frac{du}{dx}\). A második kifejezés az egységnyi térfogatra jutó viszkózus erő, amely ellenáll az áramlásnak, \(\eta \ frac{d^2U}{dx^2}\). Ennek a két kifejezésnek egyensúlyban kell lennie, így egyenlőnek állíthatjuk be őket,
\
ezután átírjuk a kifejezéseket, egyszerűsített módon, hogy csak a változók megfelelő méreteit rögzítsük. Ehhez átmegyünk az úgynevezett dimenziós elemzésen,amelyben az egyes változókat referenciaértékekkel helyettesítjük, a változó nem dimenziós formáját.
például a \(x\) kifejezést átírják, mint csak \(L x’\), ahol \(L\) a referenciahossz (a folyadékmélység) és \(x’\) a nem dimenziós távolság. Hasonlóképpen hagyjuk \(u = u_o u’\). Helyettesítő ezek az egyenlethez jutunk
\
a Következő kombináljuk az állandó értékek elől
\
Megjegyezzük, hogy a kombináció a változók előtt a Reynolds szám
\
ahol a változók \(u_o\) áramlási sebesség, L folyadék mélység, valamint a változók korábban láttuk, \(\rho\) a folyadék sűrűsége, valamint a \(\eta\) folyadék viszkozitását. Az elemzés során azt találjuk, hogy minden olyan áramlás, amelyet e két kifejezés egyensúlya jellemez, összehasonlítható azzal, hogy egyszerűen megismerjük a Reynolds számának értékét. Például, ha az egyik áramlásnak viszkozitása van, amely egy másik áramlásban a viszkozitás 10-szerese, akkor a két áramlás ugyanúgy viselkedik, ha a sűrűséget (vagy sebességet vagy hosszúságot) szintén 10-szeresére növelik a nagyobb viszkozitású eset esetén; vagyis a két áramlás Reynolds száma megegyezik.
ahhoz, hogy Darcy flow legyen, A Reynold számának kevesebbnek kell lennie, mint 1-10 (laminar). Mert \(Re>1-10\) az áramlás nem szigorúan lamináris, de még nem turbulens (nem lineáris, nem laminár). A turbulens áramláshoz A Reynold számának nagyobbnak kell lennie, mint 2000 körül.
annak megértése, hogy a számlálóban és a nevezőben lévő állandók ellentétes módon befolyásolják az áramlás jellemzőit, szintén segít abban, hogy gondolkodjunk arról, hogy a különböző folyadékok hogyan viselkednek hasonló külső körülmények között. Például egy sűrűbb folyadék, amelynek gyors sebessége is van, nagyobb lesz, és turbulens viselkedést mutat. Ezzel szemben egy olyan folyadék, mint a nagy viszkozitású jég, amely nagyon lassan mozog, alacsony Re-vel rendelkezik, és valószínűleg lamináris áramlással rendelkezik. A jég nagy viszkozitása stabilizálja az áramlást. Egy másik példa, fontolja meg, hogy két folyadék ugyanolyan sebességgel mozoghat, másképp viselkedik, ha a Reynold számában lévő többi érték\(\frac {\rho l} {\mu}\) különbözik. Ezért az áramlási típus nem csak az áramlási sebességtől függ, hanem a Reynold-szám változóinak kombinációjától is.
A Darcy áramlásának alkalmazása
a Darcy törvénye a fő egyenlet, amely szabályozza a víztartó rétegek és kutak áramlását. Enélkül nem tudnánk kutakat fúrni, vagy megérteni a vízmozgást a víztartó rétegekben, különösen a Kaliforniai Központi völgyben, ahol mindkét ötlet kulcsfontosságú mind a mezőgazdasági termelékenység, mind a talajvíz süllyedése szempontjából.
