La régression vers la moyenne est un phénomène statistique courant qui peut nous induire en erreur lorsque nous observons le monde. Apprendre à reconnaître quand une régression vers la moyenne est en jeu peut nous aider à éviter de mal interpréter les données et de voir des modèles qui n’existent pas.

***

Il est important de minimiser les cas de mauvais jugement et d’aborder les points faibles de notre raisonnement. Apprendre la régression vers la moyenne peut nous aider.

Le psychologue lauréat du prix Nobel Daniel Kahneman a écrit un livre sur les biais qui brouillent notre raisonnement et déforment notre perception de la réalité. Il s’avère qu’il y a tout un ensemble d’erreurs logiques que nous commettons parce que notre intuition et notre cerveau ne traitent pas bien des statistiques simples. L’une des erreurs qu’il examine en pensant Vite et lentement est la régression infâme vers la moyenne.

La notion de régression vers la moyenne a été élaborée pour la première fois par Sir Francis Galton. La règle veut que, dans toute série avec des phénomènes complexes qui dépendent de nombreuses variables, où le hasard est impliqué, les résultats extrêmes ont tendance à être suivis de résultats plus modérés.

Dans Chercher la sagesse, Peter Bevelin donne l’exemple de John, qui était insatisfait de la performance des nouveaux employés, alors il les a mis dans un programme d’amélioration des compétences où il a mesuré les compétences des employés:

Leurs scores sont maintenant plus élevés qu’ils ne l’étaient au premier test. Conclusion de John: « Le programme d’amélioration des compétences a entraîné l’amélioration des compétences. » Ce n’est pas nécessairement vrai. Leurs scores plus élevés pourraient être le résultat d’une régression vers la moyenne. Étant donné que ces personnes ont été mesurées comme étant à l’extrémité inférieure de l’échelle de compétences, elles auraient montré une amélioration même si elles n’avaient pas suivi le programme d’amélioration des compétences. Et il pourrait y avoir de nombreuses raisons à leur performance antérieure — stress, fatigue, maladie, distraction, etc. Leur véritable capacité n’a peut-être pas changé.

Nos performances varient toujours autour d’une performance réelle moyenne. Les performances extrêmes ont tendance à devenir moins extrêmes la prochaine fois. Pourquoi? Les mesures de test ne peuvent jamais être exactes. Toutes les mesures sont composées d’une partie vraie et d’une partie d’erreur aléatoire. Lorsque les mesures sont extrêmes, elles sont susceptibles d’être en partie causées par le hasard. Le hasard est susceptible de contribuer moins à la deuxième fois que nous mesurons la performance.

Si nous passons d’une façon de faire quelque chose à une autre simplement parce que nous échouons, il est très probable que nous fassions mieux la prochaine fois, même si la nouvelle façon de faire quelque chose est égale ou pire.

C’est l’une des raisons pour lesquelles il est dangereux d’extrapoler à partir de petites tailles d’échantillon, car les données peuvent ne pas être représentatives de la distribution. C’est aussi la raison pour laquelle James March soutient que plus quelqu’un reste longtemps dans son travail, « moins la différence probable entre le rendement observé et la capacité réelle est grande. »Tout peut arriver à court terme, en particulier dans tout effort qui implique une combinaison d’habileté et de chance. (Le rapport entre la compétence et la chance a également un impact sur la régression vers la moyenne.)

Régression vers la moyenne

Les effets de la régression vers la moyenne peuvent fréquemment être observés dans le sport, où l’effet provoque de nombreuses spéculations injustifiées.

Dans Thinking Fast and Slow, Kahneman se souvient avoir regardé le saut à ski masculin, une discipline où le score final est une combinaison de deux sauts distincts. Conscient de la régression vers la moyenne, Kahneman a été surpris d’entendre les prédictions du commentateur sur le deuxième saut. Il écrit:

La Norvège a fait un bon premier saut; il sera tendu, espérant protéger son avance et fera probablement pire” ou « La Suède a fait un mauvais premier saut et maintenant il sait qu’il n’a rien à perdre et sera détendu, ce qui devrait l’aider à faire mieux.

Kahneman souligne que le commentateur avait remarqué la régression vers la moyenne et avait proposé une histoire pour laquelle il n’y avait aucune preuve causale (voir erreur narrative). Cela ne veut pas dire que son histoire ne pouvait pas être vraie. Peut-être que si nous mesurions les fréquences cardiaques avant chaque saut, nous verrions qu’elles sont plus détendues si le premier saut était mauvais. Cependant, ce n’est pas le problème. Le fait est que la régression à la moyenne se produit lorsque la chance joue un rôle, comme elle l’a fait dans le résultat du premier saut.

La leçon du sport s’applique à toute activité où le hasard joue un rôle. Nous attachons souvent des explications de notre influence sur un processus particulier au progrès ou à l’absence de celui-ci.

En réalité, la science de la performance est complexe, dépendante de la situation et souvent, une grande partie de ce que nous pensons être sous notre contrôle est vraiment aléatoire.

Dans le cas des sauts à ski, un vent fort contre le sauteur conduira même le meilleur athlète à des résultats médiocres. De même, un vent fort et des conditions de ski favorables à un sauteur médiocre peuvent entraîner une baisse considérable, mais temporaire de ses résultats. Ces effets, cependant, disparaîtront une fois que les conditions changeront et que les résultats reviendront à la normale.

Cela peut avoir de graves implications pour le coaching et le suivi des performances. Les règles de régression suggèrent que lors de l’évaluation du rendement ou de l’embauche, nous devons nous fier aux antécédents plus qu’aux résultats de situations spécifiques. Sinon, nous sommes enclins à être déçus.

Lorsque Kahneman donnait une conférence à l’Armée de l’air israélienne sur la psychologie de l’entraînement efficace, l’un des officiers a partagé son expérience selon laquelle l’éloge de ses subordonnés conduisait à de moins bonnes performances, tandis que la réprimande conduisait à une amélioration des efforts ultérieurs. En conséquence, il était devenu généreux avec les commentaires négatifs et était devenu plutôt prudent de donner trop d’éloges.

Kahneman a immédiatement remarqué qu’il s’agissait d’une régression vers la moyenne au travail. Il a illustré l’idée fausse par un exercice simple que vous voudrez peut-être essayer vous-même. Il a dessiné un cercle sur un tableau noir, puis a demandé aux officiers un à un de jeter un morceau de craie au centre du cercle, le dos tourné vers le tableau noir. Il a ensuite répété l’expérience et a enregistré la performance de chaque officier lors du premier et du deuxième essai.

Naturellement, ceux qui ont fait incroyablement bien au premier essai avaient tendance à faire pire au deuxième essai et vice versa. L’erreur est immédiatement devenue claire: le changement de performance se produit naturellement. Encore une fois, cela ne veut pas dire que la rétroaction n’a pas du tout d’importance – peut-être que oui, mais l’agent n’avait aucune preuve pour conclure que c’était le cas.

La Corrélation imparfaite et le hasard

À ce stade, vous vous demandez peut-être pourquoi la régression vers la moyenne se produit et comment nous pouvons nous assurer que nous en sommes conscients lorsqu’elle se produit.

Pour comprendre la régression vers la moyenne, il faut d’abord comprendre la corrélation.

Le coefficient de corrélation entre deux mesures qui varie entre -1 et 1, est une mesure du poids relatif des facteurs qu’elles partagent. Par exemple, deux phénomènes avec peu de facteurs partagés, comme la consommation d’eau embouteillée par rapport au taux de suicide, devraient avoir un coefficient de corrélation proche de 0. C’est-à-dire que si nous examinions tous les pays du monde et que nous indiquions les taux de suicide d’une année spécifique par rapport à la consommation d’eau en bouteille par habitant, le complot ne montrerait aucune tendance.

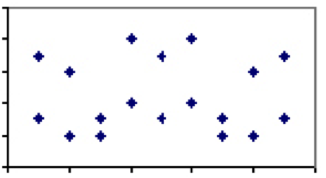
Au contraire, il existe des mesures qui dépendent uniquement du même facteur. La température en est un bon exemple. Le seul facteur déterminant la température – la vitesse des molécules — est partagé par toutes les échelles, donc chaque degré en Celsius aura exactement une valeur correspondante en Fahrenheit. Par conséquent, la température en Celsius et Fahrenheit aura un coefficient de corrélation de 1 et le tracé sera une ligne droite.

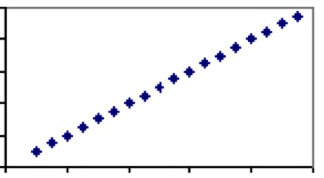
Il y a peu ou pas de phénomènes en sciences humaines qui ont un coefficient de corrélation de 1. Il y en a cependant beaucoup où l’association est faible à modérée et il y a un certain pouvoir explicatif entre les deux phénomènes. Considérez la corrélation entre la taille et le poids, qui se situerait quelque part entre 0 et 1. Alors que pratiquement tous les enfants de trois ans seront plus légers et plus courts que tous les hommes adultes, tous les hommes adultes ou les enfants de trois ans de même taille ne pèseront pas le même poids.

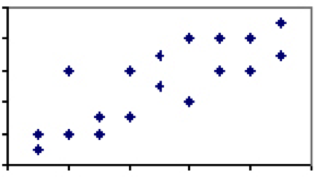
Cette variation et le degré de corrélation inférieur correspondant impliquent que, bien que la hauteur soit généralement un bon prédicteur, il existe clairement d’autres facteurs que la hauteur en jeu. Lorsque la corrélation de deux mesures est moins que parfaite, nous devons faire attention aux effets de la régression vers la moyenne.

Kahneman a observé une règle générale: Chaque fois que la corrélation entre deux scores est imparfaite, il y aura régression vers la moyenne.

Au premier abord, cela peut sembler déroutant et peu intuitif, mais le degré de régression vers la moyenne est directement lié au degré de corrélation des variables. Cet effet peut être illustré par un exemple simple.

Supposons que vous soyez à une fête et demandez-vous pourquoi les femmes très intelligentes ont tendance à épouser des hommes moins intelligents qu’elles ne le sont. La plupart des gens, même ceux qui ont une formation en statistiques, se lanceront rapidement avec une variété d’explications causales allant de l’évitement de la concurrence aux craintes de solitude auxquelles ces femmes sont confrontées. Un sujet d’une telle controverse est susceptible de susciter un grand débat.

Maintenant, et si nous demandions pourquoi la corrélation entre les scores d’intelligence des conjoints est moins que parfaite? Cette question n’est guère aussi intéressante et il y a peu à deviner – nous savons tous que cela est vrai. Le paradoxe réside dans le fait que les deux questions sont algébriquement équivalentes. Kahneman explique:

Si la corrélation entre l’intelligence des conjoints est moins que parfaite (et si les hommes et les femmes en moyenne ne diffèrent pas en intelligence), alors il est une fatalité mathématique que des femmes très intelligentes soient mariées à des maris qui sont en moyenne moins intelligents qu’elles (et vice versa, bien sûr). La régression observée vers la moyenne ne peut être plus intéressante ou plus explicable que la corrélation imparfaite.

En supposant que la corrélation est imparfaite, les chances de deux partenaires représentant les 1% supérieurs en termes de caractéristique sont beaucoup plus petites qu’un partenaire représentant les 1% supérieurs et l’autre – les 99% inférieurs.

La Cause, l’effet et le traitement

Nous devons nous méfier particulièrement de la régression vers le phénomène moyen lorsque nous essayons d’établir la causalité entre deux facteurs. Chaque fois que la corrélation est imparfaite, le meilleur semblera toujours s’aggraver et le pire semblera s’améliorer avec le temps, indépendamment de tout traitement supplémentaire. C’est quelque chose que les médias en général et parfois même les scientifiques formés ne parviennent pas à reconnaître.

Prenons l’exemple donné par Kahneman:

Les enfants déprimés traités avec une boisson énergisante s’améliorent considérablement sur une période de trois mois. J’ai inventé ce titre de journal, mais le fait qu’il rapporte est vrai: si vous traitiez un groupe d’enfants déprimés pendant un certain temps avec une boisson énergisante, ils montreraient une amélioration cliniquement significative. Il est également vrai que les enfants déprimés qui passent du temps debout sur la tête ou qui étreignent un chat pendant vingt minutes par jour montreront également une amélioration.

Chaque fois que vous rencontrez de tels titres, il est très tentant de conclure que les boissons énergisantes, debout sur la tête ou les chats enlacés sont tous des remèdes parfaitement viables pour la dépression. Ces cas, cependant, incarnent une fois de plus la régression vers la moyenne:

Les enfants déprimés sont un groupe extrême, ils sont plus déprimés que la plupart des autres enfants — et les groupes extrêmes régressent à la moyenne avec le temps. La corrélation entre les scores de dépression à des occasions successives de tests est moins que parfaite, il y aura donc régression vers la moyenne: les enfants déprimés s’amélioreront un peu avec le temps, même s’ils n’embrassent pas de chats et ne boivent pas de Taureau rouge.

Nous attribuons souvent à tort une politique ou un traitement spécifique comme cause d’un effet, alors que le changement dans les groupes extrêmes se serait produit de toute façon. Cela pose un problème fondamental: comment savoir si les effets sont réels ou simplement dus à la variabilité?

Heureusement, il existe un moyen de distinguer entre une amélioration réelle et une régression vers la moyenne. C’est l’introduction du soi-disant groupe témoin, qui devrait s’améliorer par la seule régression. Le but de la recherche est de déterminer si le groupe traité s’améliore plus que la régression ne peut l’expliquer.

Dans des situations de la vie réelle avec la performance d’individus ou d’équipes spécifiques, où la seule référence réelle est la performance passée et où aucun groupe témoin ne peut être introduit, les effets de la régression peuvent être difficiles, voire impossibles à démêler. Nous pouvons comparer la moyenne de l’industrie, les pairs du groupe de cohortes ou les taux d’amélioration historiques, mais aucune de ces mesures n’est parfaite.

***

Heureusement, la prise de conscience de la régression vers le phénomène moyen lui-même est déjà un premier pas vers une approche plus prudente pour comprendre la chance et la performance.

S’il y a quelque chose à apprendre de la régression vers la moyenne, c’est l’importance des antécédents plutôt que de s’appuyer sur des réussites ponctuelles. J’espère que la prochaine fois que vous tomberez sur une qualité extrême en partie régie par le hasard, vous vous rendrez compte que les effets sont susceptibles de régresser avec le temps et ajusteront vos attentes en conséquence.

Que lire ensuite

• Améliorez votre pensée avec 113 modèles mentaux expliqués.
• Lisez à propos de la pensée de deuxième niveau afin d’éviter les conséquences négatives.