Note de la rédaction

Le rapport de recherche étudiant suivant a été préparé pour la classe de mathématiques 255 du professeur Judit Kardos, tenue au College of New Jersey. Il s’agissait d’un cours d’introduction de 3 crédits à l’histoire des mathématiques. Ce rapport a été compté pour 30% de la note finale. C’est un exemple du genre de recherche historique que les étudiants peuvent faire en utilisant des sources secondaires.

La solution de Leonard Euler au problème du pont de Königsberg

Königsberg

Notre histoire commence au 18ème siècle, dans la pittoresque ville de Königsberg, en Prusse, sur les rives de la rivière Pregel. En 1254, les chevaliers teutoniques fondent la ville de Königsberg sous la direction du roi de Bohême Ottoker II après leur deuxième croisade contre les Prussiens. Au Moyen Âge, Königsberg est devenue une ville et un centre commercial très important grâce à son emplacement stratégiquement situé sur la rivière. Des œuvres d’art du XVIIIe siècle montrent Königsberg comme une ville prospère, où des flottes de navires remplissent le Pregel, et leur commerce offre un style de vie confortable aux marchands locaux et à leurs familles. L’économie saine a permis aux habitants de la ville de construire sept ponts sur la rivière, dont la plupart reliés à l’île de Kneiphof; leurs emplacements sont visibles sur la photo ci-jointe.

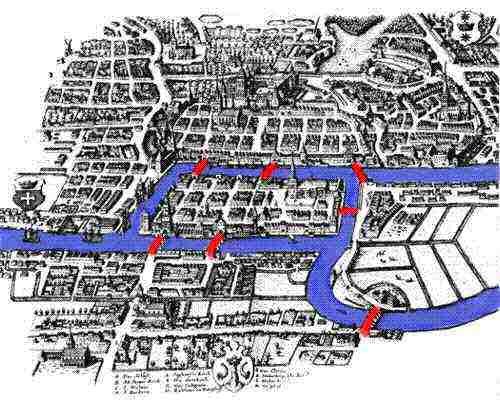
Comme la rivière coulait autour de Kneiphof, signifiant littéralement la cour du pub, et une autre île, elle divisait la ville en quatre régions distinctes. Les sept ponts s’appelaient Pont du Forgeron, Pont de Liaison, Pont Vert, Pont du Marchand, Pont en Bois, Pont Haut et Pont de Miel. Selon la tradition, les citoyens de Königsberg passaient le dimanche après-midi à se promener dans leur belle ville. En marchant, les habitants de la ville ont décidé de se créer un jeu, leur objectif étant de concevoir un moyen de se promener dans la ville, en ne traversant chacun des sept ponts qu’une seule fois. Même si aucun des citoyens de Königsberg ne pouvait inventer un itinéraire qui leur permettrait de traverser chacun des ponts une seule fois, ils ne pouvaient toujours pas prouver que c’était impossible. Heureusement pour eux, Königsberg n’était pas trop loin de Saint-Pétersbourg, la maison du célèbre mathématicien Leonard Euler.

Euler et le problème du Pont

Pourquoi Euler se préoccuperait-il d’un problème si indépendant du domaine des mathématiques? Pourquoi un si grand mathématicien passerait-il beaucoup de temps avec un problème trivial comme le problème du pont de Königsberg? Euler était évidemment un homme occupé, publiant plus de 500 livres et articles au cours de sa vie. En 1775 seulement, il a écrit en moyenne un article de mathématiques par semaine, et au cours de sa vie, il a écrit sur une variété de sujets en plus des mathématiques, y compris la mécanique, l’optique, l’astronomie, la navigation et l’hydrodynamique. Il n’est pas surprenant qu’Euler ait estimé que ce problème était trivial, déclarant dans une lettre de 1736 à Carl Leonhard Gottlieb Ehler, maire de Dantzig, qui lui demandait une solution au problème :

. . . Ainsi, vous voyez, très noble Monsieur, comment ce type de solution a peu de rapport avec les mathématiques, et je ne comprends pas pourquoi vous attendez d’un mathématicien qu’il la produise, plutôt que quiconque, car la solution est basée sur la seule raison, et sa découverte ne dépend d’aucun principe mathématique. Pour cette raison, je ne sais pas pourquoi même des questions qui ont si peu de rapport avec les mathématiques sont résolues plus rapidement par les mathématiciens que par d’autres.

Même si Euler a trouvé le problème trivial, il en était toujours intrigué. Dans une lettre écrite la même année à Giovanni Marinoni, un mathématicien et ingénieur italien, Euler a déclaré:

Cette question est si banale, mais me semblait digne d’attention en ce sens que la géométrie, ni l’algèbre, ni même l’art du comptage suffisaient à la résoudre.

Euler pensait que ce problème était lié à un sujet sur lequel Gottfried Wilhelm Leibniz avait déjà discuté et avait envie de travailler, quelque chose que Leibniz appelait geometria situs, ou géométrie de la position. Cette soi-disant géométrie de position est ce qu’on appelle maintenant la théorie des graphes, qu’Euler introduit et utilise pour résoudre ce fameux problème.

Preuve d’Euler

Le 26 août 1735, Euler présente un document contenant la solution au problème du pont de Konigsberg. Il aborde à la fois ce problème spécifique, ainsi qu’une solution générale avec un nombre quelconque de masses terrestres et un nombre quelconque de ponts. Cet article, intitulé « Solutio problematis ad geometriam situs pertinentis », a été publié plus tard en 1741. Le document d’Euler est divisé en vingt et un paragraphes numérotés, et dans ce qui suit, une version simplifiée des paragraphes d’Euler sera présentée.

Dans les deux premiers paragraphes de la preuve d’Euler, il introduit le problème du pont de Konigsberg. Au paragraphe 1, Euler déclare qu’il pense que ce problème concerne la géométrie, mais pas la géométrie bien connue de ses contemporains, qui implique des mesures et des calculs, mais plutôt un nouveau type de Géométrie, que Leibniz a appelé Géométrie de Position. Ensuite, au paragraphe 2, Euler explique à son auditoire comment fonctionne le problème de Konigsberg. Euler a fourni une esquisse du problème (voir la figure 1 d’Euler) et a appelé les sept ponts distincts: a, b, c, d, e, f et, g. Dans ce paragraphe, il énonce la question générale du problème: « Peut-on savoir s’il est possible ou non de traverser chaque pont exactement une fois? »

Figure d’Euler 1 de ‘Solutio problematis ad geometriam situs pertinentis,’Eneström 53

Après avoir énoncé la question générale qu’il essaie de résoudre, Euler commence à explorer différentes méthodes pour trouver une solution. Au paragraphe 3, Euler dit au lecteur que pour résoudre ce problème spécifique, il pourrait écrire tous les chemins possibles, mais cette technique prendrait beaucoup de temps et ne fonctionnerait pas pour des configurations plus grandes avec plus de ponts et de masses terrestres. En raison de ces problèmes, Euler a décidé de choisir une méthode différente pour résoudre ce problème.

Au paragraphe 4, il commence à simplifier le problème en inventant un système pratique pour représenter le franchissement d’un pont. Euler décide qu’au lieu d’utiliser les lettres minuscules pour représenter la traversée d’un pont, il écrirait les lettres majuscules représentant les masses terrestres. Par exemple, en faisant référence à sa figure 1, AB signifierait un voyage qui a commencé dans la masse terrestre A et s’est terminé en B. De plus, si après avoir voyagé de la masse terrestre A à B, quelqu’un décide de passer à la masse terrestre D, cela serait simplement noté, ABD. Au paragraphe 5, Euler poursuit sa discussion sur ce processus en expliquant que dans ABDC, bien qu’il y ait quatre lettres majuscules, seuls trois ponts ont été franchis. Euler explique que peu importe le nombre de ponts, il y aura une lettre de plus pour représenter la traversée nécessaire. Pour cette raison, l’ensemble du problème du pont de Königsberg nécessitait sept ponts à franchir, et donc huit lettres majuscules.

Au paragraphe 6, Euler continue d’expliquer les détails de sa méthode. Il dit au lecteur que s’il y a plus d’un pont qui peut être franchi en passant d’une masse terrestre à l’autre, peu importe le pont utilisé. Par exemple, même s’il existe deux ponts, a et b, qui peuvent emmener un voyageur de A à B, peu importe avec la notation d’Euler quel pont est pris. Dans ce paragraphe, Euler discute également du problème spécifique auquel il est confronté. Il explique, en utilisant sa figure originale, que le problème de Königsberg nécessite exactement huit lettres, où les paires de (A, B) et (A, C) doivent apparaître exactement deux fois l’une à côté de l’autre, quelle que soit la lettre qui apparaît en premier. De plus, les paires (A, D), (B, D) et (C, D) doivent se rencontrer exactement une fois pour qu’un chemin qui traverse chaque pont une fois et une seule fois existe.

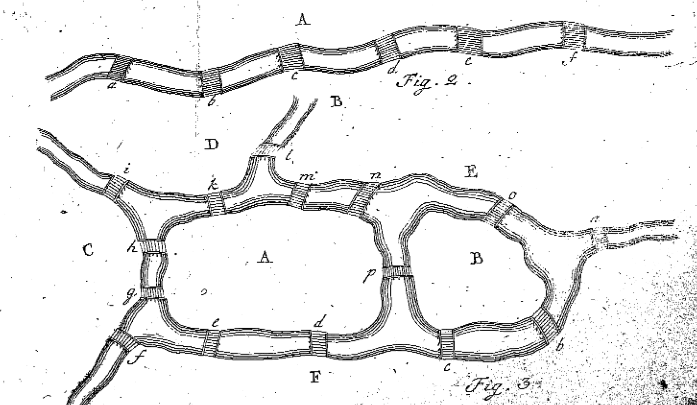
Figures d’Euler 2 et 3 de ‘Solutio problematis ad geometriam situs pertinentis,’Eneström 53

Au paragraphe 7, Euler informe le lecteur qu’il doit soit trouver une séquence de huit lettres qui satisfait le problème, soit prouver qu’il n’existe pas de telle séquence. Avant de le faire pour le problème du pont de Königsberg, il décide de trouver une règle pour découvrir s’il existe un chemin pour un problème plus général. Il le fait au paragraphe 8 en examinant des exemples beaucoup plus simples de masses terrestres et de ponts. Euler dessine la figure 2, et il commence à évaluer les situations dans lesquelles la région A est traversée. Euler déclare que si le pont a est parcouru une fois, A était soit l’endroit où le voyage a commencé ou s’est terminé, et n’a donc été utilisé qu’une seule fois. Si les ponts a, b et c sont tous parcourus une fois, A est utilisé exactement deux fois, qu’il s’agisse du lieu de départ ou de fin. De même, si cinq ponts mènent à A, la masse terrestre A se produirait exactement trois fois au cours du trajet. Euler déclare que, « En général, si le nombre de ponts est un nombre impair quelconque, et s’il est augmenté de un, alors le nombre d’occurrences de A est la moitié du résultat. »En d’autres termes, s’il y a un nombre impair de ponts reliant A à d’autres masses terrestres, ajoutez-en un au nombre de ponts et divisez-le par deux, pour savoir combien de fois au total A doit être utilisé dans le chemin, où chaque pont est utilisé une fois et une seule fois (i.e. Occurrences totales de A où A a un nombre impair de ponts = (nombre de ponts – 1) / 2).

En utilisant ce fait, Euler résout le problème du pont de Königsberg au paragraphe 9. Dans ce cas, puisqu’il y a cinq ponts qui mènent à A, cela doit se produire trois fois (voir sa figure 1, ci-dessus). De même, B, C et D doivent apparaître deux fois car ils ont tous trois ponts qui les mènent. Par conséquent, 3 (pour A) + 2 (pour B) + 2 (pour C) + 2 (pour D) = 9, mais Euler a déjà déclaré qu’il ne devait y avoir que huit occurrences pour les sept ponts. C’est une contradiction ! Par conséquent, il est impossible de parcourir les ponts de la ville de Königsberg une fois et une seule fois. La fin, ou est-ce? Alors que les habitants de Königsberg peuvent être satisfaits de cette solution, le grand mathématicien Leonhard Euler n’était pas satisfait. Euler poursuit en outre sa preuve pour traiter des situations plus générales.

Généralisation d’Euler

Au paragraphe 10, Euler poursuit sa discussion en notant que si la situation concerne toutes les masses terrestres avec un nombre impair de ponts, il est possible de dire si un trajet ne peut être effectué qu’une seule fois en utilisant chaque pont. Euler déclare que si la somme du nombre de fois que chaque lettre doit apparaître est une de plus que le nombre total de ponts, un voyage peut être effectué. Cependant, si le nombre d’occurrences est supérieur à un de plus que le nombre de ponts, un trajet ne peut pas être effectué, comme le problème du pont de Königsberg. En effet, la règle, que donne Euler pour un nombre impair de ponts, en utilisant sa figure 2, est vraie pour la situation générale, qu’il n’y ait qu’une seule autre masse terrestre ou plus d’une.

Aux paragraphes 11 et 12, Euler traite de la situation où une région a un nombre pair de ponts qui lui sont attachés. Cette situation n’apparaît pas dans le problème de Königsberg et a donc été ignorée jusqu’à présent. Dans la situation d’une masse terrestre X avec un nombre pair de ponts, deux cas peuvent se produire. Le premier cas est lorsque X est le point de départ du voyage. Dans ce cas, X apparaîtra deux fois, une fois comme point de départ et à nouveau comme point final. Dans l’autre cas, X n’est pas le point de départ. Si cela devait se produire, X n’apparaîtrait qu’une seule fois, car le voyage devrait entrer par un pont et sortir immédiatement par le seul autre disponible. De même, s’il y a quatre ponts attachés à X, le nombre d’occurrences de X dépend du point de départ ou non. Si le voyage commence en X, il doit apparaître trois fois, mais s’il ne commence pas en X, il n’apparaîtra que deux fois. Donc, en général, si X a un nombre pair de ponts attachés, alors si le trajet ne commence pas dans X, X apparaît la moitié du nombre de fois en tant que ponts (c’est-à-dire Occurrences de X où X est pair et non le point de départ = (nombre de ponts) /2). Si le trajet commence par X, alors X apparaît la moitié du nombre de fois en tant que ponts, plus un (c’est-à-dire les occurrences de X où X est pair et le point de départ = ((nombre de ponts) / 2) + 1).

Aux paragraphes 13 à 15, Euler explique comment déterminer si un chemin utilisant chaque pont une fois et une seule fois existe et présente son propre exemple pour montrer comment cela fonctionne. Euler explique d’abord sa méthode simple en six étapes pour résoudre toute situation générale avec des masses terrestres divisées par des rivières et reliées par des ponts. Euler désigne d’abord chaque masse terrestre par une lettre majuscule. Deuxièmement, il prend le nombre total de ponts, en ajoute un et l’écrit au-dessus du tableau qu’il s’apprête à faire. Ensuite, il prend les majuscules, les met dans une colonne et à côté d’eux écrit le nombre de ponts. Quatrièmement, il indique par des astérisques les masses terrestres qui ont un nombre pair de ponts. Ensuite, à côté de chaque nombre pair, il écrit ½ du nombre et à côté de chaque nombre impair, il place ½ le nombre plus un. Enfin, Euler ajoute les nombres écrits dans la colonne la plus à droite et si la somme est inférieure ou égale au nombre de ponts plus un, alors le trajet requis est possible. Il est important de noter cependant que si la somme est inférieure d’un au nombre de ponts plus un, le voyage doit commencer à partir de l’une des masses terrestres marquées d’un astérisque. Si la somme est égale au nombre de ponts plus un, le voyage doit commencer dans une région non marquée d’un astérisque.

Exemples

En utilisant le problème de Konigsberg comme premier exemple, Euler montre ce qui suit:

Nombre de ponts = 7, Nombre de ponts plus un = 8

Les temps des ponts de région Doivent Apparaître

A 5 3

B 3 2

C 3 2

D 3 2

Cependant, 3 + 2 + 2 + 2 = 9, ce qui fait plus de 8, donc le voyage est impossible.

Comme cet exemple est plutôt basique, Euler décide de concevoir sa propre situation avec deux îles, quatre rivières et quinze ponts. La situation créée par Euler peut être vue dans sa figure 3, ci-dessus. Euler tente maintenant de déterminer s’il existe un chemin qui permet à quelqu’un de franchir chaque pont une fois et une seule fois. Euler suit les mêmes étapes que ci-dessus, nommant les cinq régions différentes avec des lettres majuscules, et crée un tableau pour vérifier si c’est possible, comme suit:

Nombre de ponts = 15, Nombre de ponts plus un = 16

Les temps des ponts de région La région Doit apparaître

A *8 4

B * 4 2

C * 4 2

D 3 2

E 5 3

F*6 3

En plus, 4 + 2 + 2 + 2 + 3 + 3 = 16, ce qui équivaut au nombre de ponts, plus un, ce qui signifie que le voyage est, en fait, possible. Puisque la somme est égale au nombre de ponts plus un, le voyage doit commencer en D ou en E. Maintenant qu’Euler sait qu’il est possible de faire un voyage, il ne lui reste plus qu’à indiquer quel sera le chemin. Euler choisit le chemin EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, où il inclut les ponts croisés entre les lettres représentant les masses terrestres. Bien que cette information soit étrangère, comme le pont exact n’a pas d’importance pour savoir qu’un trajet est possible, elle est utile lors de la sélection d’un chemin. C’est un bon exemple qui montre la méthode qu’Euler utiliserait pour résoudre tout problème de cette nature.

Conclusions d’Euler

Dans les paragraphes suivants, Euler présente une autre façon de déterminer si un voyage peut être effectué compte tenu de n’importe quel ensemble de masses terrestres, de ponts et de rivières. Au paragraphe 16, Euler souligne que le total des numéros énumérés directement à droite des masses terrestres représente jusqu’à deux fois le nombre total de ponts. Ce fait devient plus tard connu sous le nom de lemme de poignée de main. Fondamentalement, le lemme de prise de contact indique que chaque pont est compté deux fois, une fois pour chaque masse terrestre à laquelle il est attaché. Au paragraphe 17, Euler ajoute que la somme de tous les ponts menant à chaque région est paire, puisque la moitié de ce nombre est égale au nombre total de ponts. Cependant, cela est impossible s’il y a un nombre impair de masses terrestres avec un nombre impair de ponts. Par conséquent, Euler prouve que s’il y a des nombres impairs attachés à des masses terrestres, il doit y avoir un nombre pair de ces masses terrestres.

Cependant, cela ne suffit pas à prouver lorsqu’il existe un chemin où chaque pont est utilisé une fois et une seule fois, car le problème du pont de Königsberg a un nombre pair de masses terrestres avec un nombre impair de ponts y allant. Pour cette raison, Euler ajoute plus de restrictions aux paragraphes 18 et 19. Euler explique que puisque le total des nombres de ponts attachés à chaque masse terrestre est égal au double du nombre de ponts (comme on le voit dans le lemme de prise de contact), donc si vous ajoutez deux à cette somme puis divisez par deux, vous obtiendrez le nombre total de ponts plus un. Ce nombre est le même que celui utilisé précédemment, qui est utilisé pour dire si un chemin est possible. Si tous les nombres sont pairs, la troisième colonne du tableau totalisera un de moins que le nombre total de ponts plus un.

Euler explique ensuite qu’il est évident que s’il y a deux masses terrestres avec un nombre impair de ponts, le voyage sera toujours possible si le voyage commence dans l’une des régions avec un nombre impair de ponts. En effet, si les nombres pairs sont divisés par deux et que chacun des nombres impairs est augmenté de un et divisé par deux, la somme de ces moitiés sera égale à un de plus que le nombre total de ponts. Cependant, s’il y a quatre masses terrestres ou plus avec un nombre impair de ponts, il est impossible qu’il y ait un chemin. En effet, la somme des moitiés des nombres impairs plus un ainsi que la somme de toutes les moitiés des nombres pairs rendront la somme de la troisième colonne supérieure au nombre total de ponts plus un. Par conséquent, Euler vient de prouver qu’il peut y avoir au plus deux masses terrestres avec un nombre impair de ponts.

Ceci étant dit, Euler peut maintenant tirer ses conclusions sur des formes plus générales du problème du pont de Königsberg. Au paragraphe 20, Euler donne les trois lignes directrices que quelqu’un peut utiliser pour déterminer s’il existe un chemin en utilisant chaque pont une fois et une seule fois. Premièrement, il a affirmé que s’il y a plus de deux masses terrestres avec un nombre impair de ponts, un tel voyage n’est pas possible. Deuxièmement, si le nombre de ponts est impair pour exactement deux masses terrestres, le voyage est possible s’il commence dans l’une des deux masses terrestres impaires. Enfin, Euler déclare que s’il n’y a pas de régions avec un nombre impair de masses terrestres, le voyage peut être accompli à partir de n’importe quelle région. Après avoir énoncé ces trois faits, Euler conclut sa preuve par le paragraphe 21, qui stipule simplement qu’après avoir compris qu’un chemin existe, ils doivent encore faire l’effort d’écrire un chemin qui fonctionne. Euler croyait que la méthode pour y parvenir était triviale, et il ne voulait pas y consacrer beaucoup de temps. Cependant, Euler a suggéré de se concentrer sur la façon de se rendre d’une masse terrestre à l’autre, au lieu de se concentrer sur les ponts spécifiques au début.

La preuve d’Euler et la Théorie des graphes

En lisant la preuve originale d’Euler, on découvre un travail de mathématiques relativement simple et facilement compréhensible; cependant, ce n’est pas la preuve réelle mais les étapes intermédiaires qui rendent ce problème célèbre. La grande innovation d’Euler a été de voir le problème du pont de Königsberg de manière abstraite, en utilisant des lignes et des lettres pour représenter la situation plus vaste des masses terrestres et des ponts. Il a utilisé des lettres majuscules pour représenter les masses terrestres et des lettres minuscules pour représenter les ponts. C’était un tout nouveau type de pensée pour l’époque, et dans son article, Euler a accidentellement déclenché une nouvelle branche des mathématiques appelée théorie des graphes, où un graphe est simplement une collection de sommets et d’arêtes. Aujourd’hui, un chemin dans un graphe, qui contient chaque arête du graphe une fois et une seule fois, est appelé chemin eulérien, à cause de ce problème. Depuis le moment où Euler a résolu ce problème jusqu’à aujourd’hui, la théorie des graphes est devenue une branche importante des mathématiques, qui guide la base de notre réflexion sur les réseaux.

Le problème du pont de Königsberg explique pourquoi Biggs déclare,

Les origines de la théorie des graphes sont humbles, voire frivoles The Les problèmes qui ont conduit au développement de la théorie des graphes n’étaient souvent guère plus que des énigmes, conçues pour tester l’ingéniosité plutôt que pour stimuler l’imagination. Mais malgré la trivialité apparente de ces énigmes, elles ont suscité l’intérêt des mathématiciens, de sorte que la théorie des graphes est devenue un sujet riche en résultats théoriques d’une variété et d’une profondeur surprenantes.

Comme l’indique la déclaration de Biggs, ce problème est si important qu’il est mentionné dans le premier chapitre de chaque livre de théorie des graphes qui a été lu dans la bibliothèque.

Après la découverte d’Euler (ou l’invention, selon la façon dont le lecteur la regarde), la théorie des graphes a connu un essor avec les contributions majeures de grands mathématiciens comme Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff et George Polya. Ces hommes ont tous contribué à découvrir « à peu près tout ce que l’on sait des graphes volumineux mais ordonnés, comme le réseau formé par les atomes dans un cristal ou le réseau hexagonal fabriqué par les abeilles dans une ruche. »D’autres problèmes célèbres de la théorie des graphes incluent trouver un moyen de s’échapper d’un labyrinthe ou d’un labyrinthe, ou trouver l’ordre des mouvements avec un chevalier sur un échiquier de telle sorte que chaque case ne soit posée qu’une seule fois et que le chevalier retourne dans l’espace sur lequel il a commencé. D’autres problèmes de théorie des graphes sont restés non résolus pendant des siècles.

Le destin de Königsberg

Alors que la théorie des graphes a explosé après la résolution du problème du pont de Königsberg par Euler, la ville de Königsberg a connu un destin bien différent. En 1875, les habitants de Königsberg ont décidé de construire un nouveau pont, entre les nœuds B et C, augmentant le nombre de liaisons de ces deux masses terrestres à quatre. Cela signifiait que seules deux masses terrestres avaient un nombre impair de liens, ce qui donnait une solution assez simple au problème. La création du pont supplémentaire peut ou non avoir été inconsciemment causée par le désir d’un chemin pour résoudre le célèbre problème de la ville.

Cependant, un nouveau pont n’a pas résolu tous les problèmes futurs de Königsberg, car la ville ne s’attendait pas au XIXe siècle, « au triste et déchirant destin qui l’attendait comme hôte de l’une des batailles les plus féroces de la Seconde Guerre mondiale. »Pendant quatre jours en août 1944, des bombardiers britanniques ont détruit à la fois la vieille ville et les parties nord de Königsberg. En janvier et février 1945, la région entourant Königsberg est encerclée par les forces russes. Les civils allemands commencent à évacuer la ville, mais se déplacent trop tard. Des milliers de personnes sont tuées en essayant de fuir en bateau et à pied à travers les eaux glacées de la lagune de Courlande. En avril 1945, l’armée rouge capture Königsberg avec environ quatre-vingt-dix pour cent de la vieille ville en ruines.

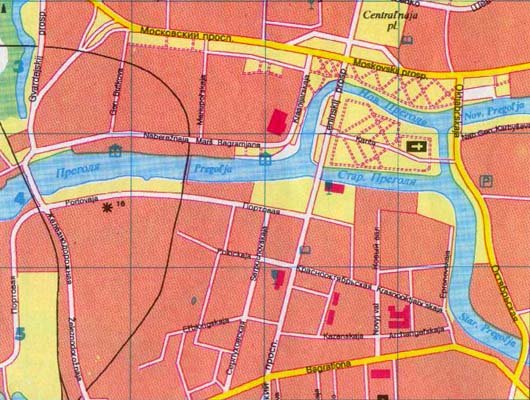
Un plan de rue actuel de Königsberg est fourni ci-dessous. Cette carte montre à quel point la ville a changé. Beaucoup de ponts ont été détruits lors des bombardements, et la ville ne peut plus se poser la même question intrigante qu’au XVIIIe siècle. Avec une disposition très différente, la ville de Königsberg a un nouveau nom, Kaliningrad, avec la rivière Pregel renommée Pregolya. Alors que le sort de Königsberg est terrible, le problème du vieux café des citoyens de traverser chacun de leurs sept anciens ponts exactement une fois a conduit à la formation d’une toute nouvelle branche des mathématiques, la théorie des graphes.

Biggs, Norman L., E. K. Lloyd et Robin J. Wilson. Théorie des graphes : 1736-1936. Il est l’auteur de plusieurs ouvrages.

Dunham, William. Euler : Le Maître de Nous Tous. Washington: La Mathematical Association of America, 1999.

Euler, Leonhard‘ ’Solutio problematis ad geometriam situs pertinentis’ (1741), Eneström 53, Archives MAA Euler.

« Histoire des mathématiques: Sur Leonhard Euler (1707-1783). » ScienceWeek (2003). 6 Novembre 2005.

Hopkins, Brian et Robin Wilson. « La vérité sur Königsberg. »College Mathematics Journal (2004), 35, 198-207.

 » Ponts de Konigsberg. »Les archives de l’histoire des mathématiques MacTutor:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Note de l’éditeur: Cet article a été initialement publié dans Convergence, Volume 3 (2006).