9. Impédance et angle de phase
À ne pas manquer…
Explorez l’impédance, le courant et la tension dans un circuit RLC dans l’applet plus loin sur cette page.
Impédance
L’impédance d’un circuit est la résistance effective totale au flux de courant par une combinaison des éléments du circuit.
Symbole: Z
Unités: `Ω’
La tension totale sur les 3 éléments (résistances, condensateurs et inducteurs) s’écrit
VRLC
Pour trouver cette tension totale, on ne peut pas simplement ajouter les tensions VR, VL et VC.
Parce que VL et VC sont considérés comme des quantités imaginaires, nous avons:
Impédance VRLC=IZ
So ` Z =R+j(X_L− X_C)`
Maintenant, la grandeur (taille ou valeur absolue) de Z est donnée par:
`|Z/=sqrt(R^2+(X_L-X_C)^2`
Angle de phase
‘tan\theta=(X_L-X_C)/R`
L’angle θ représente l’angle de phase entre le courant et la tension.
Comparez cela à l’angle de phase que nous avons rencontré plus tôt dans les graphes de y = a sin (bx + c).
Exemple 1
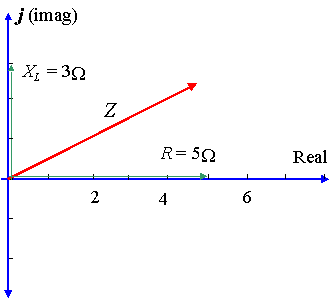
Un circuit a une résistance de `5\Ω` en série avec une réactance sur une inductance de ‘3\Ω’. Représenter l’impédance par un nombre complexe, sous forme polaire.
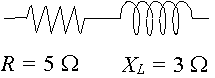
Réponse
Dans ce cas, `X_L =3\Ω` et `X_C=0` donc `X_L-X_C=3\Ω`.
Donc, sous forme rectangulaire, l’impédance s’écrit:
`Z = 5 + 3j\Ω`
À l’aide de la calculatrice, l’amplitude de Z est donnée par: `5.83`, et l’angle `θ` (la différence de phase) est donné par: `30.96^@`.
Donc la tension conduit le courant de ‘30.96 ^@’, comme indiqué dans le diagramme.
En présentant Z comme un nombre complexe (sous forme polaire), on a :
`Z = 5,83 ∠ 30,96^@\Ω’`
Exemple 2(a)
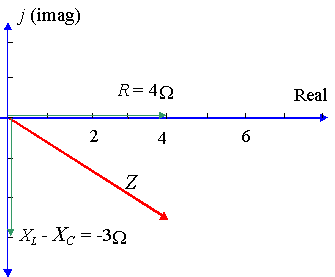
Un circuit alternatif particulier a une résistance de ‘4\Ω’, une réactance sur une inductance de ‘8\Ω’ et une réactance sur un condensateur de `11\Ω’. Exprimer l’impédance du circuit sous forme de nombre complexe sous forme polaire.
Réponse
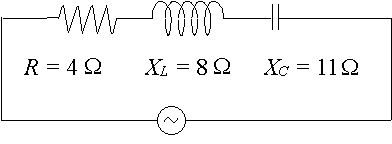
Dans ce cas, nous avons: `X_L-X_C =8-11=-3\Ω`
So `Z =4-3j\Ω` sous forme rectangulaire.
Maintenant pour l’exprimer sous forme polaire:
À l’aide de la calculatrice, on trouve ‘r = 5’ et ‘θ=-36.87^@’.
So `Z=5 ∠-36.87^@\Ω`
Graphique RLC interactif
Voici un graphique interactif avec lequel jouer (ce n’est pas une image statique). Vous pouvez explorer l’effet d’une résistance, d’un condensateur et d’une inductance sur l’impédance totale d’un circuit alternatif.
Activités pour cet interactif
- Tout d’abord, il suffit de jouer avec les curseurs. Vous pouvez:
Faites glisser le curseur supérieur vers la gauche ou la droite pour faire varier l’impédance due à la résistance, `R`,
Faites glisser le curseur XL vers le haut ou vers le bas pour faire varier l’impédance due à l’inducteur, `X_L`, et
Faites glisser le curseur XC vers le haut ou vers le bas pour faire varier l’impédance due au condensateur, `X_C`. - Observez les effets de différentes impédances sur les valeurs de XL-XC et Z.
- Observez les effets des différentes impédances sur θ, l’angle que fait la ligne rouge « résultat » avec l’horizontale (en radians).
- Considérez les graphiques de tension et de courant dans l’interactif. Observez la quantité de retard ou de plomb lorsque vous changez les curseurs.
- Qu’avez-vous appris en jouant avec cet interactif?