2.5: Loi de Darcy – Écoulement en Milieu Poreux
La loi de Darcy est cruciale pour comprendre de nombreuses branches de la géologie, en particulier l’hydrogéologie. Avant d’examiner la loi et ce qu’elle peut nous dire, regardons comment elle a été développée. La loi de Darcy doit son nom à Henry Darcy, un ingénieur français du 19ème siècle qui a développé un système de conduite sous pression souterraine pour acheminer l’eau autour de la ville de Dijon. Le système, qui alimentait également en eau les célèbres fontaines de Dijon, a révolutionné les systèmes d’eau et d’égouts de la ville. Le système ne nécessitait aucune pompe et était entraîné uniquement par gravité. Au cours du processus de développement du nouveau système, Darcy a mené une série d’expériences où il a essayé de déplacer l’eau uniquement en utilisant la gravité.
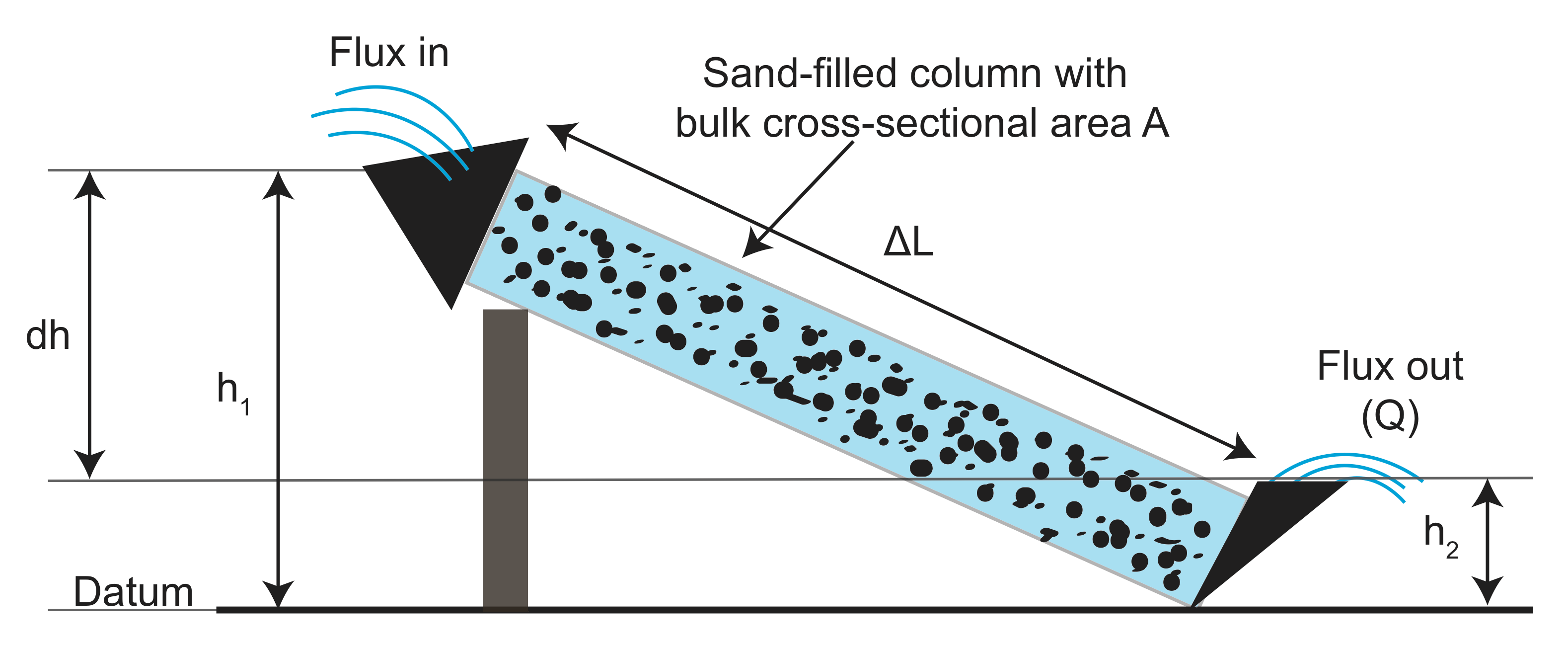
À partir des expériences, les données collectées sur la longueur du canal (\(L \)), la section transversale du canal (\(A \)), la différence de hauteur (\(h_1-h_2 \)) et le flux d’eau sortant \(Q \) avec et sans matériau granulaire (filtrant) dans le flume. Il a ensuite tracé la mesure de flux normalisée par l’aire en fonction du rapport entre la différence de hauteur et la longueur du canal (\(\frac{h_1-h_2}{l}\)). Ce qu’il a trouvé, c’est qu’il y a une relation linéaire, et la pente dépend du matériau granulaire qu’il a utilisé dans le canal:
\
qui peut être réécrit comme une dérivée,
\
où \(K\) est la conductivité hydraulique et \(\frac{dh}{dx}\) est le gradient hydraulique. \(Q\), le débit total, a des unités de \(\frac{m^3}{s}\), le volume d’eau par temps. Le signe négatif est dû au fait que le fluide descend (négatif) le gradient hydraulique de valeurs plus élevées à des valeurs plus basses.
La conductivité hydraulique est un paramètre physique qui explique la facilité avec laquelle le fluide peut se déplacer à travers l’espace poreux du matériau. Dans les expériences originales de Darcy, il a utilisé des sables de différentes tailles de grains, cependant, la conductivité hydraulique peut également être déterminée pour les roches solides, car la plupart des roches ont un espace poreux.
Suite aux expériences originales de Darcy, d’autres travaux ont été effectués pour comprendre les propriétés physiques du fluide et de la roche qui déterminent la conductivité hydraulique efficace. À partir de ces expériences, il a été constaté que,
\
où \(k\) est la perméabilité intrinsèque du milieu poreux (le solide), \(\eta\) est la viscosité dynamique du fluide et \(\gamma= \rho g\) est le poids spécifique du fluide, qui dépend de la densité du fluide, \(\rho\) et de la gravité, \(g\).
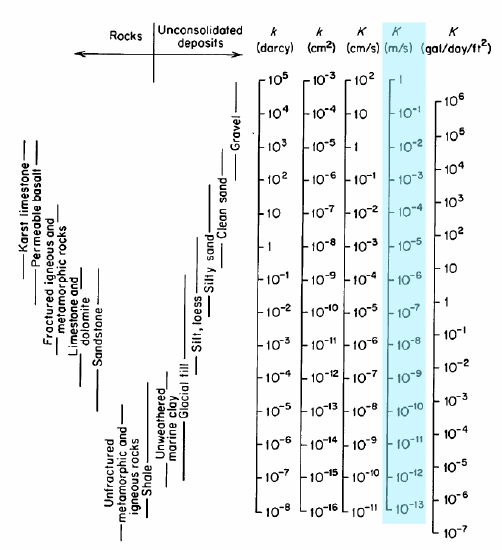
La colonne surlignée sur la figure est K, la conductivité hydraulique en \(\frac{m}{s}\); ce sont les unités que nous utiliserons. La conductivité hydraulique est aussi parfois rapportée en termes de perméabilité intrinsèque, \(k\), avec des unités de darcys ou cm2. La gamme complète de valeurs pour la conductivité hydraulique est 1-10-13\(\frac{m}{s}\). Des expériences comme celles de Darcy sont utilisées pour mesurer K dans des matériaux réels.
Le taux de décharge \ ( Q \) est un flux volumique (\(m ^3 / s \)), mais nous pensons généralement à l’écoulement du fluide en termes de vitesse ou de vitesse. Les questions de décharge peuvent être réorganisées en divisant par l’aire pour définir le flux de Darcy
\\]
Ou en termes de perméabilité intrinsèque et de gradient de pression,
\
où \(\eta\) est la viscosité du fluide (voir ci-dessous pour la dérivation de la deuxième équation).
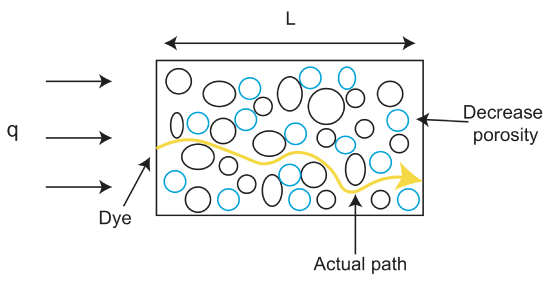
Il est important de noter que le flux de Darcy n’est pas égal à la vitesse du fluide, même s’il est en unités de vitesse. La vitesse du fluide se trouve à travers la vitesse linéaire moyenne (\(v_a\)), qui est la moyenne de la vitesse de tous les trajets possibles du fluide à travers les milieux poreux: mais trouver cette valeur est en dehors de la portée de cette classe. Au lieu de cela, nous noterons que la vitesse du fluide est
\
où \(\varphi\) est la porosité et v est la vitesse du fluide. La porosité, \(\varphi\) est calculée comme le rapport du volume de l’espace vide au volume total d’un matériau \(\varphi = \frac{V_{void}}{V_{tot}} \), et est généralement exprimée en fraction comprise entre 0 et 1 ou en pourcentage. Notez que si \(\varphi\leq\) 1 alors la vitesse du fluide est supérieure au flux de darcy.
Un autre terme qui apparaît lors de la discussion de l’écoulement à travers les roches et les matériaux non consolidés est la perméabilité. Alors que la porosité est la fraction réelle des pores (vides) dans la roche, ces vides peuvent avoir différentes formes et différentes connectivités, ce qui affecte la facilité avec laquelle un fluide peut se déplacer dans l’espace poreux. La perméabilité est une mesure de la facilité avec laquelle les liquides et les gaz peuvent traverser une roche. Plus le matériau est consolidé, plus sa perméabilité est faible. Ainsi, les matériaux « lâches » comme le gravier ont une perméabilité élevée. Certaines roches peuvent également avoir une perméabilité anisotrope, ce qui signifie que les fluides peuvent s’écouler facilement dans une direction, mais pas dans une autre. Un exemple de roche à perméabilité anisotrope est un schiste. Les fluides peuvent se déplacer facilement dans une couche de schiste, mais ne peuvent pas se déplacer à travers les couches.
Vitesse du fluide
Faisons un exemple de base.
On nous donne que \(q = 2 \frac{m}{min}\) et \(\varphi\) est de 25% et que nous voulons trouver la vitesse du fluide.
Nous convertissons d’abord 25% en 0,25.
Alors, \(v = \frac{2}{0.25}\frac{m}{min}\)
et
\(v= 8\frac{m}{min}\) est la vitesse du fluide.
Tête hydraulique
Pour revenir aux expériences de Darcy, quel est le processus physique qui conduit réellement l’écoulement du fluide à travers le canal?
Le terme \(\frac{dh}{dx}\) est appelé la tête hydraulique, qui est la pression du liquide due au poids d’un fluide par rapport à un emplacement de référence: un gradient de pression. Cependant, \(\frac{dh}{dx}\) n’a pas d’unités de pression par unité de longueur, alors pourquoi s’appelle-t-on la tête hydraulique?
Considérons quelle est la pression dans le canal dans les expériences de Darcy. Afin de faire les expériences, Darcy avait un réservoir d’eau à l’extrémité supérieure de la canalisation fournissant un niveau d’eau constant au sommet de la canalisation, équivalent à la hauteur de la canalisation, \(h_1\). De même, il y avait un réservoir au fond avec un niveau d’eau constant équivalent à \(h_2\). Par conséquent, la pression du fluide dans chacun des réservoirs due au poids de l’eau est donnée par \(P = \rho g h\). Le gradient de pression entre le haut et le bas du panache est alors
\
ou
\
En se substituant à la Loi de Darcy,
\&=\frac{K}{\rho g}\frac{dp}{dx}\end{align}. \]
Rappelons, d’en haut, que la conductivité hydraulique peut s’écrire en termes de perméabilité intrinsèque comme \(K=k\frac{\gamma}{\eta}\) ce qui équivaut à \(k\frac{\rho g}{\eta}\) ou à réarranger, \(\frac{K}{\rho g}= \frac{k}{\eta}\). Par conséquent, on peut substituer pour donner deux expressions équivalentes à la Loi de Darcy, avec une interms du gradient en hauteur,
\
et la seconde en termes de gradient de pression,
\
Ainsi, \(\frac{dh}{dx}\) s’appelle la tête hydraulique car l’origine physique du terme dans la Loi de Darcy est le gradient de pression dans le fluide, qui entraîne l’écoulement.
Eau sortant d’un aquifère
Faisons maintenant un exemple de calcul de la vitesse du fluide de l’eau entrant dans un aquifère. Dans le croquis ci-dessous, la hauteur de l’aquifère suit la topographie de la colline adjacente à la vallée avec le ruisseau. L’eau s’écoule de la haute pression (hauteur de la tête) vers la vallée et quitte l’aquifère au niveau du ruisseau. Nous pouvons utiliser la loi de Darcy pour estimer le débit d’eau de l’aquifère.
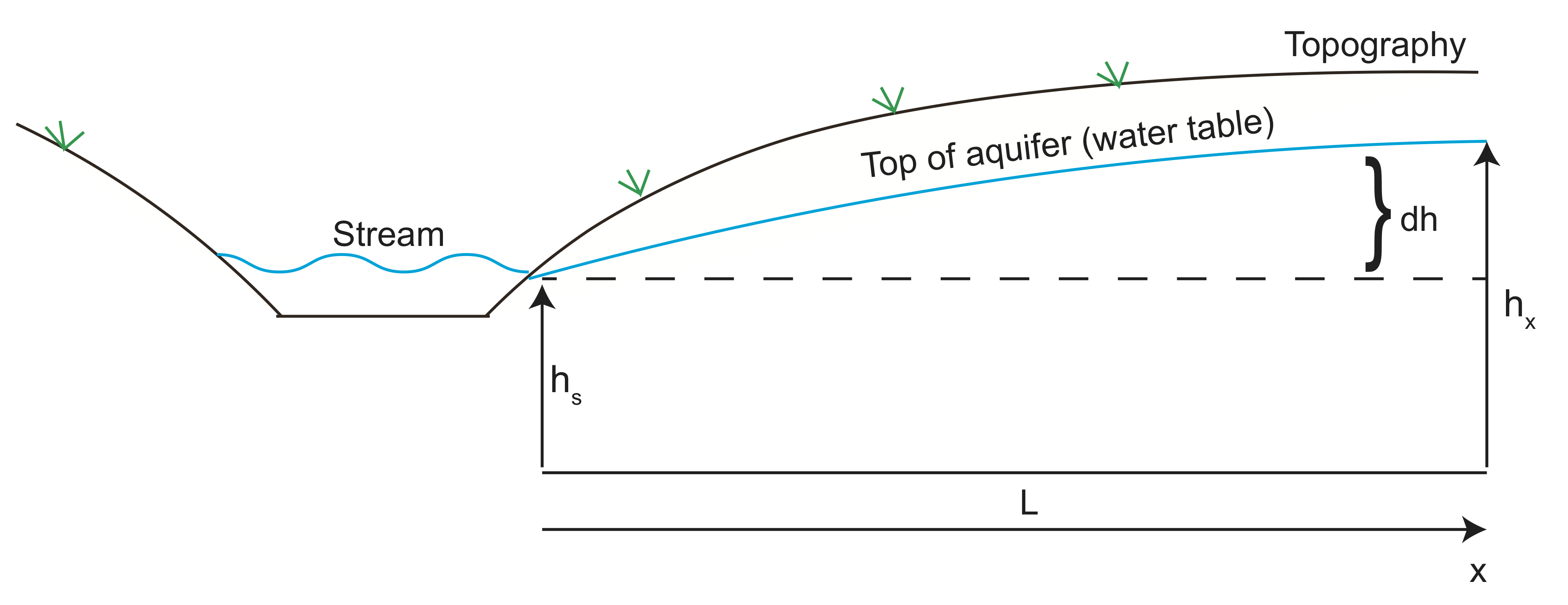
En utilisant l’imagerie géophysique, la hauteur de l’aquifère se trouve à 10 m (\(dh\)) au-dessus de la hauteur du cours d’eau à environ 100 mètres (\(L\)). Supposons que la conductivité hydraulique est \(K = 10 ^{-6} \) m / s et que la porosité est \(\varphi = 30\)%.
Le flux de darcy est
\
\
La vitesse du fluide est
\
\
\
\

Écoulement laminaire versus Écoulement turbulent
Une des hypothèses implicites de la loi de Darcy est que l’écoulement est laminaire. L’écoulement laminaire est caractérisé comme constitué de couches minces ou de lamelles de fluide se déplaçant toutes parallèlement les unes aux autres. En revanche, l’écoulement turbulent est caractérisé par des tourbillons, des tourbillons et des tourbillons, dans lesquels les couches adjacentes de fluide divergent et empruntent des chemins différents vers le bas.
Une façon de quantifier si un fluide est laminaire ou turbulent consiste à calculer le nombre de Reynold pour l’écoulement, défini comme
\
Le nombre de Reynold est trouvé en considérant les deux termes dans le bilan de moment pour l’écoulement. Le premier terme est la force d’inertie par unité de volume, qui entraîne le flux, \(\rho u\frac{du}{dx}\). Le deuxième terme est la force visqueuse par unité de volume, qui résiste à l’écoulement, \(\eta\frac{d^2u}{dx^2} \). Ces deux termes doivent être équilibrés, nous pouvons donc les définir égaux,
\
Ensuite, nous réécrivons les termes, de manière simplifiée pour ne capturer que les dimensions pertinentes des variables. Pour ce faire, nous passons par ce qu’on appelle une analyse dimensionnelle, dans laquelle nous remplaçons chaque variable, par une valeur de référence, fois une forme non dimensionnelle de la variable.
Par exemple pour le terme \(x\) est réécrit comme juste \(L x’\), où \(L\) est la longueur de référence (la profondeur du fluide) et \(x’\) est la distance non dimensionnelle. De même, nous laissons \(u = u_o u ‘\). En les remplaçant dans l’équation, nous obtenons
\
Ensuite, nous combinons les valeurs constantes devant
\
Notez que la combinaison des variables devant est le nombre de Reynold
\
où les variables sont \(u_o\) vitesse d’écoulement, L profondeur du fluide et les variables que nous avons vues précédemment, \(\rho\) densité du fluide et \(\eta\) viscosité du fluide. En parcourant cette analyse, nous constatons que tout écoulement caractérisé par l’équilibre de ces deux termes peut être comparé en connaissant simplement la valeur du nombre de Reynolds. Par exemple, si un flux a une viscosité qui est 10 fois la viscosité dans un autre flux, les deux flux se comporteront de la même manière si la densité (ou la vitesse ou la longueur) est également augmentée d’un facteur 10 pour le cas de viscosité plus élevée; c’est-à-dire que le nombre de Reynolds pour les deux flux est le même.
Pour avoir un flux de Darcy, le nombre de Reynold doit être inférieur à environ 1-10 (laminaire). Pour \(Re > 1-10\) l’écoulement n’est pas strictement laminaire, mais il n’est pas encore turbulent (non linéaire, non laminaire). Pour avoir un écoulement turbulent, le nombre de Reynold doit être supérieur à environ 2000.
Comprendre que les constantes du numérateur et du dénominateur affectent les caractéristiques de l’écoulement de manière opposée, aide également à réfléchir à la façon dont différents fluides se comporteront dans des conditions externes similaires. Par exemple, un fluide plus dense qui a également une vitesse rapide aura un Re plus élevé et présentera un comportement turbulent. En revanche, un fluide tel que la glace qui a une viscosité élevée et se déplace très lentement aura un Re faible et aura probablement un écoulement laminaire. La viscosité élevée de la glace agit pour stabiliser l’écoulement. Comme autre exemple, considérons que deux fluides pourraient tous deux se déplacer à la même vitesse se comporter différemment si les autres valeurs du nombre de Reynold \(\frac {\rho L}{\mu}\) sont différentes. Par conséquent, le type d’écoulement ne dépend pas seulement de la vitesse d’écoulement, mais de la combinaison de variables dans le nombre de Reynold.
Application de l’écoulement de Darcy
La loi de Darcy est la principale équation qui régit l’écoulement dans les aquifères et les puits. Sans cela, nous ne serions pas en mesure de forer des puits ou de comprendre le mouvement de l’eau dans les aquifères, en particulier dans la vallée centrale de la Californie, où ces deux idées sont cruciales pour la productivité agricole et l’affaissement des eaux souterraines.
