in this tutorial, we will learn about Wheatstone Bridge. Näemme toimintaperiaate Wheatstone Bridge, muutamia esimerkkejä piirejä ja joitakin tärkeitä sovelluksia.

Johdatus Wheatstonen siltaan

reaalimaailmassa törmätään erilaisiin signaaleihin, joista osa mitataan resistanssin muutoksilla ja osa induktanssilla ja kapasitanssilla.

Jos otetaan huomioon resistanssi, suurin osa teollisuusantureista kuten lämpötila, rasitus, Kosteus, Siirtymä, nestetaso jne. tuottaa muuttujan muutoksen vastuksen arvon muutoksen. Siksi jokaiselle vastusanturille tarvitaan signaalikäsittely.

yleensä vastusmittaus jaetaan kolmeen tyyppiin, matalan vastuksen mittaukseen, keskiresistanssin mittaukseen ja korkean vastuksen mittaukseen. Jos vastusmittaus on mahdollisesti muutamasta milliohmista mikroohmeihin, niin sitä pidetään matalan vastuksen mittauksena.

tätä mittausta käytetään todellisuudessa tutkimustarkoituksiin. Jos mittaus on 1 ohm 100 k kutsutaan yleensä keskipitkän vastusmittaus. Potentiometri, termistorit jne. mittaus kuuluu tähän luokkaan.

ja erittäin suurta vastusmittausta pidetään 100 kilon ohmista yli 100 mega ohmiin. Vastuksen keskiarvon löytämiseen käytetään erilaisia menetelmiä, mutta enimmäkseen käytetään Wheatstonen siltaa.

mikä on Wheatstonen Silta?

yleisin ja yksinkertaisin vastuksen löytävä siltaverkko on DC Wheatstonen Silta. Tätä siltaa käytetään silloin, kun mitataan pieniä vastusmuutoksia kuten anturisovelluksissa. Tätä käytetään muuntamaan vastusmuutos Muuntimen jännitemuutokseksi.

tämän sillan ja operaatiovahvistimen yhdistelmää käytetään laajasti teollisuudessa erilaisten antureiden ja antureiden osalta. Wheatstone silta koostuu neljästä vastukset, jotka on kytketty muoto timantti tarjonnan lähde ja osoittaa välineitä kuten kuvassa.

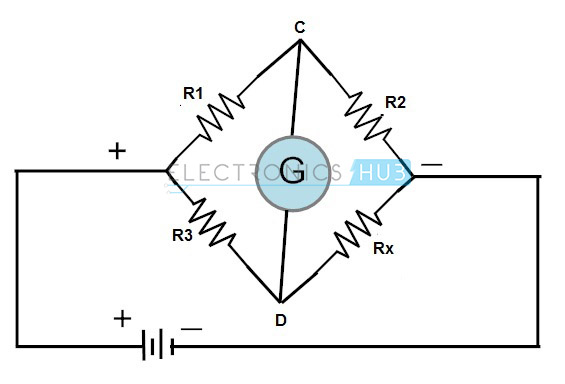
tätä siltaa käytetään tuntemattoman vastuksen etsimiseen hyvin tarkasti vertaamalla sitä vastusten tunnettuun arvoon. Tässä sillassa nollia eli tasapainoista kuntoa käytetään vastuksen etsimiseen.

tällä sillalla tasapainoisen kuntojännitteen pisteissä C ja D on oltava yhtä suuri. Näin ollen galvanometrin läpi ei virtaa mitään virtaa. Saat tasapainoisen kunnossa Yksi vastukset on oltava vaihteleva.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This on ehto sillan tasapainottamiseksi. Ja resistanssin tuntemattoman arvon löytämiseksi

RX = R3 × (R2/R1)

yllä olevasta yhtälöstä R4 tai Rx voidaan laskea resistanssin tunnetusta arvosta R3 ja R2 / R1: n suhteesta. Siksi useimmat tapaukset R2 ja R1 arvot ovat kiinteitä ja R3 arvo on muuttuva niin, että nolla-arvo saavutetaan ja silta saa tasapainossa.

toimintaperiaate

ilman galvanometriä siltapiiri näyttää vain jännitteenjakajapiiriltä, kuten alla olevassa kuvassa on esitetty. Harkitse R1= 20 ohmia, R2= 40 ohmia yhdelle käsivarrelle ja muille harkita samoja arvoja R3 ja R4 vastaavasti.

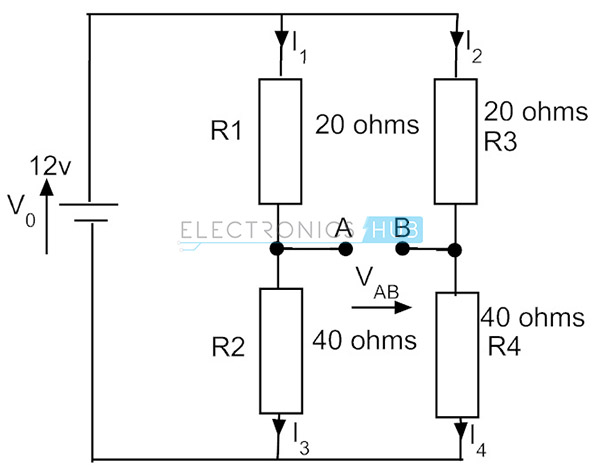
virtaama ensimmäisessä haarassa on

I1 = V/ (R1+R2)

I1 = 12V/ (20+40)

I1 = 0,2 A

ja jännite pisteessä C on yhtä suuri kuin jännitepudotus vastuksessa R2,

VR2 = I1 × R2= 0,2 × 40 = 8v

vastaavasti jännite r1: ssä on 4V (0,2 × 20). Koska samat vastusarvot, Jännitteet R4 ja R3 on sama kuin R1 ja R2 vastaavasti. Näin ollen pisteissä A ja B jännitteet ovat samat, joten galvanometri näyttää nollalukemaa potentiaalieron ollessa nolla. Tällöin sillan sanotaan olevan tasapainoisessa kunnossa.

Oletetaan, että jos toisen varren vastukset käännetään, virtavirta on sama sarjapiiristä johtuen. Mutta jännite koko vastus R4 muuttuu, eli, 0,2 * 20 = 4v. Joten tässä tilassa jännite pisteiden A ja B ovat erilaisia ja olemassa potentiaaliero 8 – 4 = 4v. tämä on epätasapainoinen kunnossa sillan.

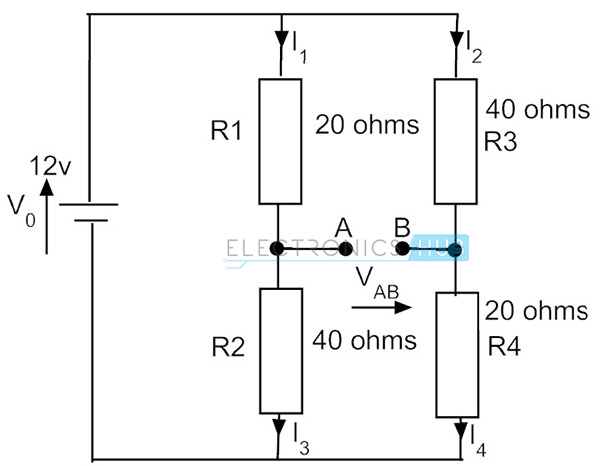
esimerkki Wheatstonen sillasta

ylhäältä, Wheatstonen silta on epätasapainossa, kun volttimittarin lukema ei ole nolla. Lukema voi olla positiivinen tai negatiivinen, riippuu mittarin päätteiden jännitteiden magnitudeista. Tarkastellaanpa alla piiri Wheatstone silta, joka on kytketty löytää tuntematon vastusarvo käyttämällä vastus vuosikymmenen laatikko saada muuttuja vastus R3.

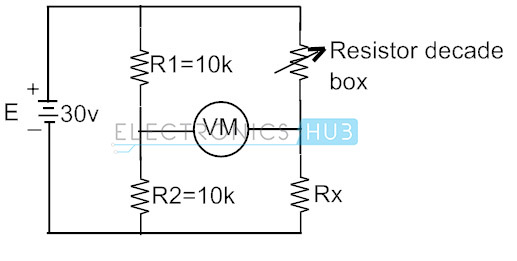
tiedämme, että siltatasapainon ehto on

R4 = R3 × R2 / R1

Rx = RBOX × (10 x 103)/ (10 x 103)

RX = Rbox

tässä tapauksessa Wheatstonen siltaa tasapainotetaan säätämällä vuosikymmenen vastuslaatikkoa, kunnes volttimittari lukee nolla-arvon. Ja vastaava vastusarvo laatikossa on yhtä suuri kuin tuntematon vastus. Oletetaan, jos jännite null ehto tapahtuu 250 ohmia vastus vuosikymmenen laatikko, niin tuntematon vastus on myös 250 ohmia.

Wheatstone Bridge kannan mittaamiseen

yleisimmin kannan mittaamiseen käytetään venymägageja, joiden sähkövastus vaihtelee laitteen suhteellisen kannan mukaan. Käytännössä venymämittarin vastuksen vaihteluväli on 30 ohmista 3000 ohmiin. Tietyn kannan vastusmuutos voi olla vain murto-osa koko alueesta. Siksi käytetään Wheatstone bridge-konfiguraatiota mittaamaan erittäin murto-osa vastusmuutoksista suurella tarkkuudella. Alla olevassa kuvassa on Wheatstonen silta, jossa tuntematon vastus korvataan venymämittarilla.

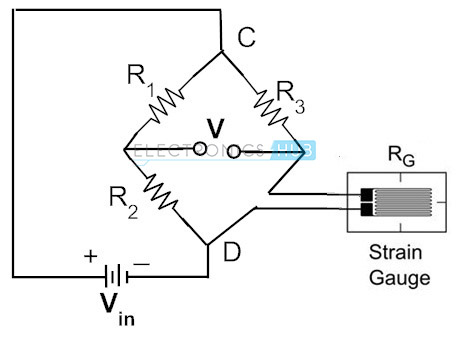
edellä mainitussa piirissä kaksi vastusta R1 ja R2 ovat keskenään yhtä suuret ja R3 on muuttuva vastus. Ilman rasitusta mittari, rheostat on monipuolinen ja lopulta sijoitettu siten, että volttimittari osoittaa nolla taipuma. Tätä kutsutaan sillan tasapainotilaksi. Tämä ehto tarkoittaa, että mittariin ei kohdistu rasitusta.

Jos venymämittari on joko jännittynyt tai puristunut, vastus voi kasvaa tai pienentyä. Siksi tämä aiheuttaa epätasapainoa sillan. Tämä tuottaa jännitteen ilmaisun volttimittarilla vastaa kannan muutosta. Jos venymämittariin kohdistuva kanta on enemmän, mittauspisteiden välinen jännite-ero on suurempi. Jos kanta on nolla, silta tasapainottaa ja mittari näyttää nollalukemaa.

kyse on Vastusmittauksesta, jossa käytetään Wheatstonen siltaa tarkkaan mittaukseen. Vastuksen murto-osan mittauksesta johtuen Wheatstone-siltoja käytetään lähinnä venymämittari-ja lämpömittarimittauksissa.

Sovellukset

1. Wheatstonen siltaa käytetään hyvin alhaisten vastusarvojen tarkkaan mittaamiseen.
2. Wheatstonen siltaa yhdessä operaatiovahvistimen kanssa käytetään fysikaalisten parametrien, kuten lämpötilan, rasituksen, valon jne.mittaamiseen.
3. voimme mitata myös kapasitanssin, induktanssin ja impedanssin suureita Wheatstonen sillan variaatioiden avulla.