regressio keskiarvoon on yleinen tilastollinen ilmiö, joka voi johtaa meitä harhaan tarkkailtaessa maailmaa. Oppiminen tunnistaa, kun regressio keskiarvo on pelissä voi auttaa meitä välttämään väärintulkintaa tietoja ja nähdä malleja, joita ei ole olemassa.

***

on tärkeää minimoida huonon arvostelukyvyn tapaukset ja puuttua päättelymme heikkoihin kohtiin. Se, että opimme taantumaan kohti keskiarvoa, voi auttaa meitä.

Nobel-palkittu psykologi Daniel Kahneman kirjoitti kirjan ennakkoluuloista, jotka sumentavat päättelymme ja vääristävät käsitystämme todellisuudesta. On käynyt ilmi, että on olemassa koko joukko loogisia virheitä, joita teemme, koska intuitiomme ja aivomme eivät käsittele hyvin yksinkertaisia tilastoja. Yksi niistä virheistä, joita hän tutkii ajatellessaan nopeasti ja hitaasti, on surullisen kuuluisa taantuminen kohti keskiarvoa.

käsitteen regressiosta keskiarvoon kehitti ensimmäisenä Sir Francis Galton. Sääntö menee niin, että kaikissa sarjoissa, joissa on monimutkaisia ilmiöitä, jotka ovat riippuvaisia monista muuttujista, joissa sattuma on mukana, äärimmäisiä lopputuloksia seuraa yleensä maltillisemmat.

etsiessään viisautta Peter Bevelin tarjoaa esimerkin Johnista, joka oli tyytymätön uusien työntekijöiden suorituksiin, joten hän laittoi heidät taitoja parantavaan ohjelmaan, jossa hän mittasi työntekijöiden taitoja:

heidän pisteensä ovat nyt korkeammat kuin ensimmäisellä kokeella. Johanneksen johtopäätös: ”taitoa parantava ohjelma paransi taitoa.”Tämä ei välttämättä ole totta. Niiden korkeammat pisteet voivat olla seurausta keskiarvon regressiosta. Koska näiden yksilöiden mitattiin olevan taitoasteikon alapäässä, he olisivat osoittaneet parannusta, vaikka he eivät olisi ottaneet taitoa lisäävää ohjelmaa. Ja heidän aikaisempaan suoritukseensa voi olla monia syitä — stressi, väsymys, sairaus, häiriötekijä jne. Heidän todellinen kykynsä ei ehkä ole muuttunut.

suorituksemme vaihtelee aina jonkin keskimääräisen todellisen suorituksen ympärillä. Äärimmäiset suoritukset menevät yleensä vähemmän äärimmäisiksi seuraavalla kerralla. Miksi? Testimittaukset eivät voi koskaan olla tarkkoja. Kaikki mittaukset koostuvat yhdestä todellisesta osasta ja yhdestä satunnaisvirheosasta. Kun mittaukset ovat äärimmäisiä, ne johtuvat todennäköisesti osittain sattumasta. Sattuman osuus on todennäköisesti pienempi toisella suoritusta mittaavalla kerralla.

jos siirrymme yhdestä tavasta tehdä jotain toiseen vain siksi, että epäonnistumme, on hyvin todennäköistä, että onnistumme seuraavalla kerralla paremmin, vaikka uusi tapa tehdä jotain olisi tasa-arvoinen tai huonompi.

Tämä on yksi syy siihen, että on vaarallista ekstrapoloida pienistä otoskooista, koska aineisto ei välttämättä edusta jakaumaa. Siksi James March myös väittää, että mitä kauemmin joku pysyy työssään, ”sitä pienempi on todennäköinen ero havaitun suoritustiedon ja todellisen kyvykkyyden välillä.”Mitä tahansa voi tapahtua lyhyellä aikavälillä, erityisesti kaikissa ponnisteluissa, joihin liittyy yhdistelmä taitoa ja onnea. (Taidon ja onnen suhde vaikuttaa myös regressioon keskiarvoon.)

regressio keskiarvoon

regression vaikutukset keskiarvoon voidaan usein havaita urheilussa, jossa vaikutus aiheuttaa runsaasti perusteettomia spekulaatioita.

ajatellessaan nopeaa ja hidasta Kahneman muistelee katsoneensa miesten mäkihyppyä, kuria, jossa lopullinen tulos on kahden erillisen hypyn yhdistelmä. Tietoisena taantumisesta keskiarvoon Kahneman hätkähti kuullessaan selostajan ennustukset toisesta hypystä. Hän kirjoittaa:

Norjalla oli loistava ensimmäinen hyppy; hän jännittää, toivoo suojaavansa johtoaan ja pärjää luultavasti huonommin” tai ”Ruotsilla oli huono ensimmäinen hyppy ja nyt hän tietää, ettei hänellä ole mitään menetettävää ja rentoutuu, minkä pitäisi auttaa häntä pärjäämään paremmin.

Kahneman huomauttaa, että kommentoija oli huomannut regression keskiarvoon ja keksinyt tarinan, josta ei ollut kausaalista näyttöä (katso kerronta harhaluulo). Tämä ei tarkoita, etteikö hänen tarinansa voisi olla totta. Ehkä jos mittaisimme sykkeet ennen jokaista hyppyä, näkisimme, että ne ovat rennompia, jos ensimmäinen hyppy oli huono. Siitä ei kuitenkaan ole kyse. Regressio keskiarvoon tapahtuu, kun onnella on merkitystä, kuten ensimmäisen hypyn tuloksessa.

urheilun opetus koskee kaikkea toimintaa, jossa sattumalla on merkitystä. Liitämme usein selityksiä vaikutuksestamme tiettyyn prosessiin sen edistymiseen tai puuttumiseen.

todellisuudessa suoritustiede on monimutkaista, tilanneriippuvaista ja usein suuri osa siitä, mitä ajattelemme olevan hallinnassamme, on todella sattumanvaraista.

mäkihypyssä voimakas tuuli hyppääjää vastaan johtaa siihen, että jopa paras urheilija osoittaa keskinkertaisia tuloksia. Vastaavasti keskinkertaista hyppääjää suosiva kova tuuli ja mäkiolosuhteet voivat johtaa hänen tuloksissaan huomattavaan, mutta väliaikaiseen kolhuun. Nämä vaikutukset kuitenkin häviävät, kun olosuhteet muuttuvat ja tulokset palautuvat normaaliksi.

tällä voi olla vakavia vaikutuksia valmennukseen ja suoritusten seurantaan. Regressiosäännöt viittaavat siihen, että suoritusta tai palkkaamista arvioitaessa on turvauduttava enemmän track Recordsiin kuin erityistilanteiden tuloksiin. Muuten olemme taipuvaisia pettymään.

kun Kahneman oli pitämässä luentoa Israelin ilmavoimille tehokkaan koulutuksen psykologiasta, yksi upseereista kertoi kokemuksestaan, että kehujen ojentaminen alaisilleen johti huonompiin suorituksiin, kun taas toruminen johti parannuksiin myöhemmissä ponnisteluissa. Tämän seurauksena hän oli kasvanut anteliaaksi kielteiselle palautteelle ja alkanut varoa antamasta liikaa kehuja.

Kahneman huomasi heti, että se on taantumassa keskiarvoon töissä. Hän valaisi harhaluuloa yksinkertaisella harjoituksella, jota haluat ehkä kokeilla itse. Hän piirsi ympyrän liitutaululle ja pyysi sitten upseereita yksi kerrallaan heittämään liitukappaleen ympyrän keskelle selkä liitutauluun päin. Tämän jälkeen hän toisti kokeen ja tallensi jokaisen upseerin suoritukset ensimmäisessä ja toisessa kokeessa.

luonnollisesti ne, jotka pärjäsivät uskomattoman hyvin ensimmäisellä yrittämällä, pärjäsivät yleensä huonommin toisella yrittämällä ja päinvastoin. Harhaluulo kävi heti selväksi: suorituksen muutos tapahtuu luonnollisesti. Tämäkään ei tarkoita sitä, että palautteella ei olisi mitään merkitystä – ehkä sillä on, mutta virkailijalla ei ollut mitään todisteita, joiden perusteella se olisi ollut.

epätäydellinen korrelaatio ja sattuma

tässä vaiheessa voi ihmetellä, miksi regressio kohti keskiarvoa tapahtuu ja miten voimme varmistaa, että olemme tietoisia siitä, kun se tapahtuu.

ymmärtääksemme regression keskiarvoon, meidän on ensin ymmärrettävä korrelaatio.

kahden mitan välinen korrelaatiokerroin, joka vaihtelee välillä -1 ja 1, on niiden jakamien tekijöiden suhteellisen painon mitta. Esimerkiksi kahdella ilmiöllä, joilla on vähän yhteisiä tekijöitä, kuten pullotetun veden kulutus ja itsemurhien määrä, korrelaatiokertoimen pitäisi olla lähellä 0: ta. Toisin sanoen, jos tarkastelisimme kaikkia maailman maita ja määrittäisimme tietyn vuoden itsemurhaluvut suhteessa pullotetun veden kulutukseen henkeä kohti, juoni ei näyttäisi lainkaan mallia.

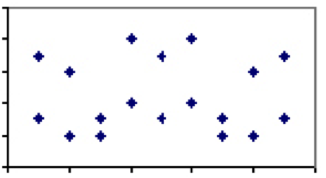
sen sijaan on olemassa toimenpiteitä, jotka ovat yksinomaan riippuvaisia samasta tekijästä. Hyvä esimerkki tästä on lämpötila. Ainoa lämpötilan määräävä tekijä-molekyylien nopeus-on kaikkien asteikkojen yhteinen, joten jokaisella celsiusasteella on täsmälleen yksi vastaava arvo Fahrenheitissa. Siksi lämpötila Celsius ja Fahrenheit on korrelaatiokerroin 1 ja juoni on suora viiva.

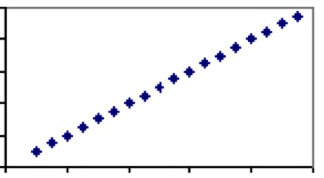
ihmistieteissä on vain vähän jos lainkaan ilmiöitä, joiden korrelaatiokerroin on 1. On kuitenkin paljon tapauksia, joissa yhteys on heikko tai kohtalainen, ja näiden kahden ilmiön välillä on jonkin verran selittävää voimaa. Tarkastellaan pituuden ja painon välistä korrelaatiota, joka laskeutuisi jonnekin 0: n ja 1: n välille. Vaikka käytännössä jokainen kolmevuotias on kevyempi ja lyhyempi kuin jokainen aikuinen mies, eivät kaikki aikuiset miehet tai saman pituiset kolmevuotiaat paina samaa.

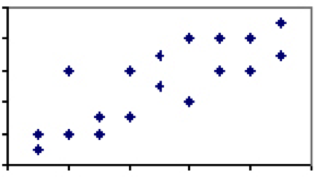
tämä vaihtelu ja sitä vastaava alempi korrelaatioaste viittaa siihen, että vaikka pituus on yleisesti ottaen hyvä ennustaja, pelissä on selvästi muitakin tekijöitä kuin korkeus. Kun kahden toimenpiteen korrelaatio on vähemmän kuin täydellinen, meidän on varottava taantumisen vaikutuksia keskiarvoon.

Kahneman noudatti yleissääntöä: aina kun kahden pistemäärän välinen korrelaatio on epätäydellinen, tapahtuu regressio keskiarvoon.

Tämä saattaa aluksi vaikuttaa sekavalta eikä kovin intuitiiviselta, mutta keskiarvon regressioaste on suoraan verrannollinen muuttujien korrelaatioasteeseen. Tätä vaikutusta voidaan havainnollistaa yksinkertaisella esimerkillä.

oleta olevasi juhlissa ja kysy, mistä johtuu, että erittäin älykkäät naiset tapaavat mennä naimisiin itseään vähemmän älykkäiden miesten kanssa. Useimmat ihmiset, jopa ne, joilla on jonkin verran tilastotieteen koulutusta, hyppäävät nopeasti mukaan erilaisiin kausaalisiin selityksiin, jotka vaihtelevat kilpailun välttämisestä näiden naisten kohtaamiin yksinäisyyden pelkoihin. Tällainen kohun aihe herättänee suurta keskustelua.

nyt, mitä jos kysyttäisiin, miksi puolisoiden älykkyyspisteiden välinen korrelaatio ei ole täydellinen? Tämä kysymys on tuskin yhtä mielenkiintoinen ja on vähän arvata-me kaikki tiedämme tämän olevan totta. Paradoksi on siinä, että nämä kaksi kysymystä sattuvat olemaan algebrallisesti ekvivalentteja. Kahneman selittää:

jos puolisoiden älykkyyden korrelaatio on vähemmän kuin täydellinen (ja jos miehet ja naiset eivät keskimäärin eroa älykkyydeltään), on matemaattinen väistämättömyys, että erittäin älykkäät naiset menevät naimisiin miesten kanssa, jotka ovat keskimäärin vähemmän älykkäitä kuin he ovat (ja päinvastoin, tietenkin). Havaittu regressio keskiarvoon ei voi olla kiinnostavampi tai selitettävämpi kuin epätäydellinen korrelaatio.

olettaen, että korrelaatio on epätäydellinen, kahden partnerin todennäköisyys edustaa ylintä 1%: A jonkin ominaisuuden suhteen on paljon pienempi kuin yhden kumppanin, joka edustaa ylintä 1%: A ja toisen – alinta 99%: a.

syy, seuraus ja hoito

meidän tulisi olla erityisen varovaisia regressiosta keskimääräiseen ilmiöön, kun yritämme määrittää syy-yhteyttä kahden tekijän välillä. Aina kun korrelaatio on epätäydellinen, parhaat näyttävät aina huononevan ja huonoimmat näyttävät paranevan ajan myötä, riippumatta ylimääräisestä hoidosta. Tämä on jotain, mitä yleinen media ja joskus jopa koulutetut tutkijat eivät tunnista.

mieti Kahnemanin antamaa esimerkkiä:

energiajuomalla hoidetut masentuneet lapset paranevat merkittävästi kolmen kuukauden aikana. Keksin tämän lehtiotsikon, mutta se on totta.: jos masentuneita lapsia hoidettaisiin jonkin aikaa energiajuomalla, heidän tilansa paranisi kliinisesti merkittävästi. On myös niin, että masentuneet lapset, jotka viettävät jonkin aikaa seisten päänsä päällä tai halaavat kissaa kaksikymmentä minuuttia päivässä, osoittavat myös paranemista.

aina kun törmää tällaisiin otsikoihin, on hyvin houkuttelevaa tehdä sellainen johtopäätös, että energiajuomat, pään päällä seisominen tai kissojen halaaminen ovat kaikki täysin toteuttamiskelpoisia hoitokeinoja masennukseen. Nämä tapaukset kuitenkin ilmentävät jälleen taantumista keskiarvoon:

masentuneet lapset ovat ääriryhmä, he ovat masentuneempia kuin useimmat muut lapset—ja ääriryhmät taantuvat ajan myötä keskiarvoon. Korrelaatio masennus pisteet peräkkäisissä kertaa testaus on vähemmän kuin täydellinen, joten siellä on taantuminen keskiarvo: masentunut lapset saavat jonkin verran paremmin ajan, vaikka he halaavat ei kissoja ja juoda Red Bull.

usein virheellisesti sanotaan jonkin tietyn politiikan tai hoidon aiheuttavan vaikutuksen, kun ääriryhmien muutos olisi tapahtunut joka tapauksessa. Tämä on perustavanlaatuinen ongelma: mistä voimme tietää, ovatko vaikutukset todellisia vai johtuvatko ne vain vaihtelusta?

onneksi on olemassa tapa erottaa todellinen parannus ja taantuminen keskiarvoon. Se on niin sanotun verrokkiryhmän käyttöönotto, jonka odotetaan paranevan pelkän regression avulla. Tutkimuksen tavoitteena on selvittää, parantaako käsitelty ryhmä enemmän kuin regressio voi selittää.

tosielämän tilanteissa, joissa tiettyjen yksilöiden tai ryhmien suorituskyky on ainoa todellinen vertailukohta, eikä vertailuryhmää voida ottaa käyttöön, regression vaikutuksia voi olla vaikea ellei mahdoton erottaa toisistaan. Voidaan verrata alan keskiarvoon, kohorttiryhmän vertaisiin tai aiempiin parannuslukuihin, mutta mikään näistä ei ole täydellinen mittari.

***

onneksi tietoisuus regressiosta itse keskimääräiseen ilmiöön on jo loistava ensiaskel kohti huolellisempaa lähestymistapaa onnen ja suorituskyvyn ymmärtämiseen.

Jos regressiosta keskiarvoon on jotain opittavaa, niin se on rataennätysten tärkeys sen sijaan, että luotettaisiin kertaluonteisiin menestystarinoihin. Toivon, että kun seuraavan kerran törmäät äärimmäiseen ominaisuuteen, jota osittain ohjaa sattuma, huomaat, että vaikutukset todennäköisesti taantuvat ajan myötä ja muokkaavat odotuksiasi sen mukaisesti.

mitä seuraavaksi kannattaa lukea

• Päivitä ajatteluasi 113 henkisen mallin avulla.
• Lue toisen tason ajattelusta, jotta voit välttää negatiiviset seuraukset.