toimittajan huomautus

Seuraava opiskelijatutkimusraportti laadittiin professori Judit Kardosin Math 255-luokalle, joka pidettiin New Jerseyn Collegessa. Tämä oli 3-opintopisteen johdantokurssin historian matematiikka. Tämä raportti laskettiin 30 prosenttiin lopullisesta arvosanasta. Se on esimerkki sellainen historiallisen tutkimuksen opiskelijat voivat tehdä käyttämällä toissijaisia lähteitä.

Leonard Eulerin ratkaisu Königsbergin Siltaongelmaan

Königsbergin

tarinamme alkaa 1700-luvulta, Preussin viehättävässä Königsbergin kaupungissa Pregeljoen rannalla. Vuonna 1254 Teutonilaiset ritarit perustivat Königsbergin kaupungin Böömin kuninkaan Ottoker II: n johdolla tehtyään toisen ristiretken preussilaisia vastaan. Königsbergistä tuli keskiajalla hyvin tärkeä kaupunki ja kaupan keskus, jonka sijainti oli strategisesti sijoitettu joen rannalle. Kahdeksastoista-luvun taideteokset osoittavat Königsbergin kukoistavana kaupunkina, jossa laivueet täyttävät Pregelin, ja niiden kauppa tarjoaa mukavan elämäntavan sekä paikallisille kauppiaille että heidän perheilleen. Terveen talouden ansiosta kaupunkilaiset pystyivät rakentamaan joen yli seitsemän siltaa, joista suurin osa liittyi Kneiphofin saareen; niiden sijainnit näkyvät oheisesta kuvasta .

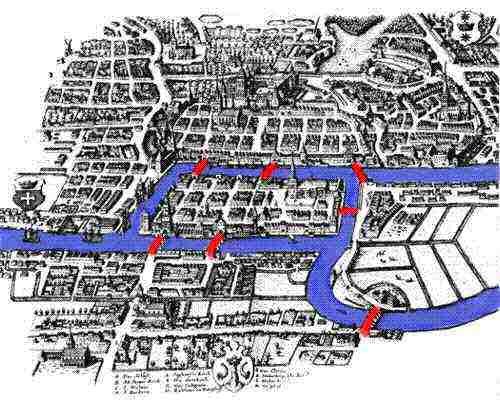
virratessaan Kneiphofin ympäri, tarkoittaen kirjaimellisesti pubin pihaa, ja toisen saaren se jakoi kaupungin neljään erilliseen alueeseen. Seitsemää siltaa kutsuttiin Sepänsillaksi, Yhdyssillaksi, Vihersillaksi, Kauppiasillaksi, Puusillaksi, Korkeasillaksi ja Hunajasillaksi. Tarinan mukaan Königsbergin asukkailla oli tapana viettää sunnuntai-iltapäivät kävellen kauniissa kaupungissaan. Kävellessään kaupungin asukkaat päättivät luoda itselleen pelin, jonka tavoitteena oli keksiä tapa, jolla he voisivat kävellä kaupungin ympäri ylittäen jokaisen seitsemästä sillasta vain kerran. Vaikka kukaan Königsbergin asukkaista ei osannut keksiä reittiä, joka sallisi heidän ylittää jokaisen sillan vain kerran, he eivät silti voineet todistaa, että se oli mahdotonta. Heidän onnekseen Königsberg ei ollut kovin kaukana Pietarista, kuuluisan matemaatikon Leonard Eulerin kotoa.

Euler and The Bridge Problem

miksi Euler vaivaisi itseään ongelmalla, joka ei niin liity matematiikan alaan? Miksi tällainen suuri matemaatikko viettää paljon aikaa triviaali ongelma, kuten Königsbergin sillan ongelma? Euler oli ilmeisesti kiireinen mies, joka julkaisi elinaikanaan yli 500 kirjaa ja papereita. Pelkästään vuonna 1775 hän kirjoitti keskimäärin yhden matemaattisen paperin viikossa, ja hänen elinaikanaan hän kirjoitti useista aiheista matematiikan lisäksi, mukaan lukien mekaniikka, optiikka, tähtitiede, navigointi ja hydrodynamics. Ei ole yllättävää, että Euler piti tätä ongelmaa vähäpätöisenä, todeten vuonna 1736 Danzigin pormestarille Carl Leonhard Gottlieb Ehlerille lähettämässään kirjeessä, joka pyysi häneltä ratkaisua ongelmaan :

. . . Näin näet, useimmat jalo Sir, miten tämän tyyppinen ratkaisu kantaa vähän suhdetta matematiikkaan, ja en ymmärrä, miksi odotat matemaatikko tuottaa sen sijaan kukaan muu, sillä ratkaisu perustuu syy yksin, ja sen löytö ei riipu mitään matemaattista periaatetta. Tämän vuoksi en tiedä, miksi jopa kysymyksiä, jotka kantavat niin vähän suhde matematiikka on ratkaistu nopeammin matemaatikot kuin muut.

vaikka Euler piti ongelmaa triviaalina, se kiehtoi häntä edelleen. Italialaiselle matemaatikolle ja insinöörille Giovanni Marinonille samana vuonna kirjoittamassaan kirjeessä Euler sanoi,

Tämä kysymys on niin banaali, mutta minusta se oli huomion arvoista siinä, että geometria, ei algebra, eikä edes laskemisen taito riittänyt sen ratkaisemiseen.

Euler uskoi, että tämä ongelma liittyi aiheeseen, josta Gottfried Wilhelm Leibniz oli aikoinaan keskustellut ja kaivannut työtä, johon Leibniz viittasi geometriana eli aseman geometriana. Tämä niin sanottu aseman geometria on niin sanottu Graafiteoria, jota Euler esittelee ja hyödyntää ratkaistessaan tätä kuuluisaa ongelmaa.

Eulerin todistus

26.elokuuta 1735 Euler esittää paperin, joka sisältää Konigsbergin siltaongelman ratkaisun. Hän käsittelee sekä tätä erityistä ongelmaa, sekä yleinen ratkaisu, jossa on useita maamassoja ja useita siltoja. Tämä paperi, nimeltään ”Solutio problematis ad geometriam situs pertinentis,” julkaistiin myöhemmin vuonna 1741 . Eulerin paperi on jaettu kaksikymmentäyksi numeroitua kappaletta, ja mitä seuraa, yksinkertaistettu versio Eulerin kappaleet on esitetty.

Eulerin todisteen kahdessa ensimmäisessä kappaleessa hän esittelee Konigsbergin Siltaongelman. Kappaleessa 1 Euler toteaa, että hänen mielestään tämä ongelma koskee geometriaa, mutta ei hänen aikalaistensa hyvin tuntemaa geometriaa, johon kuuluu mittauksia ja laskutoimituksia, vaan uudenlaista geometriaa, johon Leibniz viittasi aseman Geometriana. Sitten kappaleessa 2 Euler selittää yleisölleen, miten Konigsbergin ongelma toimii. Euler edellyttäen luonnos ongelma (KS. Euler n kuva 1), ja kutsutaan seitsemän erillistä sillat: a, b, c, d, e, f, ja, g. tässä kohdassa hän toteaa yleisen kysymyksen ongelma, ”voi selvittää, onko mahdollista ylittää kunkin sillan täsmälleen kerran?”

Eulerin kuviosta 1 ”Solutio problematis ad geometriam situs pertinentis”, Eneström 53

todettuaan yleisen kysymyksen, jota hän yrittää ratkaista, Euler alkaa tutkia erilaisia keinoja ratkaisun löytämiseksi. Kappaleessa 3 Euler kertoo lukijalle, että tämän ongelman ratkaisemiseksi hän voisi kirjoittaa ylös kaikki mahdolliset polut, mutta tämä tekniikka veisi paljon aikaa, eikä toimisi suuremmissa kokoonpanoissa, joissa olisi enemmän siltoja ja maamassoja. Näiden ongelmien vuoksi Euler päätti valita toisen menetelmän ongelman ratkaisemiseksi.

kappaleessa 4 Hän aloittaa ongelman yksinkertaistamisen keksimällä kätevän järjestelmän kuvaamaan sillan ylitystä. Euler päättää, että sen sijaan, että hän käyttäisi pieniä kirjaimia kuvaamaan sillan ylitystä, hän kirjoittaisi suuraakkoset, jotka edustavat maamassoja. Esimerkiksi viittaamalla hänen Kuvioonsa 1 AB merkitsisi matkaa, joka alkoi maamassasta A ja päättyi B. Lisäksi, jos matkustettuaan maamassasta A B joku päättää siirtyä maamassaan D, tämä olisi yksinkertaisesti merkitty, ABD. Kappaleessa 5 Euler jatkaa keskustelua tästä prosessista selittäen, että vaikka ABDC: ssä on neljä isoa kirjainta, vain kolme siltaa ylitettiin. Euler selittää, että riippumatta siitä, kuinka monta siltaa on, on vielä yksi kirjain, joka edustaa tarvittavaa ylitystä. Tämän vuoksi koko Königsbergin Siltaongelma vaati seitsemän sillan ylittämistä ja siten kahdeksan isoa kirjainta.

kappaleessa 6 Euler jatkaa metodinsa yksityiskohtien selittämistä. Hän kertoo lukijalle, että jos on useampia siltoja, jotka voidaan ylittää, kun mennään maamassasta toiseen, ei ole väliä, mitä siltaa käytetään. Vaikka esimerkiksi on olemassa kaksi siltaa, a ja b, jotka voivat viedä kulkijan paikasta A paikkaan B, Eulerin notaatiolla ei ole väliä, kumpi silta on vallattu. Tässä kappaleessa Euler käsittelee myös sitä erityistä ongelmaa, jota hän käsittelee. Hän selittää käyttäen hänen alkuperäinen luku, että Königsbergin ongelma tarvitsee täsmälleen kahdeksan kirjainta,jossa paria (A,B) ja (A, C) on oltava vierekkäin täsmälleen kaksi kertaa, riippumatta siitä, mikä kirjain näkyy ensin. Lisäksi parien (A, D), (B, D) ja (C,D) täytyy esiintyä yhdessä täsmälleen kerran, jotta polku ylittää jokaisen sillan kerran ja on olemassa vain kerran.

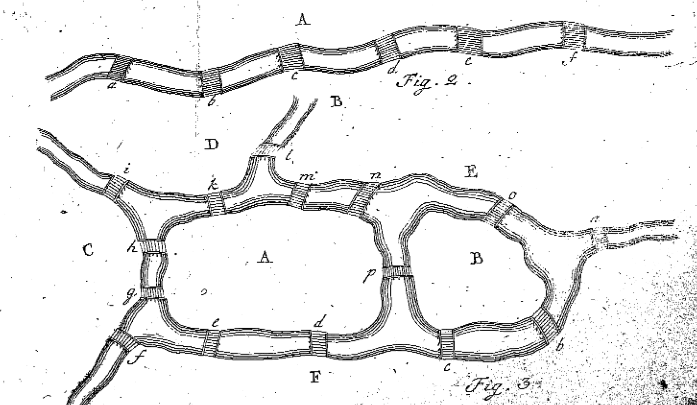
Eulerin luvut 2 ja 3 ”Solutio problematis ad geometriam situs pertinentis”, Eneström 53

kappaleessa 7 Euler ilmoittaa lukijalle, että joko hänen on löydettävä ongelma täyttävä kahdeksan kirjaimen jono, tai hänen on todistettava, ettei tällaista jonoa ole olemassa. Ennen kuin hän tekee tämän Königsbergin sillan ongelma, hän päättää löytää sääntö selvittää, onko polku olemassa yleisempää ongelmaa. Hän tekee tämän 8 kohdassa tarkastelemalla paljon yksinkertaisempia esimerkkejä maamassoista ja silloista. Euler piirtää kuvan 2, ja hän alkaa arvioida tilanteita, joissa alueen A läpi kuljetaan. Euler toteaa, että jos silta a on kulkenut kerran, A oli joko siellä, missä matka alkoi tai päättyi, ja siksi sitä käytettiin vain kerran. Jos kaikki sillat a, b ja c kulkevat kerran, A: ta käytetään täsmälleen kahdesti riippumatta siitä, onko se lähtö-vai loppupaikka. Vastaavasti jos viisi siltaa johtaa A: han, maavalli A esiintyisi matkan aikana tasan kolme kertaa. Euler toteaa, että ” yleensä, jos siltojen lukumäärä on mikä tahansa pariton luku, ja jos sitä lisätään yhdellä, niin A: n esiintymien määrä on puolet tuloksesta.”Toisin sanoen, jos on pariton määrä siltoja, jotka yhdistävät A: n muihin maamassoihin, lisätään yksi siltojen lukumäärään ja jaetaan se kahdella, jotta saadaan selville, kuinka monta kertaa A: ta on yhteensä käytettävä polulla, jossa jokaista siltaa käytetään kerran ja vain kerran (ts. Yhteensä esiintymiä A, jossa A on pariton # siltoja = (# siltoja-1) / 2).

käyttämällä tätä faktaa Euler ratkaisee Königsbergin siltaongelman kappaleessa 9. Siinä tapauksessa, koska on olemassa viisi siltaa, jotka johtavat a, se on tapahduttava kolme kertaa (katso hänen kuva 1, edellä). Samoin, B, C, ja D täytyy näkyä kahdesti, koska ne kaikki on kolme siltaa, jotka johtavat niihin. Näin ollen 3 (A: lle) + 2(B: lle) + 2(C: lle) + 2 (D: lle) = 9, mutta Euler totesi jo, että seitsemälle sillalle saa olla vain kahdeksan esiintymää. Tämä on ristiriitaista! Siksi Königsbergin kaupungin siltoja on mahdotonta kulkea vain kerran. Loppu, vai onko? Vaikka Königsbergin asukkaat voivat olla tyytyväisiä tähän ratkaisuun, suuri matemaatikko Leonhard Euler ei ollut tyytyväinen. Euler jatkaa edelleen hänen todiste käsitellä yleisempiä tilanteita.

Eulerin yleistys

kappaleessa 10 Euler jatkaa keskustelua toteamalla, että jos tilanne koskee kaikkia maamassoja, joissa on pariton määrä siltoja, on mahdollista kertoa, voidaanko matka tehdä käyttämällä jokaista siltaa vain kerran. Euler toteaa, että jos summa, kuinka monta kertaa kunkin kirjaimen täytyy näkyä on yksi enemmän sitten kokonaismäärä siltoja, matka voidaan tehdä. Jos poikkeamia on kuitenkin enemmän kuin yksi enemmän kuin siltoja, matkaa ei voida tehdä, kuten Königsbergin Siltaongelmassa. Tämä johtuu siitä, että sääntö, jonka Euler antaa pariton määrä siltoja käyttäen hänen luku 2, on totta yleinen tilanne, onko olemassa vain yksi muu landmass tai enemmän kuin yksi.

kappaleissa 11 ja 12 Euler käsittelee tilannetta, jossa alueeseen liittyy parillinen määrä siltoja. Tämä tilanne ei näy Königsbergin ongelmassa, joten se on sivuutettu tähän asti. Tilanteessa, jossa on maavalli X, jossa on parillinen määrä siltoja, voi esiintyä kaksi tapausta. Ensimmäinen tapaus on, kun X on lähtöpiste matkalle. Tällöin X esiintyy kahdesti, kerran lähtöpisteenä ja jälleen päätepisteenä. Toisessa tapauksessa X ei ole lähtökohta. Jos näin kävisi, X ilmestyisi paikalle vain kerran, sillä matkan olisi kuljettava yhden sillan kautta ja lähdettävä välittömästi ainoan käytettävissä olevan sillan kautta. Vastaavasti, jos X: ään on kiinnitetty neljä siltaa, X: n esiintymien lukumäärä riippuu siitä, onko se lähtöpiste vai ei. Jos matka alkaa X: stä, sen täytyy näkyä kolme kertaa, mutta jos se ei ala X: stä, se ilmestyy vain kahdesti. Eli yleensä, jos X: ssä on parillinen määrä siltoja kiinnitettynä, niin jos matka ei ala X: ssä, X esiintyy puolet kerrasta siltoina (ts. Esiintymät X, jossa X on parillinen eikä lähtöpiste = (#siltoja) / 2). Jos matka alkaa X: stä, X esiintyy puolet kerroista siltoina plus yksi (eli X: n esiintymät, joissa X on parillinen ja lähtöpiste = ((#silloista) / 2) + 1).

kappaleissa 13-15 Euler selittää, miten selvittää, onko jokaista siltaa käyttävä polku olemassa kerran ja vain kerran, ja esittää oman esimerkkinsä osoittaakseen, miten se toimii. Euler selittää ensin yksinkertaisen kuusiaskelisen menetelmänsä ratkaista mikä tahansa yleinen tilanne jokien jakamilla ja siltojen yhdistämillä maamassoilla. Ensimmäinen Euler tarkoittaa jokaista maamassaa isolla kirjaimella. Toiseksi hän ottaa kokonaislukumäärä siltoja, lisää yksi, ja kirjoittaa tämän edellä kaavion hän on aikeissa tehdä. Seuraavaksi hän ottaa isot kirjaimet, laittaa ne kolumniin ja kirjoittaa niiden viereen siltojen määrän. Neljänneksi hän osoittaa tähdillä maamassat, joissa on parillinen määrä siltoja. Sitten jokaisen parillisen luvun viereen hän kirjoittaa ½ määrästä ja jokaisen parittoman luvun viereen hän sijoittaa ½ luvun plus yhden. Lopuksi Euler lisää oikeaan sarakkeeseen kirjoitetut numerot, ja jos summa on yksi pienempi tai yhtä suuri kuin siltojen lukumäärä plus yksi, vaadittu matka on mahdollinen. On kuitenkin tärkeää huomata, että jos summa on yksi vähemmän kuin siltojen lukumäärä plus yksi, niin matka on aloitettava yhdestä tähdellä merkityistä maamassoista. Jos summa on yhtä suuri kuin siltojen lukumäärä plus yksi, matkan on aloitettava alueelta, jota ei ole merkitty tähdellä.

Examples

Using the Konigsberg problem as his first example Euler shows the following:

siltojen lukumäärä = 7, siltojen lukumäärä plus yksi = 8

Aluesiltojen ajan tulee näkyä

a 5 3

B 3 2

C 3 2

d 3 2

kuitenkin, 3 + 2 + 2 + 2 = 9, joka on enemmän kuin 8, joten matka on mahdoton.

koska tämä esimerkki on melko yksinkertainen, Euler päättää suunnitella oman tilanteensa, jossa on kaksi saarta, neljä jokea ja viisitoista siltaa. Tilanne Euler luotu voidaan nähdä hänen kuva 3, edellä. Euler yrittää nyt selvittää, onko olemassa polku, jonka avulla joku voi mennä jokaisen sillan yli kerran ja vain kerran. Euler noudattaa samoja vaiheita kuin edellä, nimeää viisi eri aluetta isoilla kirjaimilla ja laatii taulukon, jonka avulla se voidaan tarkistaa, jos mahdollista, kuten:

siltojen lukumäärä = 15, siltojen lukumäärä plus yksi = 16

Aluesillat kertaa alueen tulee näkyä

a* 8 4

b* 4 2

c* 4 2

d 3 2

e 5 3

f* 6 3

lisäksi, 4 + 2 + 2 + 2 + 3 + 3 = 16, joka vastaa siltojen määrää plus yksi, eli matka on itse asiassa mahdollinen. Koska summa on yhtä suuri kuin siltojen lukumäärä plus yksi, matkan on aloitettava joko D: stä tai E: stä. Nyt kun Euler tietää, että on mahdollista tehdä matka, hänen tarvitsee vain ilmoittaa, mikä polku tulee olemaan. Euler valitsee polun EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, jossa hän Sisältää, mitkä sillat ylitetään maamassoja edustavien kirjainten välillä. Vaikka nämä tiedot ovat vieraita, koska tarkka silta ei ole väliä tietää, että matka on mahdollista, se on hyödyllinen valittaessa polku. Tämä on hyvä esimerkki, joka osoittaa menetelmän, jota Euler käyttäisi ratkaistessaan mitään tällaista ongelmaa.

Eulerin johtopäätökset

seuraavissa kappaleissa Euler esittää toisen tavan selvittää, voidaanko matka tehdä, kun otetaan huomioon jokin joukko maamassoja, siltoja ja jokia. Euler huomauttaa 16 kohdassa, että suoraan maamassojen oikealle puolelle lueteltujen numeroiden yhteenlaskettu määrä on jopa kaksinkertainen siltojen kokonaismäärään verrattuna. Tätä tosiasiaa aletaan myöhemmin kutsua kädenojennukseksi. Periaatteessa kättelevä lemma toteaa, että jokainen silta lasketaan kaksi kertaa, kerran jokaista maamassaa kohti, johon se on kiinnitetty. Kappaleessa 17 Euler toteaa edelleen, että kaikkien kullekin alueelle johtavien siltojen summa on parillinen, koska puolet tästä määrästä on yhtä suuri kuin siltojen kokonaismäärä. Tämä on kuitenkin mahdotonta, jos on pariton määrä maamassoja, joissa on pariton määrä siltoja. Siksi Euler todistaa, että jos maamassoihin on liitetty parittomia lukuja, näitä maamassoja on oltava parillinen määrä.

tämä ei kuitenkaan riitä todistamaan, milloin on olemassa polku, jossa jokaista siltaa käytetään kerran ja vain kerran, sillä Königsbergin Siltaongelmassa on parillinen määrä maamassoja, joihin menee pariton määrä siltoja. Tämän vuoksi Euler lisää kappaleisiin 18 ja 19 lisää rajoituksia. Euler selittää, että koska yhteenlaskettu määrä siltojen liitteenä kunkin landmass on yhtä suuri kuin kaksinkertainen määrä siltoja (kuten nähdään handshaking heidät), joten siksi, jos lisäät kaksi tähän summaan ja sitten jakaa kahdella, saat määrä yhteensä siltoja plus yksi. Tämä numero on sama kuin aiemmin käytetty numero, jolla kerrotaan, onko polku mahdollinen. Jos kaikki numerot ovat parillisia, taulukon kolmannen sarakkeen summa on yksi vähemmän kuin siltojen kokonaismäärä plus yksi.

Euler selittää tämän jälkeen, että on ilmeistä, että jos on olemassa kaksi maa-aluetta, joissa on pariton määrä siltoja, niin matka on aina mahdollinen, jos matka alkaa joltakin alueelta, jossa on pariton määrä siltoja. Tämä johtuu siitä, että jos parilliset luvut puolitetaan ja jokainen pariton lisätään yhdellä ja puolitetaan, näiden puoliskojen summa vastaa yhtä enemmän kuin siltojen kokonaismäärä. Jos kuitenkin on neljä tai useampia maamassoja, joissa on pariton määrä siltoja, on mahdotonta, että siellä olisi polku. Tämä johtuu siitä, että parittomien lukujen puoliskojen summa plus yksi yhdessä kaikkien parillisten lukujen puoliskojen summan kanssa tekee kolmannen sarakkeen summasta suuremman kuin siltojen yhteenlaskettu lukumäärä plus yksi. Siksi Euler juuri osoittanut, että voi olla enintään kaksi maamassoja pariton määrä siltoja.

tämän todettua Euler voi nyt tehdä johtopäätöksensä Königsbergin Siltaongelman yleisemmistä muodoista. Kappaleessa 20 Euler antaa kolme ohjetta, joiden avulla joku voi selvittää, onko polku olemassa käyttäen jokaista siltaa kerran ja vain kerran. Ensinnäkin hän väitti, että jos on enemmän kuin kaksi maamassoja, joissa on pariton määrä siltoja, niin tällainen matka ei ole mahdollinen. Toiseksi, jos siltojen määrä on pariton tasan kahden maasillan osalta, matka on mahdollinen, jos se alkaa jommastakummasta parittomasta numeroidusta maasillasta. Lopuksi Euler toteaa, että jos ei ole alueita, joilla on pariton määrä maamassoja, matka voidaan suorittaa alkaen miltä tahansa alueelta. Todettuaan nämä kolme tosiasiaa, Euler päättyy hänen todiste 21 kohdassa, jossa yksinkertaisesti todetaan, että kun yksi luvut pois, että polku on olemassa, ne silti täytyy käydä läpi vaivaa kirjoittaa ulos polku, joka toimii. Eulerin mielestä menetelmä tämän saavuttamiseksi oli vähäpätöinen, eikä hän halunnut käyttää siihen paljon aikaa. Euler kuitenkin ehdotti keskittymistä siihen, miten päästä maamassasta toiseen sen sijaan, että keskittyisi ensin tiettyihin siltoihin.

Eulerin todistus-ja Graafiteoria

Eulerin alkuperäistä todistusta lukiessa huomaa suhteellisen yksinkertaisen ja helposti ymmärrettävän matematiikan teoksen; varsinaisen todisteen sijaan välivaiheet tekevät tästä ongelmasta kuuluisan. Eulerin suuri innovaatio oli tarkastella Königsbergin sillan ongelmaa abstraktisti, käyttämällä viivoja ja kirjaimia edustamaan suurempaa tilannetta maamassat ja sillat. Hän käytti isoja kirjaimia edustamaan maamassoja ja pieniä kirjaimia edustamaan siltoja. Tämä oli täysin uudenlaista ajattelua aikaa, ja hänen paperi, Euler vahingossa herätti uuden haaran matematiikan kutsutaan Graafiteoria, jossa kaavio on yksinkertaisesti kokoelma vertices ja reunat. Nykyään graafissa olevaa polkua, joka sisältää graafin jokaisen reunan kerran ja vain kerran, kutsutaan Eulerin poluksi tämän ongelman vuoksi. Siitä lähtien, kun Euler ratkaisi tämän ongelman nykypäivään, graafiteoriasta on tullut tärkeä matematiikan haara, joka ohjaa verkostoja koskevan ajattelumme perustaa.

Königsbergin sillan ongelma johtuu siitä, että Biggsin mukaan

graafiteorian juuret ovat vaatimattomia, jopa kevytmielisiä … graafiteorian kehitykseen johtaneet ongelmat olivat usein vain pulmia, joiden tarkoituksena oli testata kekseliäisyyttä mielikuvituksen stimuloinnin sijaan. Mutta vaikka näennäinen triviality tällaisten palapelit, ne vangittu edun matemaatikot, sillä seurauksella, että Graafiteoria on tullut aihe runsaasti teoreettisia tuloksia yllättävää vaihtelua ja syvyyttä.

kuten Biggsin lausuma antaisi ymmärtää, tämä ongelma on niin tärkeä, että se mainitaan jokaisen kirjastossa käydyn Graafiteoriakirjan ensimmäisessä luvussa.

Eulerin löydön (tai keksinnön, riippuen siitä, miten lukija katsoo sitä) jälkeen Graafiteoria paisui suurten matemaatikkojen, kuten Augustin Cauchyn, William Hamiltonin, Arthur Cayleyn, Gustav Kirchhoffin ja George Polyan, tekemien merkittävien osuuksien myötä. Nämä miehet kaikki auttoivat paljastamaan ” lähes kaiken, mitä tiedetään suurista mutta järjestetyistä kuvioista, kuten kideen atomien muodostaman hilan tai mehiläisten mehiläispesässä tekemän kuusikulmaisen hilan .”Muita kuuluisia graafiteorian ongelmia ovat muun muassa se, että löytää keinon paeta sokkelosta tai labyrintista, tai löytää järjestys, jossa liikkuu ritari shakkilaudalla siten, että jokainen ruutu on laskeutunut vain kerran ja ritari palaa tilaan, josta hän aloitti . Jotkin muut graafiteorian ongelmat ovat jääneet ratkaisematta vuosisatoja .

Königsbergin kohtalo

vaikka Graafiteoria kukoisti Eulerin ratkaistua Königsbergin Siltaongelman, Königsbergin kaupungilla oli paljon erilainen kohtalo. Vuonna 1875 Königsbergin asukkaat päättivät rakentaa uuden sillan solmukohtien B ja C välille, jolloin näiden kahden maa-alueen yhteyksien määrä kasvoi neljään. Tämä tarkoitti sitä, että vain kahdessa maamassassa oli pariton määrä linkkejä, mikä antoi melko suoraviivaisen ratkaisun ongelmaan. Ylimääräisen sillan synty saattoi johtua alitajuisesti siitä, että kaupungin kuuluisaa ongelmaa haluttiin ratkaista polulla.

uusi silta ei kuitenkaan ratkaissut kaikkia Königsbergin tulevia ongelmia, sillä kaupunki ei osannut odottaa 1800-luvulla ”sitä surullista ja sodan runtelemaa kohtaloa, joka sitä odotti isäntänä yhdessä toisen maailmansodan kiivaimmista taisteluista.”Neljän päivän aikana elokuussa 1944 Brittiläiset pommikoneet tuhosivat sekä vanhankaupungin että Königsbergin pohjoisosat. Tammi-helmikuussa 1945 königsbergiä ympäröivä alue joutui venäläisten joukkojen saartamaksi. Saksalaiset siviilit alkavat evakuoida kaupungista, mutta lähtevät liikkeelle liian myöhään. Tuhannet ihmiset saavat surmansa yrittäessään paeta veneillä ja jalkaisin Kuurinmaan laguunin jäisten vesien yli. Huhtikuussa 1945 puna-armeija valtasi Königsbergin noin yhdeksänkymmenen prosentin vanhankaupungin ollessa raunioina.

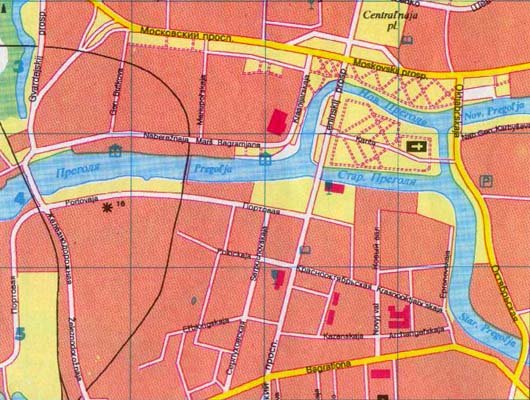
alla on Königsbergin nykyinen katukartta . Tämä kartta näyttää, kuinka paljon kaupunki on muuttunut. Monet sillat tuhoutuivat pommituksissa, ja kaupunki ei voi enää esittää samaa kiehtovaa kysymystä kuin he pystyivät kahdeksastoista-luvulla. Hyvin erilaisen asemakaavan ohella Königsbergin kaupunki on saanut uuden nimen Kaliningrad, jonka Pregel-joki on saanut nimekseen Pregolja . Vaikka Königsbergin kohtalo on karmea, kansalaisten vanhan kahvilan ongelma kulkea kukin vanhasta seitsemästä sillastaan tasan kerran johti täysin uuden matematiikan haaran, graafiteorian, muodostumiseen.

Biggs, Norman L., E. K. Lloyd ja Robin J. Wilson. Graafiteoria: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Meidän kaikkien mestari. Washington: Mathematical Association of America, 1999.

Euler, Leonhard, ”Solutio problematis ad geometriam situs pertinentis” (1741), Eneström 53, MAA Eulerin arkisto.

” Matematiikan historia: on Leonhard Euler (1707-1783).”ScienceWeek” (2003). 6.marraskuuta 2005.

Hopkins, Brian ja Robin Wilson. ”Totuus Königsbergistä.”College Mathematics Journal (2004), 35, 198-207.

”Konigsbergin sillat.”The MacTutor History of Mathematics Archive:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

toimittajan huomautus: Tämä artikkeli on julkaistu alun perin julkaisussa Convergence, Volume 3 (2006).