2.5: Darcyn Lakivirtaus huokoisessa väliaineessa
Darcyn laki on ratkaiseva monien geologian haarojen, erityisesti hydrogeologian ymmärtämisessä. Ennen kuin tarkastelemme lakia ja sitä, mitä se voi kertoa meille, katsotaan, miten se on kehitetty. Darcyn laki on nimetty Henry Darcyn, 1800-luvun ranskalaisen insinöörin mukaan, joka kehitti maanalaisen paineistetun putkijärjestelmän veden toimittamiseksi ympäri Dijonin kaupunkia. Järjestelmä, josta saatiin vettä myös kuuluisiin Dijonin suihkulähteisiin, mullisti kaupungin vesi-ja viemärijärjestelmät. Järjestelmä ei vaatinut pumppuja, ja sitä ajoi puhtaasti painovoima. Uuden järjestelmän kehittelyprosessin aikana Darcy suoritti sarjan kokeita, joissa hän yritti liikuttaa vettä pelkästään painovoiman avulla.
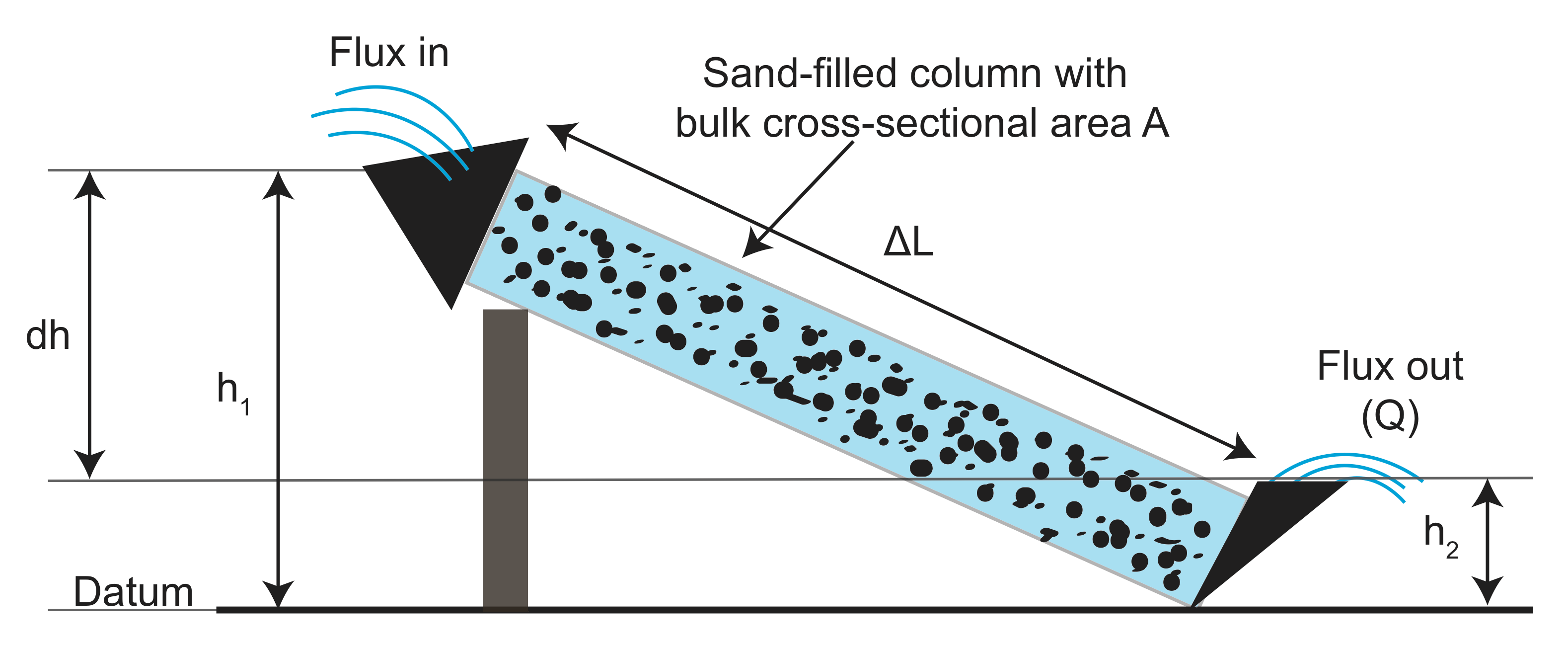
kokeista kerätyt tiedot Savuhormin pituudesta (\(l\)), Savuhormin poikkipinta – alasta (\(a\)), korkeuserosta (\(h_1-h_2\)) ja ulos tulevan veden vuosta \(Q\) sekä rakeisella (suodattavalla) materiaalilla että ilman Flume. Hän sitten piirretään vuon mittaus normalisoitu pinta-ala vs. suhde korkeusero pituus flume (\(\frac{h_1-h_2}{l}\)). Hän havaitsi, että on olemassa lineaarinen suhde, ja kaltevuus riippuu siitä rakeisesta aineesta, jota hän käytti flumessa:
\
, joka voidaan kirjoittaa uudelleen derivaataksi,
\
missä \(k\) on hydraulinen johtavuus ja \(\frac{dh}{dx}\) on hydraulinen gradientti. \(Q\), kokonaispurkausaste, on yksikkönä \(\frac{m^3}{s}\), veden tilavuus kertaa kohti. Negatiivinen merkki johtuu siitä, että neste virtaa alaspäin (negatiivinen) hydraulisen gradientin korkeammista arvoista alhaisempiin arvoihin.
hydraulinen johtavuus on fysikaalinen parametri, joka kertoo, kuinka helposti neste pääsee liikkumaan materiaalin huokosvälin läpi. Darcyn alkuperäisissä kokeissa hän käytti eri raekokoa omaavaa hiekkaa, mutta hydraulinen johtavuus voidaan määrittää myös kiinteille kiville, sillä useimmissa kivissä on jonkin verran huokostilaa.
Darcyn alkuperäisten kokeiden jälkeen tehtiin lisätyötä, jotta ymmärrettäisiin nesteen ja kiven fysikaaliset ominaisuudet, jotka määrittävät tehokkaan hydraulisen johtavuuden. Näistä kokeista selvisi, että
\
missä \(K\) on huokoisen väliaineen (kiinteän aineen) sisäinen permeabiliteetti, \(\eta\) on nesteen Dynaaminen viskositeetti ja \(\gamma = \rho G\) on nesteen ominaispaino, joka riippuu nesteen tiheydestä, \(\Rho\) ja painovoimasta, \(g\).
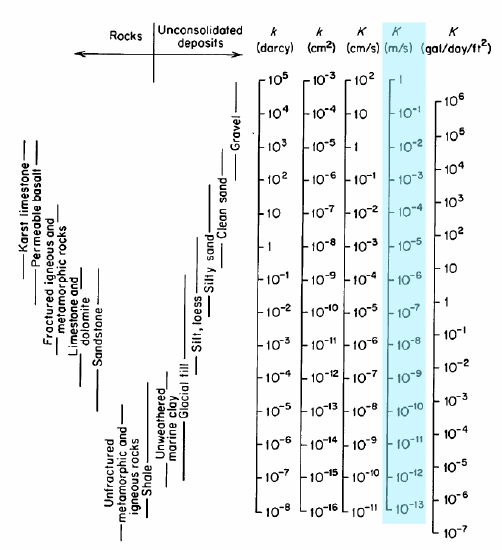
kuvan korostettu sarake on k, hydraulinen johtavuus \(\frac{m}{s}\); näitä yksiköitä käytämme. Hydraulinen johtavuus ilmoitetaan joskus myös sisäisen permeabiliteetin, \(k\), yksikköinä darcys tai cm2. Hydraulisen johtavuuden koko arvoalue on 1-10-13 \(\frac{m}{s}\). Darcyn kaltaisia kokeita käytetään K: n mittaamiseen todellisissa materiaaleissa.
purkausaste \(Q\) on tilavuusvuo (\(m^3/S\)), mutta yleensä ajattelemme fluidin virtausta nopeuden tai nopeuden suhteen. Purkauskysymykset voidaan järjestää uudelleen jakamalla pinta-ala Darcyn vuon määrittelemiseksi
\ \]
tai sisäisen permeabiliteetin ja painegradientin suhteen,
\
missä \(\eta\) on fluidin viskositeetti (katso alla toisen yhtälön derivointi).
on tärkeää huomata, että Darcy flux ei ole yhtä suuri kuin fluidin nopeus, vaikka se on nopeuden yksikköinä. Fluidin nopeus saadaan keskimääräisestä lineaarisesta nopeudesta (\(v_a\)), joka on kaikkien mahdollisten fluidipolkujen nopeuden keskiarvo huokoisen väliaineen läpi: mutta tämän arvon löytäminen ei kuulu tähän luokkaan. Sen sijaan huomaamme, että fluidin nopeus on
\
missä \(\varphi\) on huokoisuus ja v on fluidin nopeus. Huokoisuus \(\varphi\) lasketaan tyhjiöavaruuden tilavuuden suhteena materiaalin kokonaistilavuuteen \(\varphi=\frac{V_{void}}{V_{tot}}\), ja se ilmaistaan yleensä murtolukuna 0: n ja 1: n välillä tai prosentteina. Huomaa, että jos \(\varphi\leq\)1 niin fluidin nopeus on suurempi darcy flux.
toinen termi, joka syntyy puhuttaessa kivien ja sulauttamattomien materiaalien läpivirrasta, on permeabiliteetti. Huokoisuus on Kallion huokosten (tyhjiöiden) todellinen murto-osa, mutta näillä tyhjiöillä voi olla erilaisia muotoja ja erilaisia yhteyksiä, mikä vaikuttaa siihen, kuinka helposti neste voi liikkua huokosten läpi. Läpäisevyys on mitta, jolla nesteet ja kaasut voivat kulkea kiven läpi. Mitä konsolidoidumpi materiaali, sitä pienempi sen läpäisevyys. Siten ”löysä” materiaalit, kuten sora on korkea läpäisevyys. Joillakin kivillä voi olla myös anisotrooppinen läpäisevyys, eli nesteet voivat virrata helposti yhteen suuntaan, mutta eivät toiseen. Esimerkki kivestä, jolla on anisotrooppinen läpäisevyys, on liuskekivi. Nesteet voivat liikkua helposti liuskekerroksen sisällä, mutta eivät voi liikkua kerrosten yli.
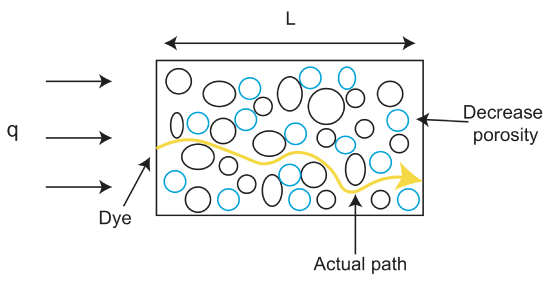
fluidin nopeus
tehdään perusesimerkki.
meille annetaan, että \(q=2\frac{m}{min}\) ja \(\varphi\) on 25% ja haluamme löytää fluidin nopeuden.
ensin muunnetaan 25% 0,25: een.
sitten \(v=\frac{2}{0.25}\frac{m}{min}\)
ja
\(v=8 \frac{m}{min}\) on fluidin nopeus.
hydraulinen Pää
Palatakseni Darcyn kokeisiin, mikä on fysikaalinen prosessi, joka todellisuudessa ohjaa nesteen virtausta hormin läpi?
termillä \(\frac{DH}{dx} \) tarkoitetaan hydraulista päätä, joka on nesteen painosta johtuva nestepaine suhteessa johonkin referenssipaikkaan: painegradienttiin. \(\Frac{DH}{dx} \) ei kuitenkaan sisällä paineyksiköitä pituusyksikköä kohti, joten miksi sitä kutsutaan hydraulipääksi?
pohditaanpa, mikä paine on Darcyn kokeissa. Kokeita varten Darcylla oli vesisäiliö hormin yläpäässä, joka tarjosi tasaisen vedenkorkeuden, joka vastasi hormin korkeutta, \(h_1\). Samoin pohjassa oli säiliö, jonka veden taso oli vakio \(h_2\). Siksi nesteen paine kussakin säiliössä veden painosta on \ (P = \rho g h\). Tällöin painegradientti Plumen ylä-ja alaosan väliltä
\
\
\
korvaa Darcyn lain,
\ & =\frac{k} {\rho g} \frac{dp}{dx} \ end{align}. \]
muista, että hydraulinen johtavuus voidaan kirjoittaa sisäisestä permeabiliteetista \(K = K\frac{\gamma}{\eta}\), joka vastaa \(k\frac{\Rho g}{\eta}\) tai uudelleenjärjestely, \(\frac{k}{\rho g} = \frac{k}{\eta}\). Näin ollen Darcyn laille voidaan antaa kaksi vastaavaa lauseketta, joista toinen on gradientin korkeus,
\
ja toinen paineen gradientin suhteen,
\
näin ollen \(\frac{DH}{dx}\) kutsutaan hydraulipääksi, koska Darcyn lain termin fysikaalinen alkuperä on fluidin painegradientti, joka ohjaa virtausta.
Akviferista lähtevä vesi
tehdään nyt esimerkki, jossa lasketaan veden virtausnopeus akviferiin. Alla olevassa luonnoksessa pohjavesikorkeus seuraa laakson viereisen mäen topografiaa Puron kanssa. Vesi virtaa korkeapaineesta (pään korkeudelta) kohti laaksoa ja jättää pohjavesialueen puron kohdalle. Voimme käyttää Darcyn lakia arvioidaksemme veden virtausnopeutta pohjavesialueella.
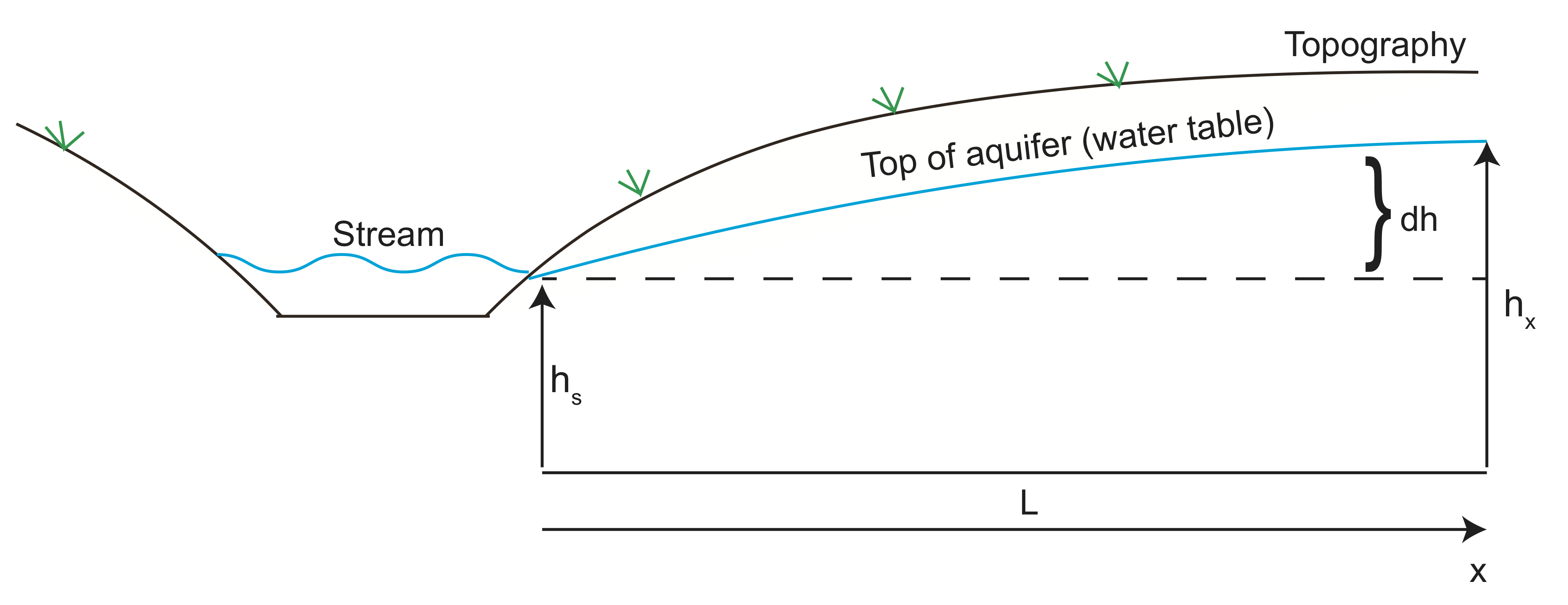
geofysikaalisen kuvantamisen avulla akviferin korkeudeksi todetaan 10 m (\(DH\)) virran korkeudesta noin 100 metrin (\(l\)) päässä. Oletetaan, että hydraulinen johtavuus on \( K=10^{-6}\) m/s ja huokoisuus on \(\varphi=30\)%.
darcy-vuo on
\
\
\
fluidin nopeus on
\
\
\
\

Laminar versus Turbulent Flow
yksi Darcyn lain implisiittisistä oletuksista on, että virtaus on laminaarinen. Laminaarinen virtaus on ominaista koostuu ohuista kerroksista tai laminae nesteen kaikki liikkuvat rinnakkain toisiinsa. Sen sijaan turbulenttista virtausta luonnehtivat pyörteet, pyörteet ja pyörremyrskyt, joissa vierekkäiset nestekerrokset erkanevat ja kulkevat eri polkuja alavirtaan.
yksi tapa määrittää, onko fluidi laminaarinen vai turbulentti, on laskea virtaukselle reynoldin luku, joka määritellään seuraavasti:
\
Reynoldin luku löytyy tarkastelemalla virtauksen liikemomenttitasapainon kahta termiä. Ensimmäinen termi on inertiaalivoima tilavuusyksikköä kohti, joka ohjaa virtausta, \(\rho u\frac{du}{dx}\). Toinen termi on viskoosi voima tilavuusyksikköä kohti, joka vastustaa virtausta, \(\eta\frac{d^2U}{DX^2}\). Näiden kahden termin on oltava tasapainossa, jotta voimme asettaa ne samansuuruisiksi,
\
seuraavaksi kirjoitamme termit uusiksi, yksinkertaistettuna siten, että kuvaamme vain muuttujien merkitykselliset ulottuvuudet. Tehdäksemme käymme läpi niin sanotun dimensioanalyysin, jossa jokainen muuttuja korvataan viitearvolla, kertaa muuttujan ei-dimensionaalisen muodon.
esimerkiksi termi \(x\) kirjoitetaan uudelleen just \(L x’\), jossa \(L\) on viitepituus (fluidin syvyys) ja \(x’\) on ei-ulotteinen etäisyys. Vastaavasti annamme \(u = u_o u’\). Korvaamalla nämä yhtälöön saadaan
\
seuraavaksi yhdistämme vakiot edessä
\
huomaa, että muuttujien yhdistelmä edessä on Reynoldin luku
\
missä muuttujat ovat \(u_o\) virtausnopeus, l fluidin syvyys ja aiemmin näkemämme muuttujat \(\rho\) fluidin tiheys ja \(\eta\) fluidin viskositeetti. Käymällä läpi tämän analyysin, huomaamme, että mikä tahansa virtaus, jolle on ominaista tasapaino näiden kahden ehdon voidaan verrata yksinkertaisesti tietää arvo Reynoldsin luku. Esimerkiksi, jos yksi virtaus on viskositeetti, joka on 10 kertaa viskositeetti toisessa virtaus, kaksi virtaa käyttäytyvät sama on tiheys (tai nopeus tai pituus) on myös lisääntynyt kertoimella 10 korkeamman viskositeetin tapauksessa; toisin sanoen Reynoldsin luku kaksi virtaa on sama.
saadakseen Darcyn virtaamaan Reynoldin luvun täytyy olla alle noin 1-10 (laminaari). \ (Re>1-10 \) virtaus ei ole varsinaisesti laminaarinen, mutta se ei ole vielä turbulentti (epälineaarinen, ei-laminaarinen). Jotta virtaus olisi turbulentti, Reynoldsin luvun on oltava suurempi kuin noin 2000.
ymmärtäminen, että osoittajan ja nimittäjän vakiot vaikuttavat virtauksen ominaisuuksiin päinvastaisella tavalla, auttaa myös miettimään, miten eri fluidit käyttäytyvät samanlaisissa ulkoisissa olosuhteissa. Esimerkiksi tiheämpi neste, joka on myös nopea nopeus on suurempi Re ja näytteille turbulenttista käyttäytymistä. Sen sijaan jään kaltaisella nesteellä, jolla on suuri viskositeetti ja joka liikkuu hyvin hitaasti, on alhainen Re ja todennäköisesti laminaarinen virtaus. Jään korkea viskositeetti vakauttaa virtausta. Toisena esimerkkinä voidaan pitää kahta fluidia, jotka molemmat liikkuvat samalla nopeudella, jotka käyttäytyvät eri tavoin, jos Reynoldin luvun \(\frac{\rho l}{\mu}\) muut arvot ovat erilaiset. Virtaustyyppi ei siis riipu pelkästään virtausnopeudesta, vaan Reynoldin luvun muuttujien yhdistelmästä.
Darcyn virtauksen soveltaminen
Darcyn laki on pääyhtälö, joka säätelee virtausta pohjavesialueilla ja kaivoissa. Ilman sitä emme pystyisi poraamaan kaivoja tai ymmärtämään veden liikettä pohjavesikerroksissa, etenkään Kalifornian central Valleyssa, jossa molemmat ajatukset ovat ratkaisevia sekä maatalouden tuottavuuden että pohjaveden vajoamisen kannalta.
