In diesem Tutorial lernen wir die Wheatstone-Brücke kennen. Wir werden das Arbeitsprinzip der Wheatstone-Brücke, einige Beispielschaltungen und einige wichtige Anwendungen sehen.

Einführung in die Wheatstone-Brücke

In der realen Welt stoßen wir auf verschiedene Signale, von denen einige durch Widerstandsänderungen und einige durch Induktivität und Kapazität gemessen werden.

Wenn wir den Widerstand betrachten, sind die meisten industriellen Sensoren wie Temperatur, Dehnung, Feuchtigkeit, Verdrängung, Flüssigkeitsstand usw. erzeugt die Wertänderung des Widerstands für eine variable Änderung. Daher besteht ein Bedarf an einer Signalaufbereitung für jeden Widerstandssensor.

Im Allgemeinen wird die Widerstandsmessung in drei Typen unterteilt: Messung mit niedrigem Widerstand, Messung mit mittlerem Widerstand und Messung mit hohem Widerstand. Wenn die Widerstandsmessung möglicherweise von einigen Milliohm bis zu Mikroohm reicht, wird sie als Messung mit niedrigem Widerstand angesehen.

Diese Messung wird tatsächlich zu Forschungszwecken verwendet. Wenn die Messung von 1 Ohm bis 100 k ist, wird allgemein als mittlere Widerstandsmessung bezeichnet. Potentiometer, Thermistoren, etc. die Messung fällt unter diese Kategorie.

Und sehr hohe Widerstandsmessung wird von 100 Kilo Ohm bis größer als 100 Mega Ohm betrachtet. Um den mittleren Wert des Widerstands zu finden, werden verschiedene Methoden verwendet, aber meistens wird die Wheatstone-Brücke verwendet.

Was ist die Wheatstone-Brücke?

Das gebräuchlichste und einfachste Brückennetz, um den Widerstand zu finden, ist die DC-Wheatstone-Brücke. Diese Brücke wird dort eingesetzt, wo kleine Widerstandsänderungen wie in Sensoranwendungen gemessen werden sollen. Dies wird verwendet, um eine Widerstandsänderung in eine Spannungsänderung eines Wandlers umzuwandeln.

Die Kombination dieser Brücke mit Operationsverstärker wird in der Industrie ausgiebig für verschiedene Wandler und Sensoren verwendet. Eine Wheatstone-Brücke besteht aus vier Widerständen, die in Form eines Diamanten mit der Versorgungsquelle und den Anzeigeinstrumenten verbunden sind, wie in Abbildung gezeigt.

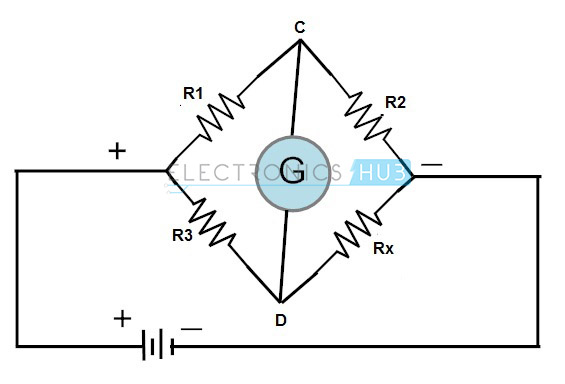
Diese Brücke wird verwendet, um den unbekannten Widerstand sehr genau zu finden, indem sie mit einem bekannten Widerstandswert verglichen wird. In dieser Brücke wird null oder symmetrischer Zustand verwendet, um den Widerstand zu finden.

Für diesen Brückenausgleich muss die Spannung an den Punkten C und D gleich sein. Daher fließt kein Strom durch das Galvanometer. Um den symmetrischen Zustand zu erhalten, muss einer der Widerstände variabel sein.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This ist die Bedingung, um die Brücke auszugleichen. Und um den unbekannten Wert des Widerstands zu finden

RX = R3 × (R2 / R1)

Aus der obigen Gleichung R4 oder Rx kann aus dem bekannten Wert des Widerstands R3 und dem Verhältnis von R2/R1 berechnet werden. Daher sind in den meisten Fällen die Werte R2 und R1 fest und der Wert R3 variabel, so dass ein Nullwert erreicht wird und die Brücke ausgeglichen wird.

Arbeits Prinzip

Ohne die galvanometer, die brücke schaltung sieht nur wie eine spannung teiler schaltung wie in der abbildung unten gezeigt. Betrachten Sie R1 = 20 Ohm, R2 = 40 Ohm für einen Arm und für den anderen die gleichen Werte von R3 und R4.

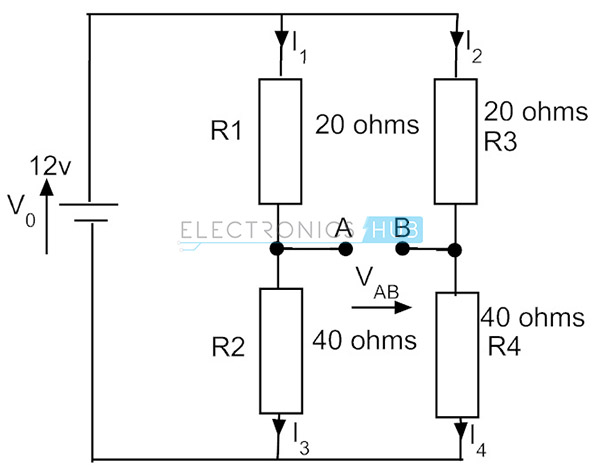
Stromfluss in erste arm ist

I1 = V/(R1 + R2)

I1 = 12 V/(20 + 40)

I1 = 0.2 A

Und die Spannung am Punkt C ist gleich dem Spannungsabfall am Widerstand R2,

VR2 = I1 × R2= 0.2 × 40 = 8V

In ähnlicher Weise beträgt die Spannung an R1 4V 0,2 × 20). Aufgrund der gleichen Widerstandswerte sind die Spannungen an R4 und R3 gleich denen von R1 bzw. R2. Daher sind an den Punkten A und B die Spannungen gleich, daher zeigt das Galvanometer einen Nullwert an, da die Potentialdifferenz Null ist. In diesem Fall soll sich die Brücke in einem ausgeglichenen Zustand befinden.

Angenommen, wenn wir die Widerstände im zweiten Arm umkehren, ist der Stromfluss aufgrund der Reihenschaltung gleich. Die Spannung am Widerstand R4 ändert sich jedoch, d. H. 0,2 * 20 = 4 V. In diesem Zustand sind die Spannungen an den Punkten A und B unterschiedlich und es besteht eine Potentialdifferenz von 8 – 4 = 4 V. Dies ist der unsymmetrische Zustand der Brücke.

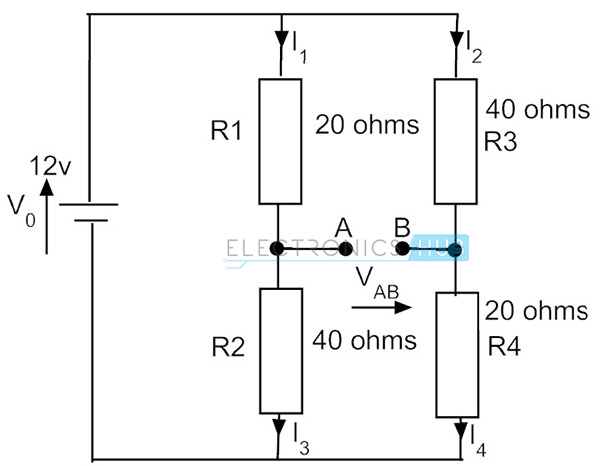
Beispiel einer Wheatstone-Brücke

Von oben ist die Wheatstone-Brücke unsymmetrisch, wenn der Voltmeterwert nicht Null ist. Dieser Messwert kann positiv oder negativ sein, abhängig von den Größen der Spannungen an den Zähleranschlüssen. Betrachten wir die folgende Schaltung der Wheatstone-Brücke, die angeschlossen ist, um den unbekannten Widerstandswert unter Verwendung der Widerstandsdekade zu ermitteln, um den variablen Widerstand von R3 zu erhalten.

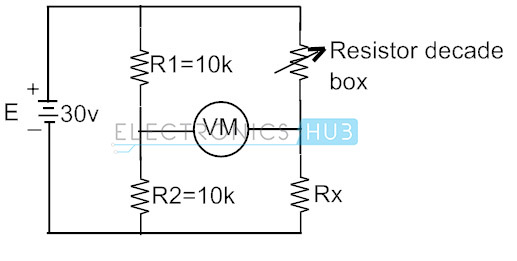
Wir wissen, dass die Bedingung für das Brückengleichgewicht

R4 = R3 × R2 / R1

Rx = RBOX × (10 x 103)/ (10 x 103)

Rx = RBOX

Hier in diesem Fall wird die Wheatstone-Brücke durch Einstellen der Dekadenwiderstandsbox ausgeglichen, bis das Voltmeter den Nullwert anzeigt. Und der entsprechende Widerstandswert in der Box ist gleich dem unbekannten Widerstand. Angenommen, wenn die Spannungsnullbedingung bei 250 Ohm der Widerstandsdekade auftritt, beträgt der unbekannte Widerstand ebenfalls 250 Ohm.

Wheatstone-Brücke zur Dehnungsmessung

Am häufigsten werden zur Messung der Dehnung Dehnungsmessstreifen verwendet, deren elektrischer Widerstand mit der proportionalen Dehnung im Gerät variiert. In der Praxis reicht der Bereich des Dehnungsmessstreifen-Widerstands von 30 Ohm bis 3000 Ohm. Für eine gegebene Dehnung kann die Widerstandsänderung nur einen Bruchteil des gesamten Bereichs betragen. Um daher nur einen Bruchteil der Widerstandsänderungen mit hoher Genauigkeit zu messen, wird eine Wheatstone-Brückenkonfiguration verwendet. Die folgende Abbildung zeigt die Wheatstone-Brücke, bei der der unbekannte Widerstand durch einen Dehnungsmessstreifen ersetzt wird.

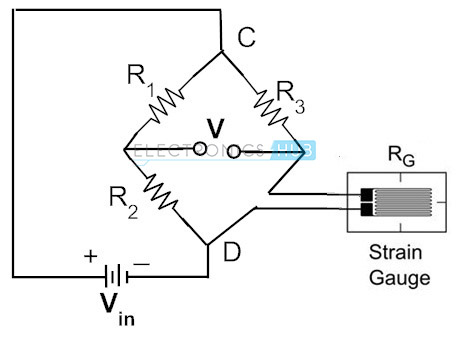
In der obigen Schaltung sind zwei Widerstände R1 und R2 gleich und R3 ist der variable Widerstand. Da keine Kraft auf den Dehnungsmessstreifen ausgeübt wird, wird der Rheostat variiert und schließlich so positioniert, dass das Voltmeter eine Durchbiegung von Null anzeigt. Dies wird als Brückenausgleichsbedingung bezeichnet. Diese Bedingung stellt dar, dass das Messgerät nicht belastet wird.

Wenn der Dehnungsmessstreifen entweder gespannt oder komprimiert ist, kann sich der Widerstand erhöhen oder verringern. Dies führt daher zu einer Unwucht der Brücke. Dies erzeugt eine Spannungsanzeige, die der Dehnungsänderung entspricht. Wenn die auf einen Dehnungsmessstreifen aufgebrachte Dehnung größer ist, ist die Spannungsdifferenz zwischen den Zähleranschlüssen größer. Wenn die belastung null ist, dann die brücke salden und meter zeigt null lesen.

Hier geht es um die Widerstandsmessung mit einer Wheatstone-Brücke zur präzisen Messung. Aufgrund der fraktionierten Widerstandsmessung werden Wheatstone-Brücken meist in Dehnungsmessstreifen- und Thermometermessungen verwendet.

Anwendungen

1. Die Wheatstone-Brücke dient zur präzisen Messung der sehr niedrigen Widerstandswerte.
2. Wheatstone-Brücke zusammen mit Operationsverstärker wird verwendet, um die physikalischen Parameter wie Temperatur, Dehnung, Licht usw. zu messen.
3. Wir können auch die Größen Kapazität, Induktivität und Impedanz mit den Variationen auf der Wheatstone-Brücke messen.