Anmerkung des Herausgebers

Der folgende studentische Forschungsbericht wurde für Professor Judit Kardos ‚Math 255-Klasse am College of New Jersey erstellt. Dies war ein 3-Kredit-Einführungskurs in die Geschichte der Mathematik. Dieser Bericht wurde auf 30% der Abschlussnote angerechnet. Es ist ein Beispiel für die Art der historischen Forschung Studenten mit sekundären Quellen tun können.

Leonard Eulers Lösung des Königsberger Brückenproblems

Königsberg

Unsere Geschichte beginnt im 18. 1254 gründeten Deutsche Ritter unter der Führung des böhmischen Königs Ottoker II. nach ihrem zweiten Kreuzzug gegen die Preußen die Stadt Königsberg. Im Mittelalter wurde Königsberg mit seiner strategisch günstigen Lage am Fluss zu einer sehr wichtigen Stadt und Handelszentrum. Kunstwerke aus dem achtzehnten Jahrhundert zeigen Königsberg als blühende Stadt, in der Flotten von Schiffen den Pregel füllen, und ihr Handel bietet sowohl den lokalen Händlern als auch ihren Familien einen komfortablen Lebensstil. Die gesunde Wirtschaft ermöglichte es den Einwohnern der Stadt, sieben Brücken über den Fluss zu bauen, von denen die meisten mit der Insel Kneiphof verbunden waren.

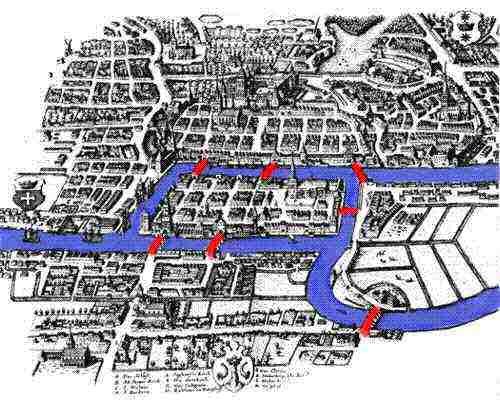
Als der Fluss um den Kneiphof und eine weitere Insel floss, teilte er die Stadt in vier verschiedene Regionen. Die sieben Brücken wurden Schmiedebrücke, Verbindungsbrücke, Grüne Brücke, Kaufmannsbrücke, Holzbrücke, Hochbrücke und Honigbrücke genannt. Der Überlieferung nach verbrachten die Bürger von Königsberg Sonntagnachmittage damit, durch ihre schöne Stadt zu spazieren. Ihr Ziel war es, einen Weg zu finden, wie sie durch die Stadt laufen und jede der sieben Brücken nur einmal überqueren können. Obwohl keiner der Bürger von Königsberg eine Route erfinden konnte, die es ihnen ermöglichte, jede der Brücken nur einmal zu überqueren, konnten sie dennoch nicht beweisen, dass dies unmöglich war. Zum Glück war Königsberg nicht weit von St. Petersburg entfernt, der Heimat des berühmten Mathematikers Leonard Euler.

Euler und das Brückenproblem

Warum sollte sich Euler mit einem Problem befassen, das nichts mit dem Gebiet der Mathematik zu tun hat? Warum sollte ein so großer Mathematiker viel Zeit mit einem trivialen Problem wie dem Königsberger Brückenproblem verbringen? Euler war offensichtlich ein vielbeschäftigter Mann, der zu Lebzeiten mehr als 500 Bücher und Papiere veröffentlichte. Allein 1775 schrieb er durchschnittlich ein mathematisches Papier pro Woche, und zu Lebzeiten schrieb er über eine Vielzahl von Themen neben der Mathematik, darunter Mechanik, Optik, Astronomie, Navigation und Hydrodynamik. Es ist nicht verwunderlich, dass Euler dieses Problem für trivial hielt und in einem Brief von 1736 an Carl Leonhard Gottlieb Ehler, Bürgermeister von Danzig, der ihn um eine Lösung des Problems bat:

. . . Sie sehen also, edler Herr, daß diese Art von Lösung wenig mit der Mathematik zu tun hat, und ich verstehe nicht, warum Sie erwarten, daß ein Mathematiker sie vor allen anderen hervorbringt, denn die Lösung beruht allein auf der Vernunft, und ihre Entdeckung hängt von keinem mathematischen Prinzip ab. Deshalb weiß ich nicht, warum selbst Fragen, die so wenig mit Mathematik zu tun haben, von Mathematikern schneller gelöst werden als von anderen.

Obwohl Euler das Problem trivial fand, war er immer noch fasziniert. In einem Brief, der im selben Jahr an Giovanni Marinoni, einen italienischen Mathematiker und Ingenieur, geschrieben wurde, sagte Euler:

Diese Frage ist so banal, schien mir aber in dieser Hinsicht Aufmerksamkeit zu verdienen Geometrie, noch Algebra, noch die Kunst des Zählens reichten aus, um sie zu lösen.

Euler glaubte, dass dieses Problem mit einem Thema zusammenhängt, das Gottfried Wilhelm Leibniz einmal diskutiert hatte und mit dem er arbeiten wollte, etwas, das Leibniz als geometria situs oder Geometrie der Position bezeichnete. Diese sogenannte Geometrie der Position ist das, was jetzt Graphentheorie genannt wird, die Euler einführt und nutzt, während dieses berühmte Problem zu lösen.

Eulers Beweis

Am 26.August 1735 legt Euler ein Papier vor, das die Lösung des Königsberger Brückenproblems enthält. Er adressiert sowohl dieses spezifische Problem als auch eine allgemeine Lösung mit beliebig vielen Landmassen und beliebig vielen Brücken. Dieses Papier, genannt ‚Solutio problematis ad geometriam situs pertinentis‘, wurde später im Jahre 1741 veröffentlicht . Eulers Papier ist in einundzwanzig nummerierte Absätze unterteilt, und im Folgenden wird eine vereinfachte Version von Eulers Absätzen vorgestellt.

In den ersten beiden Absätzen von Eulers Beweis führt er das Königsberger Brückenproblem ein. In Absatz 1 gibt Euler an, dass er glaubt, dass dieses Problem die Geometrie betrifft, aber nicht die Geometrie, die seinen Zeitgenossen gut bekannt ist und Messungen und Berechnungen beinhaltet, sondern eine neue Art von Geometrie, die Leibniz als Geometrie der Position bezeichnete. Dann erklärt Euler in Absatz 2 seinem Publikum, wie das Königsberg-Problem funktioniert. Euler lieferte eine Skizze des Problems (siehe Eulers Abbildung 1) und nannte die sieben verschiedenen Brücken: a, b, c, d, e, f und g. In diesem Absatz stellt er die allgemeine Frage des Problems: „Kann man herausfinden, ob es möglich ist, jede Brücke genau einmal zu überqueren?“

Eulers Abbildung 1 aus ‚Solutio problematis ad geometriam situs pertinentis‘, Eneström 53

Nachdem Euler die allgemeine Frage gestellt hat, die er zu lösen versucht, beginnt er, verschiedene Methoden zu erforschen, um eine Lösung zu finden. In Absatz 3 sagt Euler dem Leser, dass er zur Lösung dieses spezifischen Problems alle möglichen Pfade aufschreiben könnte, aber diese Technik würde viel Zeit in Anspruch nehmen und würde nicht für größere Konfigurationen mit mehr Brücken und Landmassen funktionieren. Aufgrund dieser Probleme entschied sich Euler für eine andere Methode zur Lösung dieses Problems.

In Absatz 4 beginnt er, das Problem zu vereinfachen, indem er ein praktisches System erfindet, um die Überquerung einer Brücke darzustellen. Euler entscheidet, dass er anstelle der Kleinbuchstaben, die die Überquerung einer Brücke darstellen, die Großbuchstaben schreiben würde, die die Landmassen darstellen. Zum Beispiel, unter Bezugnahme auf seine Figur 1, AB würde eine Reise bedeuten, die in Landmasse A begann, und endete in B.. Außerdem, wenn nach der Reise von Landmasse A nach B, Jemand beschließt, nach Landmasse D zu ziehen, Dies würde einfach bezeichnet werden, ABD. In Absatz 5 setzt Euler seine Diskussion über diesen Prozess fort und erklärt, dass in ABDC, obwohl es vier Großbuchstaben gibt, nur drei Brücken überquert wurden. Euler erklärt, dass es, egal wie viele Brücken es gibt, einen weiteren Buchstaben geben wird, der die notwendige Kreuzung darstellt. Aus diesem Grund erforderte das gesamte Königsberger Brückenproblem die Überquerung von sieben Brücken und damit acht Großbuchstaben.

In Absatz 6 erläutert Euler weiterhin die Details seiner Methode. Er sagt dem Leser, wenn es mehr als eine Brücke gibt, die überquert werden kann, wenn man von einer Landmasse zur anderen geht, spielt es keine Rolle, welche Brücke benutzt wird. Obwohl es beispielsweise zwei Brücken gibt, a und b, die einen Reisenden von A nach B bringen können, spielt es bei Eulers Notation keine Rolle, welche Brücke genommen wird. In diesem Abschnitt geht Euler auch auf das spezifische Problem ein, mit dem er es zu tun hat. Er erklärt anhand seiner Originalfigur, dass das Königsberger Problem genau acht Buchstaben benötigt, wobei die Paare (A, B) und (A, C) genau zweimal nebeneinander erscheinen müssen, egal welcher Buchstabe zuerst erscheint. Darüber hinaus müssen die Paare (A, D), (B, D) und (C, D) genau einmal zusammen vorkommen, damit ein Pfad, der jede Brücke einmal und nur einmal überquert, existiert.

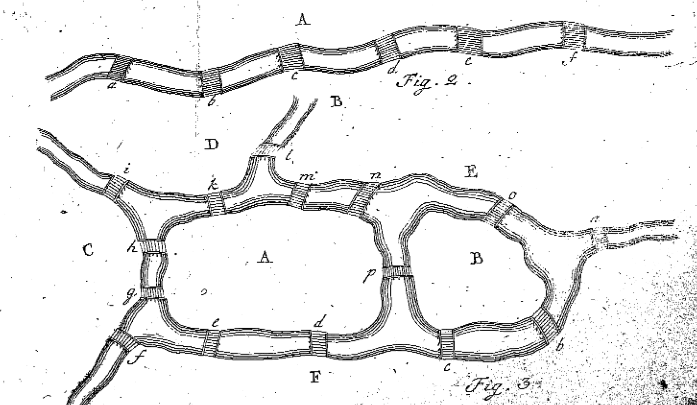
Eulers Abbildungen 2 und 3 aus „Solutio problematis ad geometriam situs pertinentis“, Eneström 53

In Absatz 7 informiert Euler den Leser, dass er entweder eine Acht-Buchstaben-Sequenz finden muss, die das Problem erfüllt, oder er muss beweisen, dass keine solche Sequenz existiert. Bevor er dies für das Königsberger Brückenproblem tut, beschließt er, eine Regel zu finden, um herauszufinden, ob ein Pfad für ein allgemeineres Problem existiert. Er tut dies in Absatz 8, indem er sich ein viel einfacheres Beispiel für Landmassen und Brücken ansieht. Euler zeichnet Abbildung 2 und beginnt, die Situationen zu bewerten, in denen Region A durchlaufen wird. Euler stellt fest, dass, wenn die Brücke a einmal befahren wird, A entweder dort war, wo die Reise begann oder endete, und daher nur einmal verwendet wurde. Wenn die Brücken a, b und c alle einmal befahren werden, wird A genau zweimal verwendet, unabhängig davon, ob es sich um den Start- oder Endort handelt. In ähnlicher Weise würde, wenn fünf Brücken zu A führen, die Landmasse A genau dreimal auf der Reise auftreten. Euler sagt: „Im Allgemeinen, wenn die Anzahl der Brücken eine ungerade Zahl ist, und wenn sie um eins erhöht wird, dann ist die Anzahl der Vorkommen von A die Hälfte des Ergebnisses.“ Mit anderen Worten, wenn es eine ungerade Anzahl von Brücken gibt, die A mit anderen Landmassen verbinden, addieren Sie eine zur Anzahl der Brücken und dividieren Sie sie durch zwei, um herauszufinden, wie oft insgesamt A im Pfad verwendet werden muss, wobei jede Brücke einmal und nur einmal verwendet wird (d. H. Gesamtzahl der Vorkommen von A, wobei A eine ungerade Anzahl von Brücken hat = (anzahl der Brücken – 1) / 2).

Mit dieser Tatsache löst Euler das Königsberger Brückenproblem in Absatz 9. Da es in diesem Fall fünf Brücken gibt, die zu A führen, muss dies dreimal vorkommen (siehe Abbildung 1 oben). In ähnlicher Weise müssen B, C und D zweimal erscheinen, da sie alle drei Brücken haben, die zu ihnen führen. Daher ist 3 (für A) + 2 (für B) + 2 (für C) + 2 (für D) = 9, aber Euler hat bereits gesagt, dass es für die sieben Brücken nur acht Vorkommen geben muss. Das ist ein Widerspruch! Daher ist es unmöglich, die Brücken in der Stadt Königsberg einmal und nur einmal zu befahren. Das Ende, oder ist es? Während die Königsberger mit dieser Lösung zufrieden sein mögen, war der große Mathematiker Leonhard Euler nicht zufrieden. Euler setzt seinen Beweis fort, sich mit allgemeineren Situationen zu befassen.

Eulers Verallgemeinerung

In Absatz 10 setzt Euler seine Diskussion fort, indem er feststellt, dass, wenn die Situation alle Landmassen mit einer ungeraden Anzahl von Brücken betrifft, festgestellt werden kann, ob eine Reise mit jeder Brücke nur einmal unternommen werden kann. Euler sagt, dass, wenn die Summe der Anzahl der Male, die jeder Buchstabe erscheinen muss, eins mehr ist als die Gesamtzahl der Brücken, eine Reise gemacht werden kann. Wenn jedoch die Anzahl der Vorkommnisse größer als eins mehr als die Anzahl der Brücken ist, kann keine Reise unternommen werden, wie das Königsberger Brückenproblem. Dies liegt daran, dass die Regel, die Euler für eine ungerade Anzahl von Brücken mit seiner Abbildung 2 angibt, für die allgemeine Situation gilt, unabhängig davon, ob es nur eine andere Landmasse oder mehr als eine gibt.

In den Paragraphen 11 und 12 befasst sich Euler mit der Situation, dass eine Region eine gerade Anzahl von Brücken hat. Diese Situation tritt im Königsberger Problem nicht auf und wurde daher bisher ignoriert. In der Situation mit einer Landmasse X mit einer geraden Anzahl von Brücken können zwei Fälle auftreten. Der erste Fall ist, wenn X der Ausgangspunkt für die Reise ist. In diesem Fall erscheint X zweimal, einmal als Startpunkt und erneut als Endpunkt. Im anderen Fall ist X nicht der Ausgangspunkt. Wenn dies geschehen würde, würde X nur einmal erscheinen, da die Reise durch eine Brücke eintreten und sofort durch die einzige andere verfügbare Brücke verlassen müsste. Wenn an X vier Brücken angeschlossen sind, hängt die Anzahl der Vorkommen von X davon ab, ob es sich um einen Ausgangspunkt handelt oder nicht. Wenn die Reise in X beginnt, muss sie dreimal erscheinen, aber wenn sie nicht in X beginnt, würde sie nur zweimal erscheinen. Wenn also X eine gerade Anzahl von Brücken angehängt hat, erscheint X, wenn die Reise nicht in X beginnt, im Allgemeinen halb so oft wie Brücken (d. H. Vorkommen von X, wobei X gerade ist und nicht der Startpunkt = (anzahl der Brücken) / 2). Wenn die Reise in X beginnt, erscheint X halb so oft wie Brücken plus eins (dh Vorkommen von X, wobei X gerade ist und Startpunkt = ((anzahl der Brücken) / 2) + 1).

In den Absätzen 13 bis 15 erklärt Euler, wie man herausfindet, ob ein Pfad mit jeder Brücke einmal und nur einmal existiert, und präsentiert sein eigenes Beispiel, um zu zeigen, wie es funktioniert. Euler erklärt zunächst seine einfache sechsstufige Methode, um jede allgemeine Situation mit Landmassen zu lösen, die durch Flüsse geteilt und durch Brücken verbunden sind. Der erste Euler bezeichnet jede Landmasse mit einem Großbuchstaben. Zweitens nimmt er die Gesamtzahl der Brücken, fügt eine hinzu und schreibt diese über das Diagramm, das er erstellen wird. Als nächstes nimmt er die Großbuchstaben, legt sie in eine Spalte und schreibt daneben die Anzahl der Brücken. Viertens zeigt er mit Sternchen die Landmassen an, die eine gerade Anzahl von Brücken haben. Dann schreibt er neben jede gerade Zahl ½ der Zahl und neben jede ungerade Zahl setzt er ½ die Zahl plus eins. Schließlich fügt Euler die Zahlen in der Spalte ganz rechts hinzu, und wenn die Summe eins kleiner oder gleich der Anzahl der Brücken plus eins ist, ist die erforderliche Reise möglich. Es ist jedoch wichtig zu beachten, dass, wenn die Summe eins weniger als die Anzahl der Brücken plus eins ist, die Reise von einer der mit einem Sternchen gekennzeichneten Landmassen aus beginnen muss. Wenn die Summe der Anzahl der Brücken plus eins entspricht, muss die Reise in einer Region beginnen, die nicht mit einem Sternchen gekennzeichnet ist.

Beispiele

Mit dem Königsberg-Problem als erstes Beispiel zeigt Euler Folgendes:

Anzahl der Brücken = 7, Anzahl der Brücken plus eins = 8

Region Brücken Mal Region Muss erscheinen

A 5 3

B 3 2

C 3 2

D 3 2

, 3 + 2 + 2 + 2 = 9, das ist mehr als 8, also ist die Reise unmöglich.

Da dieses Beispiel ziemlich einfach ist, beschließt Euler, seine eigene Situation mit zwei Inseln, vier Flüssen und fünfzehn Brücken zu entwerfen. Die Situation, die Euler geschaffen hat, ist in seiner Abbildung 3 oben zu sehen. Euler versucht nun herauszufinden, ob es einen Weg gibt, der es jemandem erlaubt, jede Brücke einmal und nur einmal zu überqueren. Euler folgt den gleichen Schritten wie oben, benennt die fünf verschiedenen Regionen mit Großbuchstaben und erstellt eine Tabelle, um zu überprüfen, ob dies möglich ist, wie folgt:

Anzahl der Brücken = 15, Anzahl der Brücken plus eins = 16

Regionsbrücken Mal Region Muss erscheinen

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

Zusätzlich, 4 + 2 + 2 + 2 + 3 + 3 = 16, das entspricht der Anzahl der Brücken plus eins, was bedeutet, dass die Reise tatsächlich möglich ist. Da die Summe der Anzahl der Brücken plus eins entspricht, muss die Fahrt entweder in D oder E beginnen. Jetzt, da Euler weiß, dass es möglich ist, eine Reise zu machen, muss er nur noch angeben, wie der Weg aussehen wird. Euler wählt den Pfad EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, wo er einschließt, welche Brücken zwischen den Buchstaben gekreuzt werden, die die Landmassen darstellen. Während diese Informationen fremd sind, da die genaue Brücke keine Rolle spielt, wenn man weiß, dass eine Reise möglich ist, ist es nützlich, wenn man einen Pfad auswählt. Dies ist ein gutes Beispiel, das die Methode zeigt, die Euler bei der Lösung eines Problems dieser Art verwenden würde.

Eulers Schlussfolgerungen

In den nächsten Absätzen stellt Euler eine weitere Möglichkeit vor, um herauszufinden, ob eine Reise mit Landmassen, Brücken und Flüssen unternommen werden kann. In Ziffer 16 weist Euler darauf hin, dass die Summe der Zahlen, die direkt rechts von den Landmassen aufgeführt sind, das Doppelte der Gesamtzahl der Brücken ergibt. Diese Tatsache wird später als Handshaking-Lemma bekannt. Grundsätzlich besagt das Handshaking-Lemma, dass jede Brücke zweimal gezählt wird, einmal für jede Landmasse, an die sie angeschlossen ist. In Ziffer 17 führt Euler weiter aus, dass die Summe aller Brücken, die zu jeder Region führen, gerade ist, da die Hälfte dieser Zahl der Gesamtzahl der Brücken entspricht. Dies ist jedoch unmöglich, wenn es eine ungerade Anzahl von Landmassen mit einer ungeraden Anzahl von Brücken gibt. Daher beweist Euler, dass es eine gerade Anzahl dieser Landmassen geben muss, wenn ungerade Zahlen an Landmassen gebunden sind.

Dies reicht jedoch nicht aus, um zu beweisen, wenn es einen Pfad gibt, auf dem jede Brücke nur einmal benutzt wird, da das Königsberger Brückenproblem eine gerade Anzahl von Landmassen mit einer ungeraden Anzahl von Brücken hat, die zu ihnen führen. Aus diesem Grund fügt Euler in den Absätzen 18 und 19 weitere Einschränkungen hinzu. Euler erklärt, dass, da die Gesamtzahl der an jede Landmasse angehängten Brücken gleich der doppelten Anzahl von Brücken ist (wie im Handshake-Lemma zu sehen), wenn Sie also zwei zu dieser Summe addieren und dann durch zwei dividieren, Sie erhalten die Anzahl der Gesamtbrücken plus eins. Diese Nummer ist die gleiche wie die zuvor verwendete, die verwendet wird, um festzustellen, ob ein Pfad möglich ist. Wenn alle Zahlen gerade sind, beträgt die dritte Spalte in der Tabelle eins weniger als die Gesamtzahl der Brücken plus eins.

Euler erklärt dann, dass es offensichtlich ist, dass, wenn es zwei Landmassen mit einer ungeraden Anzahl von Brücken gibt, die Reise immer möglich ist, wenn die Reise in einer der Regionen mit einer ungeraden Anzahl von Brücken beginnt. Dies liegt daran, wenn die geraden Zahlen halbiert werden und jede der ungeraden um eins erhöht und halbiert wird, entspricht die Summe dieser Hälften einer weiteren als der Gesamtzahl der Brücken. Wenn es jedoch vier oder mehr Landmassen mit einer ungeraden Anzahl von Brücken gibt, ist es unmöglich, dass es einen Pfad gibt. Dies liegt daran, dass die Summe der Hälften der ungeraden Zahlen plus eins zusammen mit der Summe aller Hälften der geraden Zahlen die Summe der dritten Spalte größer macht als die Gesamtzahl der Brücken plus eins. Daher hat Euler gerade bewiesen, dass es höchstens zwei Landmassen mit einer ungeraden Anzahl von Brücken geben kann.

Damit kann Euler nun seine Schlussfolgerungen zu allgemeineren Formen des Königsberger Brückenproblems ziehen. In Absatz 20 gibt Euler die drei Richtlinien an, anhand derer jemand herausfinden kann, ob ein Pfad existiert, indem er jede Brücke einmal und nur einmal verwendet. Erstens behauptete er, wenn es mehr als zwei Landmassen mit einer ungeraden Anzahl von Brücken gibt, dann ist keine solche Reise möglich. Zweitens, wenn die Anzahl der Brücken für genau zwei Landmassen ungerade ist, ist die Reise möglich, wenn sie in einer der beiden ungeraden Landmassen beginnt. Schließlich stellt Euler fest, dass, wenn es keine Regionen mit einer ungeraden Anzahl von Landmassen gibt, die Reise in jeder Region beginnen kann. Nachdem Euler diese drei Tatsachen dargelegt hat, schließt er seinen Beweis mit Paragraph 21 ab, der einfach besagt, dass man, nachdem man herausgefunden hat, dass ein Pfad existiert, immer noch die Anstrengung unternehmen muss, einen Pfad aufzuschreiben, der funktioniert. Euler glaubte, dass die Methode, dies zu erreichen, trivial war, und er wollte nicht viel Zeit damit verbringen. Euler schlug jedoch vor, sich darauf zu konzentrieren, wie man von einer Landmasse zur anderen kommt, anstatt sich zunächst auf die spezifischen Brücken zu konzentrieren.

Eulers Beweis und Graphentheorie

Wenn man Eulers Originalbeweis liest, entdeckt man ein relativ einfaches und leicht verständliches mathematisches Werk; es ist jedoch nicht der eigentliche Beweis, sondern die Zwischenschritte, die dieses Problem berühmt machen. Eulers große Innovation bestand darin, das Königsberger Brückenproblem abstrakt zu betrachten, indem Linien und Buchstaben verwendet wurden, um die größere Situation von Landmassen und Brücken darzustellen. Er verwendete Großbuchstaben, um Landmassen darzustellen, und Kleinbuchstaben, um Brücken darzustellen. Dies war eine völlig neue Art des Denkens für die Zeit, und in seinem Papier, Euler löste versehentlich einen neuen Zweig der Mathematik namens Graphentheorie, wo ein Graph ist einfach eine Sammlung von Ecken und Kanten. Heutzutage wird ein Pfad in einem Diagramm, der jede Kante des Diagramms nur einmal enthält, aufgrund dieses Problems als Eulerscher Pfad bezeichnet. Von der Zeit, als Euler dieses Problem löste, bis heute ist die Graphentheorie zu einem wichtigen Zweig der Mathematik geworden, der die Grundlage unseres Denkens über Netzwerke bildet.

Das Problem der Königsberger Brücke ist, warum Biggs sagt ,

Die Ursprünge der Graphentheorie sind bescheiden, sogar frivol … Die Probleme, die zur Entwicklung der Graphentheorie führten, waren oft wenig mehr als Rätsel, die eher den Einfallsreichtum als die Phantasie anregen sollten. Trotz der offensichtlichen Trivialität solcher Rätsel erregten sie das Interesse der Mathematiker, so dass die Graphentheorie zu einem Thema geworden ist, das reich an theoretischen Ergebnissen von überraschender Vielfalt und Tiefe ist.

Wie Biggs ‚Aussage implizieren würde, ist dieses Problem so wichtig, dass es im ersten Kapitel jedes graphentheoretischen Buches erwähnt wird, das in der Bibliothek gelesen wurde.Nach Eulers Entdeckung (oder Erfindung, je nachdem, wie der Leser es betrachtet) boomte die Graphentheorie mit wichtigen Beiträgen großer Mathematiker wie Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff und George Polya. Diese Männer trugen alle dazu bei, „so ziemlich alles aufzudecken, was über große, aber geordnete Graphen bekannt ist, wie das Gitter, das von Atomen in einem Kristall gebildet wird, oder das hexagonale Gitter, das von Bienen in einem Bienenstock gebildet wird .“ Andere berühmte Probleme der Graphentheorie sind das Finden eines Weges, um aus einem Labyrinth oder Labyrinth zu entkommen, oder das Finden der Reihenfolge der Züge mit einem Ritter auf einem Schachbrett, so dass jedes Feld nur einmal gelandet ist und der Ritter zu dem Raum zurückkehrt, auf dem er gelandet ist . Einige andere Probleme der Graphentheorie sind seit Jahrhunderten ungelöst .

Das Schicksal von Königsberg

Während die Graphentheorie boomte, nachdem Euler das Königsberger Brückenproblem gelöst hatte, hatte die Stadt Königsberg ein ganz anderes Schicksal. 1875 beschlossen die Königsberger, eine neue Brücke zwischen den Knoten B und C zu bauen und die Anzahl der Verbindungen dieser beiden Landmassen auf vier zu erhöhen. Dies bedeutete, dass nur zwei Landmassen eine ungerade Anzahl von Verbindungen hatten, was eine ziemlich einfache Lösung für das Problem darstellte. Die Schaffung der zusätzlichen Brücke kann unbewusst durch den Wunsch nach einem Weg zur Lösung des berühmten Problems der Stadt verursacht worden sein. Eine neue Brücke löste jedoch nicht alle zukünftigen Probleme Königsbergs, da die Stadt im neunzehnten Jahrhundert nicht erwartet hatte, „das traurige und vom Krieg zerrissene Schicksal, das sie als Gastgeber einer der heftigsten Schlachten des Zweiten Weltkriegs erwartete.“ Während vier Tagen im August 1944 zerstörten britische Bomber sowohl die Altstadt als auch den nördlichen Teil Königsbergs. Im Januar und Februar 1945 wird die Region um Königsberg von russischen Streitkräften umzingelt. Deutsche Zivilisten beginnen aus der Stadt zu evakuieren, bewegen sich aber zu spät. Tausende Menschen werden bei dem Versuch getötet, mit dem Boot und zu Fuß über das eisige Wasser des Kurischen Haffs zu fliehen. Im April 1945 erobert die Rote Armee Königsberg, etwa neunzig Prozent der Altstadt liegen in Trümmern.

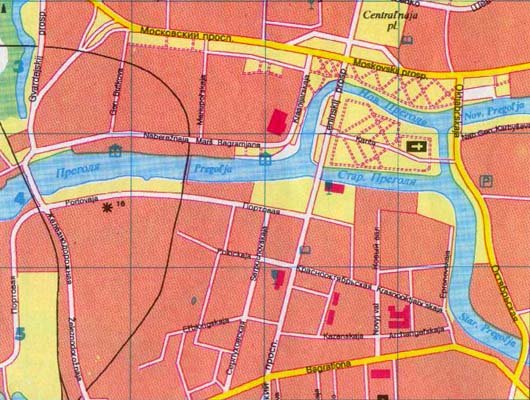
Eine aktuelle Straßenkarte von Königsberg finden Sie unten . Diese Karte zeigt, wie sehr sich die Stadt verändert hat. Viele der Brücken wurden während der Bombenanschläge zerstört, und die Stadt kann nicht mehr die gleiche faszinierende Frage stellen, die sie im achtzehnten Jahrhundert stellen konnte. Zusammen mit einem stark veränderten Layout, Die Stadt Königsberg hat einen neuen Namen, Kaliningrad, mit dem Fluss Pregel umbenannt Pregolya . Während das Schicksal Königsbergs schrecklich ist, führte das alte Kaffeehausproblem der Bürger, jede ihrer alten sieben Brücken genau einmal zu überqueren, zur Bildung eines völlig neuen Zweigs der Mathematik, der Graphentheorie.

Biggs, Norman L., E. K. Lloyd und Robin J. Wilson. Graphentheorie: 1736-1936. Oxford: Clarendon Press, 1976.

Das Leben ist schön. Euler: Der Meister von uns allen. Washington: Die mathematische Vereinigung von Amerika, 1999.Euler, Leonhard, ‚Solutio problematis ad geometriam situs pertinentis‘ (1741), Eneström 53, MAA Euler Archiv.

„Geschichte der Mathematik: Über Leonhard Euler (1707-1783).“ Wissenschaftswoche (2003). 6. November. 2005.

Hopkins, Brian und Robin Wilson. „Die Wahrheit über Königsberg.“ College Mathematics Journal (2004), 35, 198-207.

„Königsberger Brücken.“ Die MacTutor Geschichte der Mathematik Archiv:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Anmerkung des Herausgebers: Dieser Artikel wurde ursprünglich in Convergence, Volume 3 (2006) veröffentlicht.