Der Vier-Farben-Satz
Die Vier-Farben-Vermutung wurde erstmals vor etwas mehr als 150 Jahren aufgestellt und 1976 endgültig bewiesen. Es ist ein herausragendes Beispiel dafür, wie alte Ideen mit neuen Entdeckungen und Techniken in verschiedenen Bereichen der Mathematik kombiniert werden, um neue Ansätze für ein Problem zu bieten. Es ist auch ein Beispiel dafür, wie ein scheinbar einfaches Problem gedacht wurde, um ‚gelöst‘ zu werden, aber dann komplexer wurde, und es ist das erste spektakuläre Beispiel, bei dem ein Computer an der Beweisführung eines mathematischen Satzes beteiligt war.
Am Anfang
Die Vermutung, dass jede Karte mit nur vier Farben eingefärbt werden könnte, erschien erstmals 1852 in einem Brief von August De Morgan (1806-1871), erster Professor für Mathematik am New University College London, an seinen Freund William RowanHamilton (1805-1865), den berühmten irischen Mathematiker. Es hadbeen vorgeschlagen, De Morgan von einem seiner Studenten, FrederikGuthrie, im Namen seines älteren Bruders Francis (der später becameprofessor für Mathematik an der Universität von Kapstadt).


Augustus De Morgan (1807-1871) undWilliam Rowan Hamilton (1805-1865)
Das Problem, so einfach beschrieben, aber so tantalizingly difficultto beweisen, fing die Phantasie vieler Mathematiker an derzeit. In den späten 1860er Jahren nahm De Morgan das Problem und seine Forschung sogar mit nach Amerika, wo sich unter anderem Benjamin Peirce (1809-1880), ein berühmter Mathematiker und Astronom, dafür interessierte, um seine logischen Methoden zu entwickeln.
De Morgan nutzte die Tatsache, dass in einer Karte mit vier Regionen, die jeweils die anderen drei berühren, eine von ihnen vollständig von der anderen umschlossen ist. Da er keinen Weg finden konnte, dies zu beweisen, benutzte er es als Axiom , die Grundlage seines Beweises.
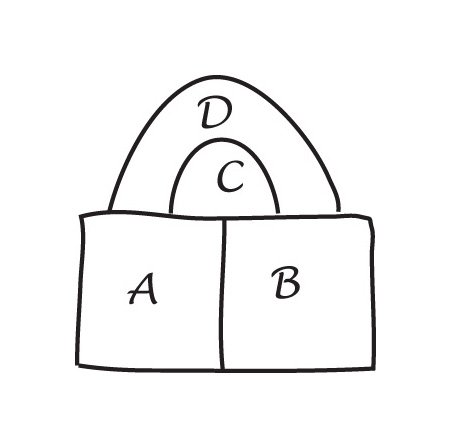
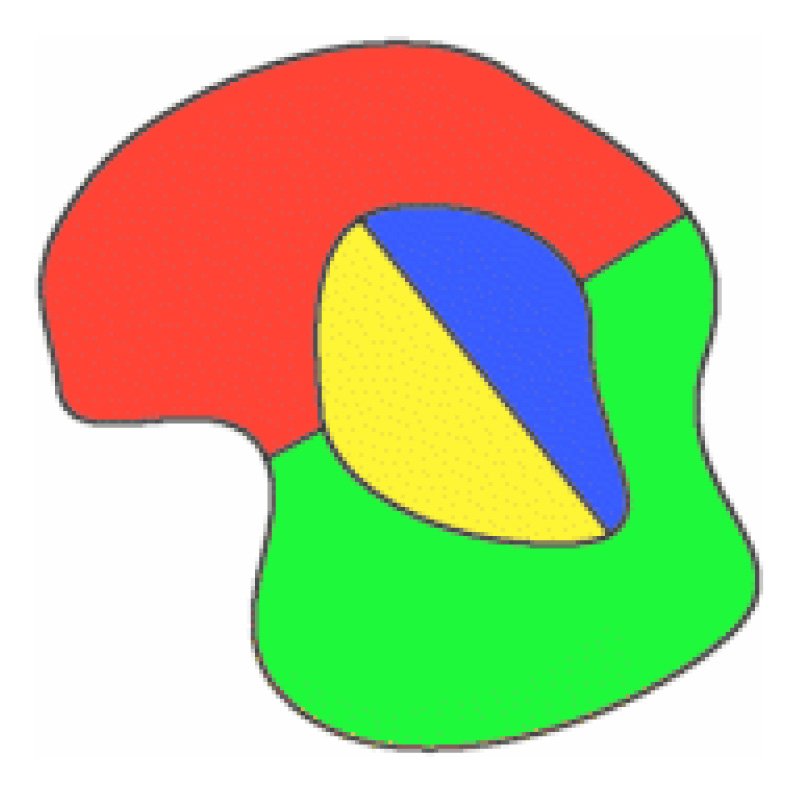
Eine Kopie von De Morgans Originalsketch in seinem Brief an Hamilton und eine einfache Vierfarbkarte.
1878 fragte Arthur Cayley (1821-1895) bei einem Treffen der Londoner Mathematischen Gesellschaft, ob jemand eine Lösung für De Morgans ursprüngliche Frage gefunden habe, aber obwohl es ein gewisses Interesse gegeben habe, habe niemand nennenswerte Fortschritte gemacht. Cayley interessierte sich für das Problem und veröffentlichte 1879 ein kurzes Papier über die Färbung von Karten, in dem er einige der Schwierigkeiten beim Versuch eines Beweises erklärte und einige wichtige Beiträge zur Lösung des Problems leistete. Seine Frage, dass, ‚Wenn eine bestimmte Karte alreadysuccessfully mit vier Farben gefärbt ist, und wir einen anderen Bereich hinzufügen, können wir immer noch die gleiche Färbung halten?‘ begann eine andere Linie ofenquiry, die zur Anwendung von mathematicalinduction auf das Problem geführt.

Arthur Cayley (1821-1895)
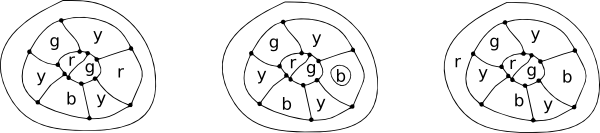
Arthur Cayley zeigte, dass es nicht immer möglich war, die ursprüngliche Farbe beizubehalten, wenn bereits vier Farben zum Einfärben einer Karte verwendet wurden und eine neue Region hinzugefügt wurde.
Oben wurden alle vier Farben auf der Originalkarte verwendet, und eine Region wird gezeichnet, um sie zu umgeben. In diesem Fall wird ein roter Bereich in Blau geändert, sodass Rot für den neuen Umgebungsbereich verwendet werden kann.
Cayley stellte auch fest, dass es möglich war, eine Version des Problems zu lösen, indem die Art und Weise, wie sich die Grenzen trafen, eingeschränkt wurde. Zum Beispiel haben Karten, auf denen sich nur drei Länder trafen, drei Kanten, die sich auf der avertex treffen. Diese werden ‚kubische Karten‘ genannt, und die Karten, die in der folgenden Diskussion verwendet werden, sind alle kubische Karten. Auch, wenn eine karte kann becoloured mit vier farben, nur drei farben erscheinen auf theborder.
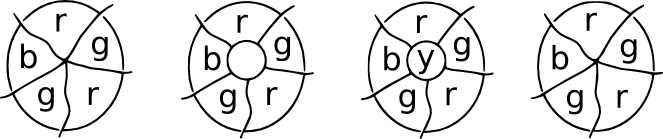
Die Patch-Demonstration. Stellen Sie sich vor, dass sich an einer Stelle in einer Karte eine Reihe von Ländern an einem Punkt treffen. Legen Sie nun einen Patch über den Treffpunkt, und alle neuen Treffpunkte haben drei Ränder, die von ihnen ausgehen. Dies sind kubische Karten,und eine vierte Farbe kann für die zentrale Region verwendet werden. Nach dem Entfernen des Patches können wir zur ursprünglichen Farbe zurückkehren.
Einige alte Techniken, neue Bedingungen und mehr Probleme!
Um die Entwicklung des Problems zu verfolgen, müssen wir kurz einige der Ideen, Verfahren und Techniken untersuchen, die Mathematiker bei ihren Lösungsversuchen entwickelt haben.
Die einzige Fünf-Nachbarn-Vermutung
‚Wenn Sie ein bestimmtes Problem nicht lösen können, finden Sie ein einfacheres, das Sie lösen können.(Polya. Wie man es löst)
‚Jede Karte hat mindestens ein Land mit fünf oder weniger Nachbarn.‘
Stellen Sie sich eine Karte einer Insel vor, die vom Meer umgeben ist. In thecolouring der Länder der Insel, zählen wir das Meer als oneregion. Einige Länder haben möglicherweise nur zwei Grenzen (ein Digon), etwadrei (wie in einem Dreieck), einige vier (ein Quadrat) und einige fünf (Apentagon) oder mehr.
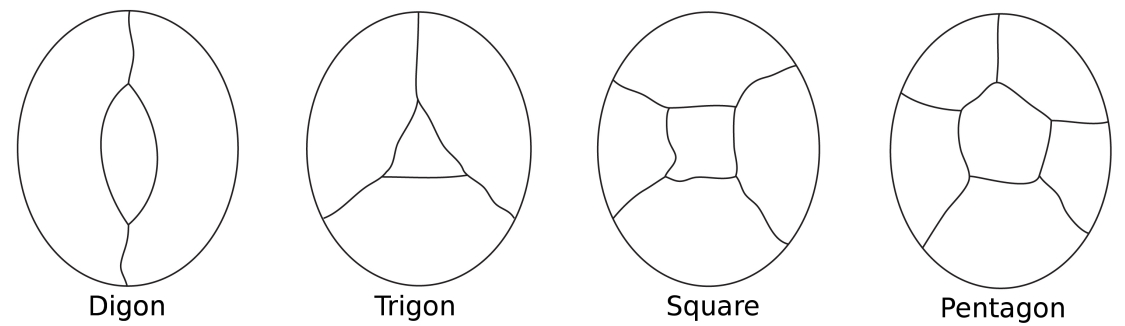
Die einfachstmöglichen Konfigurationen für die Umgebung einer zentralen Region.
Beachten Sie, dass in all diesen Konfigurationen jeder Knoten nur drei hatspitzen.
1813 wurde Eulers Formel für Polyeder von Augustin Cauchy (1759-1857) für zwei Dimensionen angepasst, indem das Polyeder auf eine Ebene projiziert wurde, wodurch das Netz des Festkörpers gebildet wurde. Auf diese Weise wurde die Formel $ f + v – e = 1 $, weilcauchy hat die ‚äußere‘ Region des Netzes nicht gezählt.

Augustin Cauchy (1759-1857)
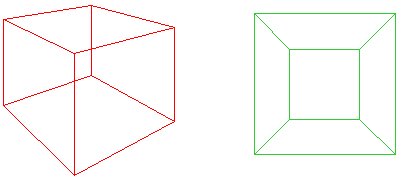
Stellen Sie sich vor, Sie zerquetschen den roten Würfel in einer Ebene, so dass seine Basis geöffnet wird, um den äußeren Rand des grünen Netzes zu bilden. Cauchys Idee war, eine Seite des Würfels auszuschneiden, so dass für ein ebenes Polygon $ f + v – e = 1 $. Alternativ, wenn die ‚Außenseite‘ des Netzes als ein Gesicht mit infinitearea betrachtet wird, dann haben wir immer noch $f + v – e = 2$
Wir können davon ausgehen, dass mindestens drei Grenzlinien (Kanten)von jedem Treffpunkt (Eckpunkte) ausgehen.
Der Beweis, dass die Karte mindestens ein Land hat, das von fünf oder weniger Nachbarn umgeben ist, läuft auf Widerspruch hinaus. Wenn dies zu einer Absurdität führt, haben wir einen Beweis.
Setzen Sie nun diese Werte in Eulers Formel: $$ f + v – e = 2 $$ undwir haben $$ 1/3(e) + 2/3(e) – e$$, was Null ist!
Das ist die Absurdität, also war unsere ursprüngliche Annahme falsch.Das bedeutet, dass es mindestens ein Land mit fünf oder weniger Nachbarn geben muss!
Minimale Verbrecher!
Eine andere Möglichkeit, das Vierfarbenproblem anzugehen, besteht darin, anzunehmen, dass es falsch ist, und zu sehen, wohin dies führt. Angenommen, es gibt Karten, die fünf Farben oder mehr benötigen, und wir wählen die Karten mit der kleinstmöglichen Anzahl von Ländern aus. Diese Karten werden als minimale Gegenbeispiele oderminimale Kriminelle!
Das bedeutet also, dass eine minimale Karte nicht mit vier Farben eingefärbt werden kann, aber jede Karte mit weniger Ländern kann mit vier Farben eingefärbt werden. Wenn wir zeigen können, dass Minimalkriminelle nicht existieren können, dann könnten wir in der Lage sein, einige Fortschritte zu machen.
Zum Beispiel können wir zeigen, dass ein minimaler Verbrecher kein Digon enthalten kann.
Von der ursprünglichen Karte, nehmen Sie eine Grenze von der Digon weg, undwir bekommen eine neue Karte mit weniger Ländern. Diese Karte kann mit vier Farben (aus unserer Annahme) gefärbt werden. Wir färben dann diese neue Farbe (wir brauchen nur zwei Farben). Ersetzen Sie nun den Rand, den wir entfernt haben, und färben Sie die Karte neu. Wir haben drei Farben verwendet, und da es noch eine weitere Farbe gibt, zeigt dies, dass unsere Karte mit vier Farben eingefärbt werden kann. Dies widerspricht jedoch unserer Annahme,sodass ein minimaler Verbrecher dies nicht kannenthalten einen Digon.
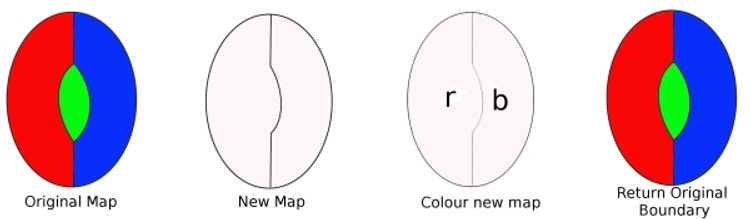
Um zu zeigen, dass ein Minimalkrimineller keine Region mit zwei Kanten (ein Digon) enthalten kann. Angenommen, es istein minimaler Verbrecher, der ein Digon enthält. Das Entfernen einer Kante bedeutet, dass die Karte weniger Regionen enthält. So kann diese neue Karte mit vier Farben eingefärbt werden. Ersetzen Sie nun die verlorene Kante. Da vorher nur zwei Farben benötigt wurden, bedeutet das Ersetzen der Kante, dass wir eine dritte Farbe verwenden können und immer noch eine vierte Farbe verwenden können. Ein Minimalkrimineller kann also mit vier Farben gefärbt werden. Daher kann ein Minimalcriminal kein Digon enthalten.
Dieses Verfahren kann wiederholt werden, um zu zeigen, dass ein minimaler Krimineller kein dreiseitiges Land (ein Trigon) enthalten kann, aber es bricht zusammen, wenn wir die Technik an einem Quadrat ausprobieren, denn wenn wir das Quadrat ersetzen, verwenden die Länder daneben möglicherweise alle vier Farben, sodass das Beweisverfahren fehlschlägt. Sobald dies geschehen ist, wird es offensichtlich, dass es nicht für Fünfecke und so weiter funktioniert.
Das Sechs-Farben-Theorem
Eine ähnliche Technik kann angewendet werden, um zu zeigen, dass das Sechs-Farben-Theorem wahr ist. Erstens gehen wir davon aus, dass es keine Karten gibt, die mit sechs Farben eingefärbt werden können. Einige der Karten können mit sieben Farben eingefärbt werden, also haben wir unser Ziel erreicht, wenn wir eine davon auswählen (eine minimale Anzahl), wenn wir zeigen können, dass es möglich ist, sie mit weniger als sieben Farben einzufärben.
Aus dem Beweis des Satzes der fünf Nachbarn ist es möglich, mit der Idee des minimalen Verbrechens fortzufahren, um zu zeigen, dass jede Karte mit sechs Farben gefärbt werden kann!
From Regions to Knots, Networks and Topology
Alfred Kempe (1849-1922)ging 1879 mit ähnlichen Techniken wie oben beschrieben von der Eigenschaft der fünf Nachbarn aus und entwickelte ein Verfahren, das als Methode der Kempe-Ketten bekannt ist, um einen Beweis für den Vierfarbensatz zu finden. Er veröffentlichte diesen Beweis indas American Journal of Mathematics. Er fand zwei einfachere Versionen, die im nächsten Jahr veröffentlicht wurden, und sein Beweis stand zehn Jahre, bevor Percy Heawood (1861-1955) zeigte, dass es einen wichtigen Fehler in der Proof-Methode gab, die Kempe verwendet hatte.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) und Percy Heawood (1861-1955)
1880 bot P.G. Tait (1831-1901), ein mathematischer Physiker, aneine Lösung für das Problem. Unabhängig davon hatte Tait festgestellt, dass Karten, bei denen sich an jedem Punkt eine gerade Anzahl von Grenzlinien trifft, mit zwei Farben eingefärbt werden können, obwohl dieses Ergebnis früher in Kempes Papieren aufgetaucht war.
Während 1876-77 wurde Tait bekannt für seine Studie undklassifizierung von Knoten. Zu dieser Zeit gab es eine Reihe vonverschiedene Theorien über die Struktur von Atomen. William Thompson(später Lord Kelvin 1824-1907), inspiriert von den Experimenten desdeutscher Physiker Hermann von Helmholtz (1821-1894) schlug die Theorie vor, dass Atome geknotete Röhren aus Äther seien. Kelvins Theorie der ‚Vortex-Atome‘ wurde etwa zwanzig Jahre lang ernst genommen und inspirierte Tait zu einer Klassifizierung von Knoten. Tait, Thomson und James Clark Maxwell (1831-1879) erfanden während ihres Studiums viele topologische Ideen. Kelvins Theorie war jedoch grundlegendfehlerhaft und Physiker verloren das Interesse an Taits Arbeit.


Hermann von Helmholtz (1821-1879), Lord Kelvin (1824-1907) und James Clark Maxwell (1831-1879)

Tait begann mit der Art und Weise, wie eine einzelne geschlossene Schnurschleife geknotet werden konnte. Er hatte zu Beginn keine systematische Methode und begann auf intuitive Weise, indem er eine einzige geschlossene Schleife nahm und mit der Art und Weise experimentierte, wie sie geknotet werden konnte. Natürlich musste die Schnur offen sein (wie ashoelace), dann geknotet und verbunden werden. Beachten Sie, dass sich die Über- Unter-Kreuzungen abwechseln, wenn Sie der Schnur um den Knoten folgen.Anschließend experimentierte er mit zwei Schlaufen und der Art und Weise, wie sie miteinander verknotet werden konnten. Hier sind Knoten mit bis zu sechs gezeigtkreuzungen für eine einzelne Schleife.
Eines der Ergebnisse von Taits Studie war seine Hamilton-Graph-Vermutung.
Eine Karte wird als Polyeder betrachtet, das auf einer Kugel gezeichnet ist, und kann dann auf eine Ebene projiziert werden. Tait schlug vor, dass jede kubische polyedrische Karte einen Hamilton-Zyklus hat . Taits Methode konzentrierte sich auf die Kanten des Graphen und zeigte, dass ein Hamiltonscher Zyklus eine vierfarbige Karte erzeugen konnte. Erst 1946 fand William Tutte (1917-2002) das erste Gegenbeispiel zu Taits Vermutung.
Tait und die Verbindung mit Knoten
Taitinitiierte 1880 das Studium der Snarks, als er bewies, dass der Vierfarbensatz der Aussage entsprach, dass kein Snark planar ist. Ein planarer Graph kann in der Ebene mit gezeichnet werdenkeine sich kreuzenden Kanten. Es sieht so aus, als ob Taits Idee von nicht-planaren Graphen aus seiner Untersuchung von Knoten und Hamilton-Pfaden stammen könnte .Der erste bekannte Snark war der Petersen-Graph, der 1898 entdeckt wurde, und Mathematiker begannen, nach mehr dieser Art von Graphen zu suchen, aber erst 1946 wurde ein weiterer Snark gefunden.
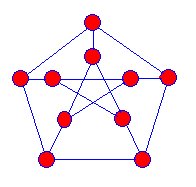 |
Snarks sind Projektionen von drei dimensional graphen auf theplane. Es gibt keine Eckpunkte, an denen sich die blauen Ränder zu kreuzen scheinen. Snarks haben folgende Eigenschaften:
|
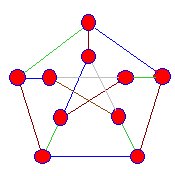 |
Die Kanten, die auf die Eckpunkte dieses Snarks treffen, sind blau, grün und braun gefärbt, aber wir erreichen immer ein Stadium, in dem dieser Prozess nicht fortgesetzt werden kann. |
Julius Peterson (1839-1910)
Die Jagd auf theSnark ist ein Gedicht von Lewis Carroll und Martin Gardnernannte diese Graphen Snarks, weil sie so schwer zu fassen waren.
Das Problem transformieren und neue Methoden finden.
Obwohl Heawood 1890 den Hauptfehler in Kempes Beweismethode fand, konnte er den Vierfarbensatz nicht weiter beweisen, aber er schaffte einen bedeutenden Durchbruch und bewies schlüssig, dass alle Karten mit fünf Farben gefärbt werden konnten.
Heawood leistete viele wichtige Beiträge zu diesem Problem und verlagerte den Fokus der Aufmerksamkeit von den Bereichen einer Karte auf die Grenzen zwischen ihnen. Bis 1898 hatte er bewiesen, dass, wenn die Anzahl der Kanten um jede Region durch 3 teilbar ist, die Regionen mit vier Farben gefärbt werden können.
Cauchys Beweis der Eulerschen Formel beinhaltete auch die Idee, dass jedes Netz eines Polyeders trianguliert werden kann, indem Kanten hinzugefügt werden, um nicht dreieckige Flächen zu Dreiecken zu machen. Er entwickelte dann ein Verfahren, bei dem er die Kanten nacheinander löschte, was zeigte, dass Eulers Formel bei jedem Schritt beibehalten werden konnte.
Cauchys Beweis der Eulerschen Formel
Cauchys 1813-Beweis der Eulerschen Formel begann mit der Idee einer Projektion eines Polyeders, um ein ebenes Netz zu erhalten. Des Weiteren demonstrierte er (a), dass jedes Netz trianguliert werden könne, und sein Beweis (b) der Eulerschen Formel wurde zu dieser Zeit akzeptiert.
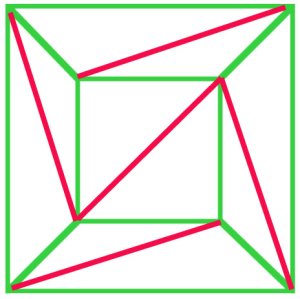 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
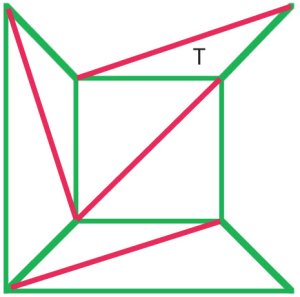 (b)
|
Cauchys Argument bestand darin, die Außenkanten nacheinander aus Diagramm(a) zu entfernen, und als er ein Stadium wie in Diagramm (b) erreichte, entfernte er das gesamte Dreieck T, wodurch Eulers Formel. Viele Mathematiker des frühen neunzehnten Jahrhunderts waren sich einig, dass dieses Verfahren einen Beweis für die Eulersche Formel für alle Polyeder darstellte. |
Um 1900 wussten Mathematiker, dass ein planarer Graph sein kannkonstruiert aus jeder Karte mit dem mächtigen Konzept der Dualität . Im Dual werden die Regionen durch Scheitelpunkte dargestellt, und zwei Scheitelpunkte werden durch eine Kante verbunden, wenn die Regionen benachbart sind. In diesen Graphen fragt die FourColour-Vermutung nun, ob die Eckpunkte des Graphen mit 4 Farben eingefärbt werden können, so dass keine zwei benachbarten Eckpunkte dieselbe Farbe haben.
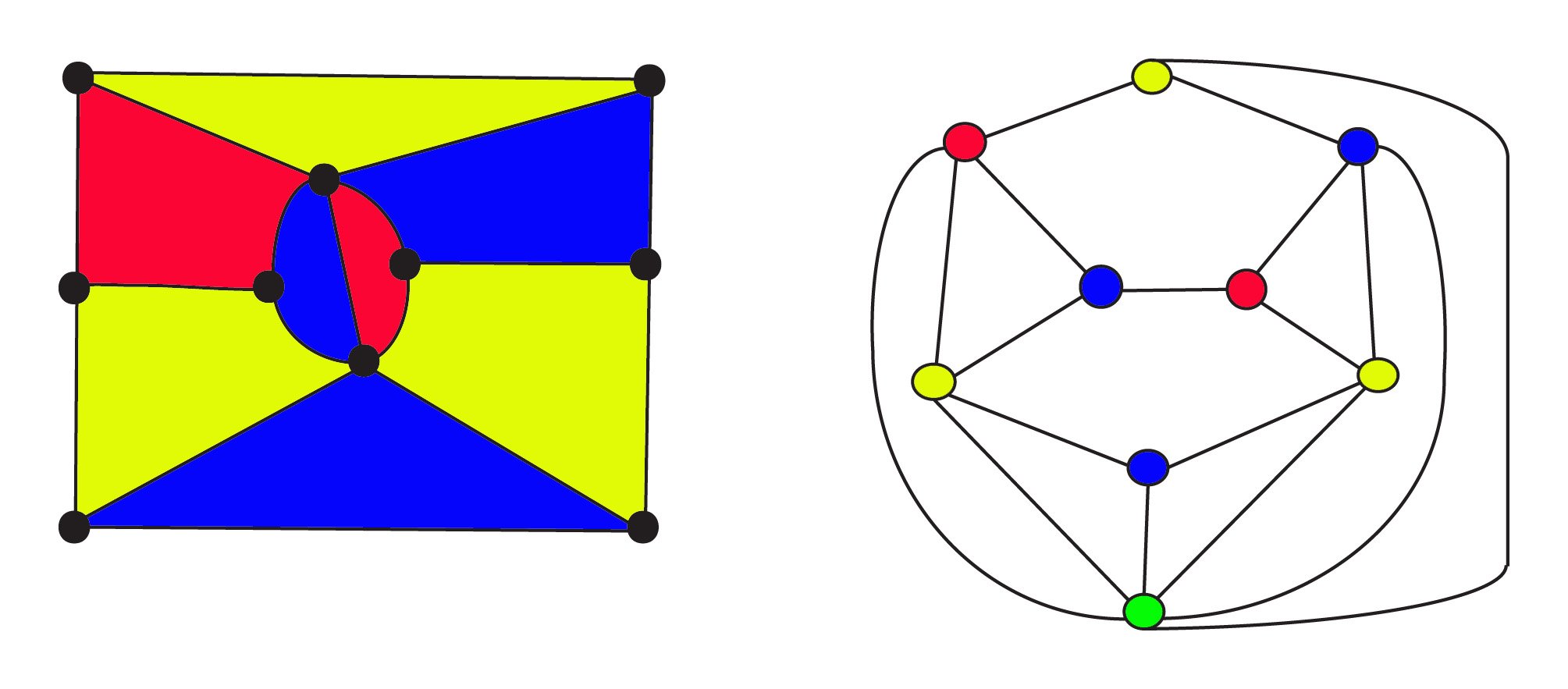
Die 3-farbige Karte auf der linken Seite hat$8$ Regionen $10$ Ecken und $17$ Kanten. Sein dualer Graph auf der rechten Seite hat $ 9 $ Regionen $ 9 $ Ecken und $ 17 $ Kanten, wobei die Ecken genauso gefärbt sind wie die Bereiche der Karte. Der greenvertex am unteren Rand des Diagramms stellt den unendlichen externalarea für die Karte dar. Sowohl die ursprüngliche Karte als auch ihr Dual gehorchen der Euler-Formel für Netzwerke $f + v – e = 1 $ oder $ \text{Regionen} +\text {Eckpunkte} – \ text {Kanten} = 1 $. Die Dualitätsbeziehung issymmetrisch: Das Dual des Dual wird der ursprüngliche Graph sein, woregionen und Eckpunkte werden ausgetauscht.
In der ersten Hälfte des zwanzigsten Jahrhunderts konzentrierten sich Mathematiker darauf, diese Art von Techniken zu modifizieren, umkomplizierte Karten auf spezielle Fälle zu reduzieren, die identifiziert und klassifiziert werden konnten, um ihre besonderen Eigenschaften zu untersuchen, und entwickelten die Idee eines minimalen Satzes von Kartenkonfigurationen, die getestet werden konnten.
In der ersten Instanz wurde angenommen, dass die Menge fast 9.000 Mitglieder enthielt, was eine enorme Aufgabe war, und so wandten sich die Mathematiker Computertechniken zu, um Algorithmen zu schreiben, die thetesting für sie tun konnten. Die Algorithmen verwendeten modifizierte Versionen von Kempes ursprünglicher Idee von Ketten zusammen mit anderen Techniken, um die Anzahl der Mitglieder der minimalen Menge zu reduzieren.Nachdem Kenneth App und Wolfgang Haken 1976 an der University of Illinois mit John Koch über das Problem der Reduzierbarkeit zusammengearbeitet hatten, reduzierten sie das Testproblem schließlich auf ein nicht vermeidbares Set mit 1.936 Konfigurationen, und es wurde eine vollständige Lösung für die Vier-Farben-Vermutung erreicht. Dieses Problem der Überprüfung der Reduzierbarkeit der Karten eins nach dem anderen wurde mit verschiedenen Programmen und verschiedenen Computern doppelt überprüft. Ihr Beweis zeigte, dass mindestens eine Karte mit der kleinstmöglichen Anzahl von Regionen, die fünf Farben erfordern, nicht existieren kann.
Seit dem ersten Beweis wurden effizientere Algorithmen für 4-Farbkarten gefunden, und bis 1994 war der unvermeidliche Satz von Konfigurationen auf 633 reduziert worden.
Ist ein ‚Proof‘ am Computer ein richtiger Beweis?
Da der Beweis mit Hilfe eines Computers erfolgte, gab es sofort einen Aufschrei. Viele Mathematiker und Philosophen behauptetendass der Beweis nicht legitim war. Einige sagten, dass Beweise nur von Menschen und nicht von Maschinen ‚bewiesen‘ werden sollten, während andere, die einen praktischeren Geist hatten, die Zuverlässigkeit sowohl der Algorithmen als auch der Fähigkeit der Maschinen, sie fehlerfrei auszuführen, in Frage stellten.Viele der von Mathematikern geschriebenen Beweise waren jedochfand sich als fehlerhaft, so dass das Argument über die Zuverlässigkeit leer erscheint.Unabhängig von den geäußerten Meinungen führte die Situation zu einer ernsthaften Diskussion über die Art des Beweises, die bis heute andauert.
Für pädagogische Notizen:
Verwenden Sie die Registerkarte Notizen oben in diesem Artikel oder klicken Sie hier .
Anmerkungen
- Weitere Einzelheiten zu diesem und den anderen Verfahren in diesem Abschnitt finden Sie in Robin Wilsons Buch Vier Farben genügen .
- Knoten können Linkshänder oder Rechtshänder sein, und heute gibt eswichtige Anwendungen dieser Eigenschaft in Chemie, Pharmazie,Biologie und Physik. (Siehe Pädagogische Hinweise)
- Benannt nach William Rowan Hamilton (1805-1865). Ein hamiltonscher Pfad in einem Diagramm besuchtjeder Scheitelpunkt genau einmal. Ein Hamiltonscher Zyklus (oder Kreislauf) ist ein Pfad, der jeden Scheitelpunkt genau einmal besucht und zum Startscheitelpunkt zurückkehrt.(Siehe Pädagogische Anmerkungen)
- Das Buch von Imre Lakatos, Beweise und Widerlegungen hat Adiskussion und Kritik an Cauchys Verfahren (Seiten 6 – 12), undviel mehr über die Geschichte von Eulers Satz.
- Die Idee der Dualität entstand im 16. und 17. Mathematiker wie Pascal und Desargues fanden heraus, dass neue Theoreme gefunden werden konnten, indem die Begriffe ‚Punkt‘ und ‚Linie‘ in Beschreibungen bestimmter geometrischer Konfigurationen ausgetauscht wurden. Ein Beispiel ist in regelmäßigen Polyedern, wo diescheitelpunkte eines entsprechen den Flächen des anderen. Also das Dualvon einem Tetraeder ist ein anderes Tetraeder, und das Dual eines Würfels istein Oktaeder. Das Dual des Dual ist das Originalpolyeder.
Das beste populäre, leicht zu lesende Buch über das Four ColourTheorem ist:
Wilson, R. (2003)
Four Colours Sufficient.In:London. Penguin Bücher.
Für eine detailliertere und technische Geschichte ist das Standardreferenzbuch:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Graphentheorie, 1736-1936
Oxford. In: Oxford University Press.
Dieser bringt uns auf den neuesten Stand, mit neueren Grundlagen und Philosophie.
Fritsch, R und Fritsch, G (2000)
Der Vierfarbensatz: Geschichte, topologische Grundlagen und Beweisidee
New York. In: Springer-Verlag.
Kaum ein allgemeines Geschichtsbuch enthält viel zu diesem Thema, aber das letzte Kapitel in Katz mit dem Titel ‚Computers and Applications‘ enthält einen Abschnitt zur Graphentheorie, und der Vierfarbensatz wird zweimal erwähnt.
Polya G. Wie man lösteses.
Dies ist das klassische Buch über Problemlösung. Es gab viele Ausgaben dieses Buches, seit es in den 1950er Jahren erschien, und es ist immer noch leicht verfügbar. Seltsamerweise wurden neuere Ausgaben mit dem Untertitel ‚A new aspect of Mathematical Method‘ versehen.
Lakatos, I. (1976) Beweise und Widerlegungen: Die Logik der mathematischen Entdeckung.In:Cambridge. C.U.P.
Dies ist ein weiteres wichtiges Buch, das in den 1970er Jahren zur Erforschung von Problemlösungen und Untersuchungen führte. Es beginnt als Klassenzimmer Diskussion zwischen einem Lehrer und einer Gruppe von studentsabout den Beweis der Euler-Formel, und reicht durch die Ideen, Einwände und Möglichkeiten, die tatsächlich Vonmathematiker und Wissenschaftler im neunzehnten Jahrhundert diskutiert wurden. Es wirft einige der wichtigsten Fragen zum Lehren und Lernenproblemlösen und zu mathematischen Methoden und Beweisen auf.
Verwandte Referenzen
Ich habe seit einiger Zeit ein kleines Buch über Streichspiele. Als ich in der Schule war, hieß es Cat’s Cradle, und wir spielten es in unserer Freizeit.
Vor kurzem hat eine französische Zeitschrift einen Artikel über die’Algebra‘ von String-Figuren veröffentlicht! Wenn Sie zu Amazon gehen, finden Sie ein interessantes Buch von Ann Swain und Michael Taylor mit dem Titel Finger Strings: A Book of Cats Cradles andString Figures, das im September 2008 von Floris Books veröffentlicht wird. Es gibt einige 80 Figuren mit farbigen beschrieben diagrams.It der spirale gebunden, so wird es offen bleiben, während sie folgen theinstructions. Es kommt auch mit ein paar String-Loops!
Für Knotenexperten ist das AshleyBook of Knots ein Klassiker für alle, die sich für Hunderte verschiedener Knotenarten und deren Verwendung interessieren. Amazon hatverschiedene Editionen zu unterschiedlichen Preisen erhältlich.
Web-Links
Für einen allgemeinen Überblick und Links zu vielen Personen und Themen, theMacTutor Website ist
Und natürlich MacTutor Biographien der beteiligten indeveloping all die verschiedenen mathematischen Aspekte können atthe MacTutor Biographien Index gefunden werden.
Der Vierfarbensatz und drei Beweise. Für die mathematicallypersistent die folgende Website hat einen faszinierenden neuen Ansatz toattacking das Problem der Konstruktion eines neuen Algorithmus für solvingthe Problem, und wie die Abhängigkeit von einem Computer zu reduzieren.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Für die Graphentheorie gibt Wikipedia einen guten Überblick, und Sie können das wirklich technische Zeug überspringen. Es zeigt die Arten von modernenanwendungen dieses Bereichs der Mathematik. Wenn Sie zu GraphColouring gehen und auf den Vierfarbensatz klicken, finden Sie viele weitere Informationen.
Eine interessante und nicht allzu technische Geschichte der Knotentheorie – wie eine Idee aus Kelvins Physik zur Atomtheorie zurückkehrtheute.
Der Verband der Mathematiklehrer hat Knotdesign-Poster erstellt. Gehen Sie zu ihrer Website und durchsuchen Sie die Alphabetischenliste der Ressourcen.
Erfahren Sie alles über Knoten im Knotenatlas! Wenn Sie kein Experte sind – genießen Sie einfach die Vielfalt und Komplexität der Datenbank „im Geiste des Wikis“
Künstlerischer und bunter – aber nicht weniger mathematisch ist die gesamte Plotseite.
Für diejenigen, die etwas von den ursprünglichen Sachen und historischen Details wollen, gehen Sie zur Geschichte der Knotentheorie auf: