9. Impedanz und Phasenwinkel
Nicht verpassen…
Untersuchen Sie Impedanz, Strom und Spannung in einer RLC-Schaltung im Applet später auf dieser Seite.
Impedanz
Die Impedanz einer Schaltung ist der gesamte effektive Widerstand gegen den Stromfluss durch eine Kombination der Elemente der Schaltung.
Symbol: Z
Einheiten: ‚Ω‘
Die Gesamtspannung über alle 3 Elemente (Widerstände, Kondensatoren und Induktivitäten) wird geschrieben
VRLC
Um diese Gesamtspannung zu finden, können wir nicht einfach die Spannungen VR, VL und VC addieren.
Da VL und VC als imaginäre Größen betrachtet werden, haben wir:
Impedanz VRLC = IZ
Also `Z = R + j(X_L− X_C)`
Nun ist die Größe (Größe oder absoluter Wert) von Z gegeben durch:
`|Z/=sqrt(R^2+(X_L-X_C)^2`
Phasenwinkel
`tan\ theta=(X_L-X_C)/R`
Winkel θ repräsentiert den Phasenwinkel zwischen dem Strom und der Spannung.
Vergleichen Sie dies mit dem Phasenwinkel, den wir zuvor in Graphen von y = a sin (bx + c) getroffen haben.
Beispiel 1
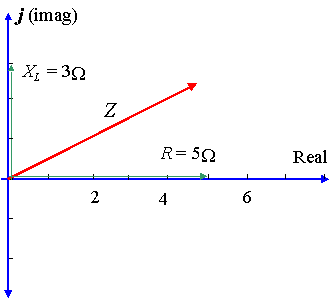
Eine Schaltung hat einen Widerstand von `5\ Ω` in Reihe mit einer Reaktanz über einer Induktivität von `3\ Ω`. Stellen Sie die Impedanz durch eine komplexe Zahl in polar dar.
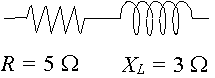
Antwort
In dieser fall, `X_L = 3\ Ω` und `X_C = 0` also `X_L- X_C= 3\ Ω`.
Also in rechteckiger Form wird die Impedanz geschrieben:
`Z = 5 + 3j\ Ω`
Mit dem Rechner wird die Größe von Z gegeben durch: `5.83`, und der Winkel `θ` (die Phasendifferenz) wird gegeben durch: `30.96^@`.
Die Spannung führt also den Strom um `30.96^@`, wie im Diagramm gezeigt.
Wenn wir Z als komplexe Zahl (in Polar-Form) darstellen, haben wir:
`Z = 5.83 ∠ 30.96^@\ Ω`.
Beispiel 2(a)
Ein bestimmter Wechselstromkreis hat einen Widerstand von `4\ Ω`, eine Reaktanz über einer Induktivität von `8\ Ω` und eine Reaktanz über einem Kondensator von `11\ Ω`. Drücken Sie die Impedanz der Schaltung als komplexe Zahl in polar aus.
Antwort
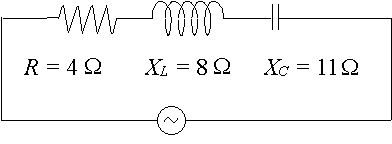
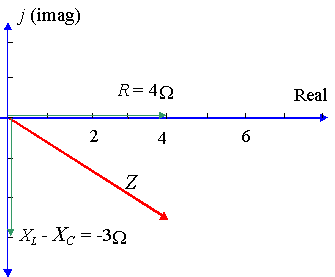
In diesem Fall haben wir: `X_L- X_C= 8 – 11 = -3\ Ω`
So ` Z = 4 – 3j\ Ω` in rechteckiger Form.
Um es nun in polar auszudrücken:
Mit dem Taschenrechner finden wir `r = 5` und ` θ = -36.87^@`.
Also `Z = 5 ∠ -36.87^@\ Ω`
Interaktives RLC-Diagramm
Unten finden Sie ein interaktives Diagramm zum Spielen (es ist kein statisches Bild). Sie können die Wirkung eines Widerstands, Kondensators und einer Induktivität auf die Gesamtimpedanz in einem Wechselstromkreis untersuchen.
Aktivitäten für dieses interaktive
- Spielen Sie zunächst einfach mit den Schiebereglern. Sie können:
Ziehen Sie den oberen Schieberegler nach links oder rechts, um die Impedanz aufgrund des Widerstands zu variieren, `R`,
Ziehen Sie den XL-Schieberegler nach oben oder unten, um die Impedanz aufgrund der Induktivität zu variieren, `X_L`, und
Ziehen Sie den XC-Schieberegler nach oben oder unten, um die Impedanz aufgrund des Kondensators zu variieren, `X_C`. - Beobachten Sie die Auswirkungen verschiedener Impedanzen auf die Werte von XL − XC und Z.
- Beobachten Sie die Auswirkungen verschiedener Impedanzen auf θ, den Winkel, den die rote „Ergebnis“ -Linie mit der Horizontalen einnimmt (im Bogenmaß).
- Betrachten Sie die Spannungs- und Stromdiagramme im Diagramm. Beobachten Sie die Verzögerung oder den Vorsprung, wenn Sie die Schieberegler ändern.
- Was haben Sie aus dem Spiel mit diesem interaktiven gelernt?