2.5: Darcys Gesetz – Strömung in einem porösen Medium
Darcys Gesetz ist entscheidend für das Verständnis vieler Zweige der Geologie, insbesondere der Hydrogeologie. Bevor wir uns das Gesetz ansehen und was es uns sagen kann, schauen wir uns an, wie es entwickelt wurde. Darcys Gesetz ist nach Henry Darcy benannt, einem französischen Ingenieur aus dem 19.Jahrhundert, der ein unterirdisches Druckrohrsystem zur Wasserversorgung der Stadt Dijon entwickelte. Das System, das auch die berühmten Dijon-Brunnen mit Wasser versorgte, revolutionierte die städtischen Wasser- und Abwassersysteme. Das System benötigte keine Pumpen und wurde rein durch die Schwerkraft angetrieben. Während des Entwicklungsprozesses des neuen Systems führte Darcy eine Reihe von Experimenten durch, bei denen er versuchte, Wasser ausschließlich mithilfe der Schwerkraft zu bewegen.
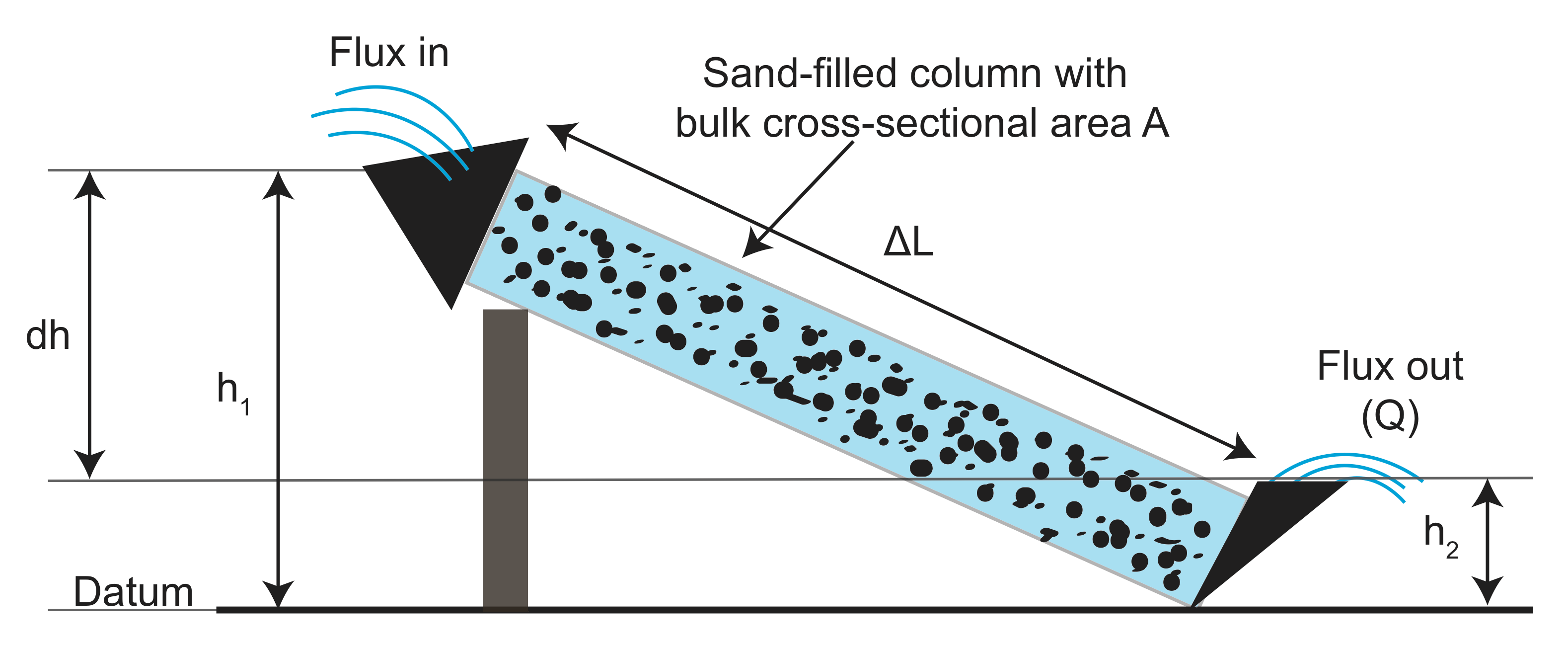
Aus den Experimenten, gesammelten Daten über die Länge der Rinne (\(L\)), die Querschnittsfläche der Rinne (\(A\)), der Höhenunterschied (\(h_1 – h_2\)) und der Fluss von Wasser, das aus \(Q\) sowohl mit als auch ohne körniges (Filter-) Material in der Rinne austritt. Anschließend zeichnete er die Flussmessung normiert durch die Fläche gegen das Verhältnis der Höhendifferenz zur Länge der Rinne (\( \frac{h_1 – h_2}{l}\)). Er fand heraus, dass es eine lineare Beziehung gibt und die Steigung von dem körnigen Material abhängt, das er in der Rinne verwendet hat:
\
was als Ableitung umgeschrieben werden kann,
\
wobei \(K\) die hydraulische Leitfähigkeit und \(\frac{dh}{dx}\) der hydraulische Gradient ist. \ (Q\), die Gesamtentladungsrate, hat Einheiten von \ (\frac {m ^ 3} {s} \), das Wasservolumen pro Zeit. Das negative Vorzeichen ist darauf zurückzuführen, dass das Fluid den hydraulischen Gradienten von höheren Werten zu niedrigeren Werten hinunterfließt (negativ).
Die hydraulische Leitfähigkeit ist ein physikalischer Parameter, der dafür verantwortlich ist, wie leicht sich das Fluid durch den Porenraum des Materials bewegen kann. In Darcys ursprünglichen Experimenten verwendete er Sande mit unterschiedlichen Korngrößen, jedoch kann die hydraulische Leitfähigkeit auch für feste Gesteine bestimmt werden, da die meisten Gesteine einen gewissen Porenraum haben.Im Anschluss an Darcys ursprüngliche Experimente wurden weitere Arbeiten durchgeführt, um die physikalischen Eigenschaften der Flüssigkeit und des Gesteins zu verstehen, die die effektive hydraulische Leitfähigkeit bestimmen. Aus diesen Experimenten wurde festgestellt, dass
\
wobei \(k\) die intrinsische Permeabilität des porösen Mediums (des Feststoffs), \ (\eta\) die dynamische Viskosität des Fluids und \(\ gamma = \rho g\) das spezifische Gewicht des Fluids ist, das von der Fluiddichte \ (\rho \) und der Schwerkraft \ (g \) abhängt.
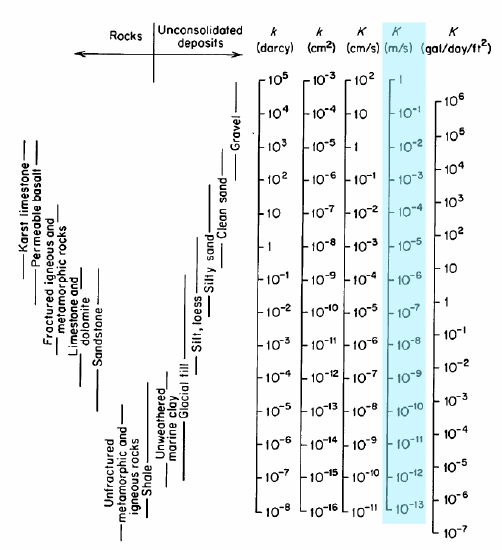
Die hervorgehobene Spalte in der Abbildung ist K, die hydraulische Leitfähigkeit in \(\frac{m}{s}\); Dies sind die Einheiten, die wir verwenden werden. Die hydraulische Leitfähigkeit wird manchmal auch als intrinsische Permeabilität \ (k\) mit Einheiten von darcys oder cm2 angegeben. Der gesamte Wertebereich für die hydraulische Leitfähigkeit beträgt 1-10-13 \ (\frac{m}{s}\). Experimente wie Darcys werden verwendet, um K in realen Materialien zu messen.
Die Entladungsrate \(Q\) ist ein Volumen flux (\ (m ^ 3 / s \)), aber wir denken normalerweise an Fluidfluss in Bezug auf eine Geschwindigkeit oder Geschwindigkeit. Die Entladungsfläche kann neu angeordnet werden, indem durch die Fläche dividiert wird, um den Darcy-Fluss zu definieren
\ \]
Oder in Bezug auf die intrinsische Permeabilität und den Druckgradienten,
\
wobei \(\eta\) die Flüssigkeitsviskosität ist (siehe unten für die Ableitung der zweiten Gleichung).
Es ist wichtig zu beachten, dass der Darcy-Fluss nicht der Flüssigkeitsgeschwindigkeit entspricht, obwohl er in Geschwindigkeitseinheiten angegeben ist. Die Fluidgeschwindigkeit wird durch die durchschnittliche lineare Geschwindigkeit (\(v_a\)) ermittelt, die der Durchschnitt der Geschwindigkeit aller möglichen Fluidwege durch die porösen Medien ist: das Finden dieses Werts liegt jedoch außerhalb des Bereichs dieser Klasse. Stattdessen werden wir feststellen, dass die Fluidgeschwindigkeit
\
wobei \(\varphi\) die Porosität und v die Fluidgeschwindigkeit ist. Die Porosität \(\varphi\) wird berechnet als Verhältnis des Volumens des Hohlraums zum Gesamtvolumen eines Materials \(\varphi=\frac{V_{void}}{V_{tot}}\) und wird üblicherweise als Bruchteil zwischen 0 und 1 oder als Prozentsatz ausgedrückt. Beachten Sie, dass wenn \(\varphi\leq\)1 dann ist die Fluidgeschwindigkeit größer als der Darcy-Fluss.
Ein weiterer Begriff, der bei der Diskussion der Strömung durch Gesteine und nicht konsolidierte Materialien auftaucht, ist die Permeabilität. Während die Porosität der tatsächliche Anteil der Poren (Hohlräume) im Gestein ist, können diese Hohlräume unterschiedliche Formen und unterschiedliche Konnektivität haben, was sich darauf auswirkt, wie leicht sich eine Flüssigkeit durch den Porenraum bewegen kann. Die Permeabilität ist ein Maß für die Leichtigkeit, mit der Flüssigkeiten und Gase durch ein Gestein gelangen können. Je fester das Material ist, desto geringer ist seine Durchlässigkeit. So haben „lose“ Materialien wie Kies eine hohe Durchlässigkeit. Einige Gesteine können auch eine anisotrope Permeabilität aufweisen, was bedeutet, dass Flüssigkeiten leicht in eine Richtung fließen können, aber nicht in eine andere. Ein Beispiel für ein Gestein mit anisotroper Permeabilität ist ein Schiefer. Flüssigkeiten können sich leicht innerhalb einer Schicht des Schiefers bewegen, können sich jedoch nicht über Schichten hinweg bewegen.
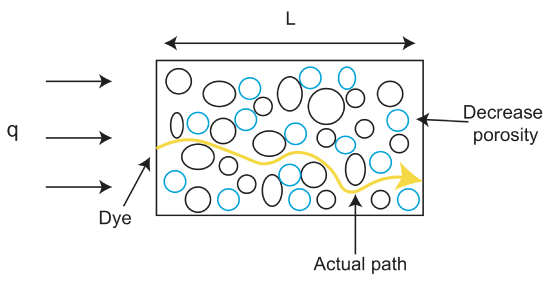
Fluidgeschwindigkeit
Lassen Sie uns ein grundlegendes Beispiel machen.
Wir erhalten \(q=2\frac{m}{min}\) und \(\varphi\) ist 25% und wollen die Fluidgeschwindigkeit finden.
Wir wandeln zuerst 25% in 0,25 um.
Dann \(v=\frac{2}{0.25}\frac{m}{min}\)
und
\(v=8 \frac{m}{min}\) ist die Fluidgeschwindigkeit.
Hydraulikkopf
Zurück zu Darcys Experimenten, was ist physikalischer Prozess treibt tatsächlich den Fluss der Flüssigkeit durch die Rinne?Der Begriff \(\frac{dh}{dx} \) wird als Hydraulikkopf bezeichnet, der der Flüssigkeitsdruck aufgrund des Gewichts eines Fluids relativ zu einem Referenzort ist: ein Druckgradient. Allerdings hat \(\frac {dh} {dx} \) keine Einheiten eines Drucks pro Längeneinheit, also warum heißt es der hydraulische Kopf?
Betrachten wir den Druck in der Rinne in Darcys Experimenten. Um die Experimente durchzuführen, hatte Darcy’s einen Wassertank am oberen Ende der Rinne, der einen konstanten Wasserstand am oberen Ende der Rinne bereitstellte, der der Höhe der Rinne \(h_1 \) . In ähnlicher Weise gab es unten einen Tank mit einem konstanten Wasserstand, der \(h_2\) entsprach. Daher ist der Flüssigkeitsdruck in jedem der Tanks aufgrund des Gewichts des Wassers durch \ (P = \ rho g h\) gegeben. Der Druckgradient zwischen der Oberseite und der Unterseite der Wolke wird dann
\
oder
\
Durch Darcys Gesetz ersetzt,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
Erinnern wir uns von oben, dass die hydraulische Leitfähigkeit in Bezug auf die intrinsische Permeabilität als \(K = k\frac{\gamma}{\eta}\) geschrieben werden kann, was äquivalent ist zu \(k\frac{\rho g}{\eta} \) oder Umlagerung, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Daher können wir ersetzen, um zwei äquivalente Ausdrücke für Darcys Gesetz zu geben, mit einem interms des Gradienten in der Höhe,
\
und der zweite in Bezug auf den Gradienten in Druck,
\
Somit wird \(\frac{dh}{dx}\) der hydraulische Kopf genannt, weil der physikalische Ursprung des Begriffs in Darcys Gesetz der Druckgradient in der Flüssigkeit ist, die den Fluss antreibt.
Wasser verlässt einen Aquifer
Lassen Sie uns nun ein Beispiel für die Berechnung der Flüssigkeitsgeschwindigkeit von Wasser durchführen, das in einen Aquifer eintritt. In der Skizze unten folgt die Grundwasserleiterhöhe der Topographie auf dem Hügel neben dem Tal mit dem Bach. Wasser fließt von Hochdruck (Kopfhöhe) in Richtung Tal und verlässt den Grundwasserleiter am Bach. Wir können Darcys Gesetz verwenden, um die Geschwindigkeit des Wasserflusses aus dem Grundwasserleiter abzuschätzen.
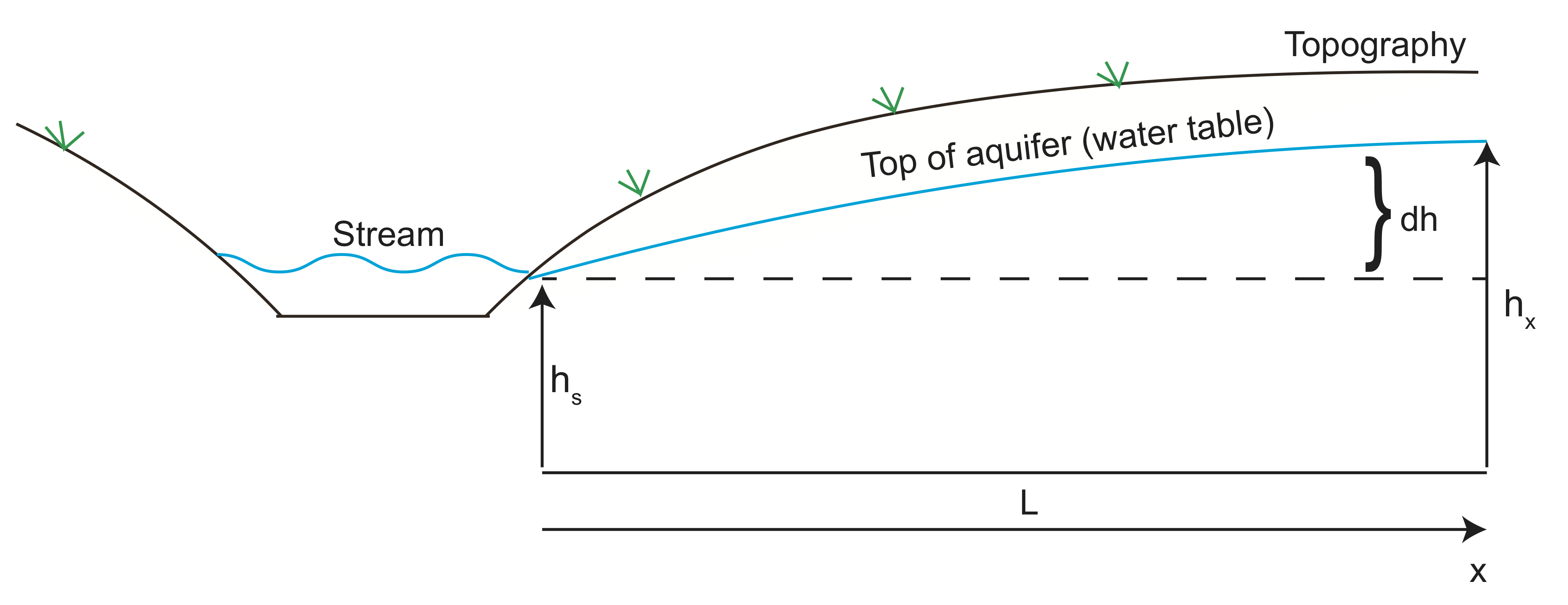
Unter Verwendung geophysikalischer Bildgebung wird die Höhe des Grundwasserleiters 10 m (\(dh\)) über der Bachhöhe von etwa 100 Metern (\(L\)) entfernt gefunden. Angenommen, die hydraulische Leitfähigkeit beträgt \ ( K = 10 ^ {-6} \) m / s und die Porosität beträgt \ (\ varphi = 30\)%.
Der Darcy-Fluss ist
\
\
\
Die Fluidgeschwindigkeit ist
\
\
\

Laminare versus turbulente Strömung
Eine der impliziten Annahmen in Darcys Gesetz ist, dass die Strömung laminar ist. Die laminare Strömung besteht aus dünnen Schichten oder Laminae von Flüssigkeit, die sich alle parallel zueinander bewegen. Im Gegensatz dazu ist die turbulente Strömung durch Wirbel, Wirbel und Wirbel gekennzeichnet, in denen benachbarte Flüssigkeitsschichten divergieren und unterschiedliche Wege stromabwärts nehmen.Eine Möglichkeit, wie wir quantifizieren können, ob ein Fluid laminar oder turbulent ist, besteht darin, die Reynoldsche Zahl für die Strömung zu berechnen, definiert als
\
Die Reynoldsche Zahl wird gefunden, indem die beiden Terme in der Impulsbilanz für die Strömung berücksichtigt werden. Der erste Term ist die Trägheitskraft pro Volumeneinheit, die die Strömung antreibt, \(\rho u\frac{du}{dx}\). Der zweite Term ist die viskose Kraft pro Volumeneinheit, die dem Fluss widersteht, \(\eta\ frac {d^ 2u} {dx ^ 2}\). Diese beiden Begriffe müssen ausgeglichen sein, damit wir sie gleich setzen können.
\
Als nächstes schreiben wir die Begriffe auf vereinfachte Weise neu, um nur die relevanten Dimensionen der Variablen zu erfassen. Um dies zu tun, gehen wir durch, was eine dimensionale Analyse genannt wird, in dem wir jede Variable ersetzen, mit einem Referenzwert, mal eine nicht-dimensionale Form der Variablen.
Zum Beispiel wird für den Term \(x\) nur \(L x’\) umgeschrieben, wobei \(L\) die Referenzlänge (die Flüssigkeitstiefe) und \(x’\) ist die nichtdimensionale Entfernung. In ähnlicher Weise lassen wir \(u = u_o u’\). Wenn wir diese in die Gleichung einsetzen, erhalten wir
\
Als nächstes kombinieren wir die konstanten Werte vorne
\
Beachten Sie, dass die Kombination der Variablen vorne die Reynoldsche Zahl ist
\
wobei die Variablen \ (u_o\) Strömungsgeschwindigkeit, L Flüssigkeitstiefe und die Variablen, die wir zuvor gesehen haben, \(\rho\) Flüssigkeitsdichte und \(\eta\) Flüssigkeitsviskosität sind. Durch diese Analyse stellen wir fest, dass jeder Fluss, der durch das Gleichgewicht dieser beiden Terme gekennzeichnet ist, verglichen werden kann, indem einfach der Wert der Reynolds-Zahl bekannt wird. Wenn beispielsweise eine Strömung eine Viskosität aufweist, die das 10-fache der Viskosität in einer anderen Strömung beträgt, verhalten sich die beiden Strömungen gleich, wenn die Dichte (oder Geschwindigkeit oder Länge) für den Fall mit höherer Viskosität ebenfalls um den Faktor 10 erhöht wird; das heißt, die Reynoldszahl für die beiden Strömungen ist gleich.
Um einen Darcy-Fluss zu haben, muss die Reynoldzahl kleiner als etwa 1-10 (laminar) sein. Für \(Re>1-10 \) ist die Strömung nicht streng laminar, aber noch nicht turbulent (nichtlinear, nicht laminar). Um eine turbulente Strömung zu haben, muss die Reynoldzahl größer als etwa 2000 sein.
Wenn Sie verstehen, dass die Konstanten im Zähler und im Nenner die Eigenschaften der Strömung in entgegengesetzter Weise beeinflussen, können Sie auch darüber nachdenken, wie sich verschiedene Flüssigkeiten unter ähnlichen äußeren Bedingungen verhalten. Zum Beispiel wird eine dichtere Flüssigkeit, die auch eine schnelle Geschwindigkeit hat, eine höhere Re haben und turbulentes Verhalten zeigen. Im Gegensatz dazu hat eine Flüssigkeit wie Eis, die eine hohe Viskosität hat und sich sehr langsam bewegt, eine niedrige Viskosität und wahrscheinlich eine laminare Strömung. Die hohe Viskosität des Eises stabilisiert die Strömung. Als weiteres Beispiel betrachten wir zwei Fluide, die sich beide mit der gleichen Geschwindigkeit bewegen und sich unterschiedlich verhalten, wenn die anderen Werte in der Reynoldschen Zahl \(\frac{\rho L}{\mu}\) unterschiedlich sind. Daher hängt die Strömungsart nicht nur von der Strömungsgeschwindigkeit ab, sondern auch von der Kombination von Variablen in der Reynoldschen Zahl.
Anwendung von Darcys Fluss
Darcys Gesetz ist die Hauptgleichung, die den Fluss in Grundwasserleitern und Brunnen regelt. Ohne sie wären wir nicht in der Lage, Brunnen zu bohren oder die Wasserbewegung in Grundwasserleitern zu verstehen, insbesondere im kalifornischen Central Valley, wo beide Ideen sowohl für die landwirtschaftliche Produktivität als auch für das Absinken des Grundwassers von entscheidender Bedeutung sind.
