Redaktørens Note

følgende studerendes forskningsrapport blev udarbejdet til Professor Judit Kardos’ Math 255-klasse, afholdt på College of ny trøje. Dette var et 3-kredit introduktionskursus i matematikens historie. Denne rapport blev talt til 30% af den endelige karakter. Det er et eksempel på den slags historiske forskning studerende kan gøre ved hjælp af sekundære kilder.

Leonard Eulers løsning på K-Kristnigsberg-problemet

K-Kristnigsberg

vores historie begynder i det 18.århundrede i den maleriske by K-Kristnigsberg, Preussen ved bredden af Pregelfloden. I 1254 grundlagde Teutoniske riddere byen K Kursnigsberg under ledelse af den bøhmiske Konge Ottoker II efter deres andet korstog mod preusserne. I middelalderen blev K Kurstnigsberg en meget vigtig by og handelscenter med sin placering strategisk placeret ved floden. Kunstværker fra det attende århundrede viser K. K. Som en blomstrende by, hvor flåder af skibe fylder Pregelen, og deres handel tilbyder en behagelig livsstil for både de lokale købmænd og deres familier. Den sunde Økonomi tillod byens folk at bygge syv broer over floden, hvoraf de fleste er forbundet med øen Kneiphof; deres placeringer kan ses på det ledsagende billede .

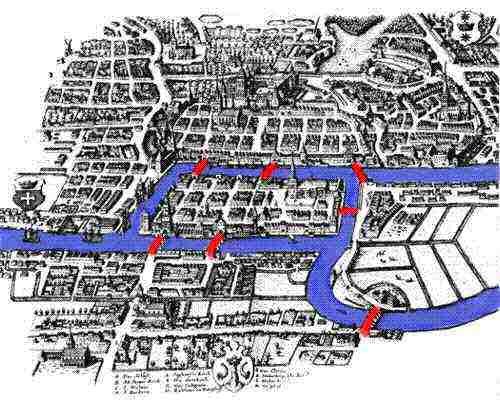
da floden flød rundt Kneiphof, der bogstaveligt betyder pub yard og en anden ø, delte den byen i fire forskellige regioner. De syv broer blev kaldt Blacksmith ‘s bridge, Connecting Bridge, Green Bridge, Merchant’ s Bridge, træbro, High Bridge og Honey Bridge. Ifølge lore plejede borgerne i K. K. Kursnigsberg at tilbringe søndag eftermiddag med at gå rundt i deres smukke by. Mens de gik, besluttede byens folk at skabe et spil for sig selv, hvor deres mål var at udtænke en måde, hvorpå de kunne gå rundt i byen og kun krydse hver af de syv broer en gang. Selvom ingen af borgerne i K. K. Kristnigsberg kunne opfinde en rute, der kun ville give dem mulighed for at krydse hver af broerne en gang, kunne de stadig ikke bevise, at det var umuligt. Heldig for dem var K Kursnigsberg ikke for langt fra St. Petersborg, hjemsted for den berømte matematiker Leonard Euler.

Euler og Broproblemet

hvorfor skulle Euler beskæftige sig med et problem, der ikke er relateret til matematikområdet? Hvorfor skulle sådan en stor matematiker tilbringe en stor del af tiden med et trivielt problem som K Kristnigsberg bro Problem? Euler var tydeligvis en travl mand, der udgav mere end 500 bøger og papirer i løbet af sin levetid. Alene i 1775 skrev han i gennemsnit et matematisk papir om ugen, og i løbet af sin levetid skrev han om en række emner udover matematik, herunder mekanik, optik, astronomi, navigation og hydrodynamik. Det er ikke overraskende, at Euler mente, at dette problem var trivielt og sagde i et brev fra 1736 til Carl Leonhard Gottlieb Ehler, borgmester i Dansigg, der bad ham om en løsning på problemet :

. . . Således ser du, mest ædle Sir, hvordan denne type løsning har ringe forhold til matematik, og jeg forstår ikke, hvorfor du forventer, at en matematiker producerer den snarere end nogen anden, for løsningen er baseret på fornuft alene, og dens opdagelse afhænger ikke af noget matematisk princip. På grund af dette ved jeg ikke, hvorfor selv spørgsmål, der har så lidt forhold til matematik, løses hurtigere af matematikere end af andre.

selvom Euler fandt problemet trivielt, var han stadig fascineret af det. I et brev skrevet samme år til Giovanni Marinoni, en italiensk matematiker og ingeniør, sagde Euler ,

dette spørgsmål er så banalt, men syntes mig værdig opmærksomhed i den geometri eller algebra eller endda kunsten at tælle var tilstrækkelig til at løse det.

Euler mente, at dette problem var relateret til et emne, som Gottfried engang havde diskuteret og længtes efter at arbejde med. Denne såkaldte positionsgeometri er det, der nu kaldes grafteori, som Euler introducerer og bruger, mens han løser dette berømte problem.

Eulers bevis

den 26.August 1735 præsenterer Euler et papir, der indeholder løsningen på Konigsberg-broproblemet. Han adresserer både dette specifikke problem såvel som en generel løsning med et hvilket som helst antal landmasser og et hvilket som helst antal broer. Dette papir, kaldet ‘Solutio problematis ad geometriam situs pertinentis’, blev senere offentliggjort i 1741 . Eulers papir er opdelt i enogtyve nummererede afsnit, og i det følgende vil en forenklet version af Eulers afsnit blive præsenteret.

i de to første afsnit i Eulers bevis introducerer han Konigsberg-Broproblemet. I punkt 1, Euler anfører, at han mener, at dette problem vedrører geometri, men ikke geometri velkendt af hans samtidige, der involverer målinger og beregninger, men i stedet en ny form for geometri, som Leibnis benævnt geometri Position. Derefter forklarer Euler i Afsnit 2 til sit publikum, hvordan Konigsberg-problemet fungerer. Euler leverede en skitse af problemet (se Eulers Figur 1) og kaldte de syv forskellige broer: A, b, c, d, e, f og g. i dette afsnit angiver han det generelle spørgsmål om problemet, “kan man finde ud af, om det er muligt at krydse hver bro nøjagtigt en gang?”

Eulers Figur 1 fra ‘Solutio problematis ad geometriam situs pertinentis,’ Enestr Prism 53

Efter at have angivet det generelle spørgsmål, han forsøger at løse, begynder Euler at udforske forskellige metoder til at finde en løsning. I Afsnit 3 fortæller Euler læseren, at han for at løse dette specifikke problem kunne nedskrive alle mulige stier, men denne teknik ville tage meget tid og ville ikke fungere for større konfigurationer med flere broer og landmasser. På grund af disse problemer besluttede Euler at vælge en anden metode til løsning af dette problem.

i Afsnit 4 begynder han at forenkle problemet ved at opfinde et praktisk system til at repræsentere krydsningen af en bro. Euler beslutter, at han i stedet for at bruge små bogstaver til at repræsentere krydsningen af en bro ville skrive de store bogstaver, der repræsenterer landmasserne. For eksempel, med henvisning til hans figur 1, AB ville betyde en rejse, der startede i landmasse A, og sluttede i B. Desuden, hvis nogen efter at have rejst fra landmasse A til B, nogen beslutter at flytte til landmasse D, Dette ville simpelthen betegnes, ABD. I Afsnit 5 fortsætter Euler sin diskussion om denne proces og forklarer, at selv om der er fire store bogstaver i ABDC, blev der kun krydset tre broer. Euler forklarer, at uanset hvor mange broer der er, vil der være endnu et brev til at repræsentere den nødvendige krydsning. På grund af dette krævede hele K-Kristnigsberg-Broproblemet syv broer, der skulle krydses, og derfor otte store bogstaver.

i Afsnit 6 fortsætter Euler med at forklare detaljerne i sin metode. Han fortæller læseren, at hvis der er mere end en bro, der kan krydses, når man går fra den ene landmasse til den anden, betyder det ikke noget, hvilken bro der bruges. For eksempel, selvom der er to broer, a og b, der kan tage en rejsende fra A til B, betyder det ikke noget med Eulers notation, hvilken bro der tages. I dette afsnit diskuterer Euler også det specifikke problem, han har at gøre med. Han forklarer ved hjælp af sin oprindelige figur, at k-Kristnigsberg-problemet har brug for nøjagtigt otte bogstaver, hvor parene (A,B) og (A,C) skal vises ved siden af hinanden nøjagtigt to gange, uanset hvilket bogstav der vises først. Derudover skal parene (A,D), (B,D) og (C, D) forekomme sammen nøjagtigt en gang for en sti,der krydser hver bro en gang og kun en gang for at eksistere.

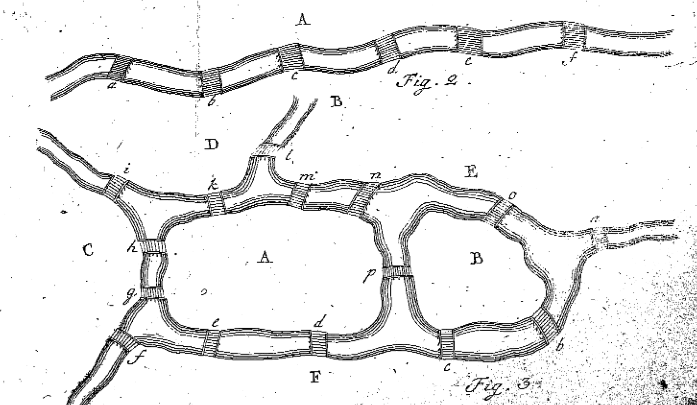
Eulers figur 2 og 3 fra ‘Solutio problematis ad geometriam situs pertinentis,’ Enestr Prism 53

i Afsnit 7 informerer Euler læseren om, at enten han har brug for at finde en sekvens på otte bogstaver, der tilfredsstiller problemet, eller han skal bevise, at der ikke findes en sådan sekvens. Før han gør dette for K-Kristnigsberg-Broproblemet, beslutter han at finde en regel for at finde ud af, om der findes en sti til et mere generelt problem. Han gør dette i Afsnit 8 ved at se på meget enklere eksempel på landmasser og broer. Euler tegner figur 2, Og han begynder at vurdere de situationer, hvor region A er rejst igennem. Euler siger, at hvis bro a rejses en gang, A var enten hvor rejsen begyndte eller sluttede, og blev derfor kun brugt en gang. Hvis broerne A, b og c alle køres en gang, bruges A nøjagtigt to gange, uanset om det er start-eller slutstedet. Tilsvarende, hvis fem broer fører til A, ville landmassen a forekomme nøjagtigt tre gange i rejsen. Euler siger, at “generelt, hvis antallet af broer er et ulige antal, og hvis det øges med en, er antallet af forekomster af A halvdelen af resultatet.”Med andre ord, hvis der er et ulige antal broer, der forbinder A til andre landmasser, skal du tilføje en til antallet af broer og dele den med to for at finde ud af, hvor mange samlede gange A skal bruges i stien, hvor hver bro bruges en gang og kun en gang (dvs. Samlede forekomster af A, hvor A har en ulige # af broer = (#af broer-1) / 2).

Ved hjælp af denne kendsgerning løser Euler k-Kristnigsberg-broproblemet i Afsnit 9. I så fald, da der er fem broer, der fører til en, det skal ske tre gange (se hans figur 1, ovenfor). Tilsvarende skal B, C og D vises to gange, da de alle har tre broer, der fører til dem. Derfor 3(for a) + 2(For B) + 2(For C) + 2(For D) = 9, Men Euler sagde allerede, at der kun må være otte forekomster for de syv broer. Dette er en modsigelse! Derfor er det umuligt at rejse broerne i byen K Kurstnigsberg en gang og kun en gang. Slutningen, eller er det? Mens befolkningen i K. K. K. kan være tilfreds med denne løsning, var den store matematiker Leonhard Euler ikke tilfreds. Euler fortsætter yderligere sit bevis for at håndtere mere generelle situationer.

Eulers generalisering

i Afsnit 10 fortsætter Euler sin diskussion med at bemærke, at hvis situationen involverer alle landmasser med et ulige antal broer, er det muligt at fortælle, om en rejse kun kan foretages ved hjælp af hver bro en gang. Euler siger, at hvis summen af antallet af gange, hvert bogstav skal vises, er en mere end det samlede antal broer, kan der foretages en rejse. Men hvis antallet af forekomster er større end en mere end antallet af broer, kan der ikke foretages en rejse, ligesom K-Kristnigsberg-Broproblemet. Dette skyldes, at reglen, som Euler giver for et ulige antal broer, ved hjælp af hans figur 2, gælder for den generelle situation, om der kun er en anden landmasse eller mere end en.

i Afsnit 11 og 12 omhandler Euler den situation, hvor en region har et lige antal broer knyttet til sig. Denne situation forekommer ikke i K-Kristnigsberg-problemet og er derfor blevet ignoreret indtil nu. I situationen med en landmasse med et lige antal broer kan der forekomme to tilfælde. Det første tilfælde er, når H er udgangspunktet for rejsen. I dette tilfælde vises H to gange, en gang som udgangspunkt og igen som slutpunkt. I det andet tilfælde er K ikke udgangspunktet. Hvis dette skulle ske, ville den kun vises en gang, da rejsen skulle komme ind gennem en bro og straks forlade gennem den eneste anden tilgængelige. På samme måde, hvis der er fire broer knyttet til H, afhænger antallet af forekomster af H af, om det er et udgangspunkt eller ej. Hvis rejsen starter i H, skal den vises tre gange, men hvis den ikke begynder i H, vises den kun to gange. Så generelt, hvis der er et lige antal broer fastgjort, så hvis rejsen ikke starter i H, vises h halvdelen af antallet af gange som broer (dvs. Forekomster af H, hvor H er lige og ikke udgangspunktet = (# af broer) / 2). Hvis rejsen starter i H vises halvdelen af antallet af gange som broer, plus en (dvs. forekomster af H hvor H er lige og udgangspunkt = ((#af broer) / 2) + 1).

i Afsnit 13 til 15 forklarer Euler, hvordan man finder ud af, om der findes en sti, der bruger hver bro en gang og kun en gang, og præsenterer sit eget eksempel for at vise, hvordan det fungerer. Euler forklarer først sin enkle seks-trins metode til at løse enhver generel situation med landmasser divideret med floder og forbundet med broer. Første Euler angiver hver landmasse med et stort bogstav. For det andet tager han det samlede antal broer, tilføjer en, og skriver dette over det Diagram, han er ved at lave. Dernæst tager han store bogstaver, sætter dem i en kolonne, og ved siden af dem skriver antallet af broer. For det fjerde angiver han med stjerner landmasserne, der har et lige antal broer. Derefter, ved siden af hvert lige antal, han skriver kr.af nummeret og ved siden af hvert ulige nummer placerer han kr. Endelig tilføjer Euler de tal, der er skrevet i kolonnen til højre, og hvis summen er en mindre end eller lig med antallet af broer plus en, er den krævede rejse mulig. Det er dog vigtigt at bemærke, at hvis summen er en mindre end antallet af broer plus en, skal rejsen starte fra en af landmasserne markeret med en stjerne. Hvis summen er lig med antallet af broer plus en, skal rejsen starte i et område, der ikke er markeret med en stjerne.

eksempler

brug af Konigsberg-problemet som hans første eksempel Euler viser følgende:

antal broer = 7, antal broer plus en = 8

Region broer gange Region skal vises

a 5 3

B 3 2

C 3 2

D 3 2

dog, 3 + 2 + 2 + 2 = 9, hvilket er mere end 8, så rejsen er umulig.

da dette eksempel er ret grundlæggende, beslutter Euler at designe sin egen situation med to øer, fire floder og femten broer. Situationen, som Euler skabte, kan ses i hans figur 3 ovenfor. Euler forsøger nu at finde ud af, om der er en sti, der gør det muligt for nogen at gå over hver bro en gang og kun en gang. Euler følger de samme trin som ovenfor og navngiver de fem forskellige regioner med store bogstaver og opretter en tabel for at kontrollere det, hvis det er muligt, som følgende:

antal broer = 15, antal broer plus en = 16

Region broer gange Region skal vises

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

f* 6 3

derudover, 4 + 2 + 2 + 2 + 3 + 3 = 16, hvilket svarer til antallet af broer plus en, hvilket betyder, at rejsen faktisk er mulig. Da summen er lig med antallet af broer plus en, skal rejsen starte i enten D eller E. Nu hvor Euler ved, at det er muligt at foretage en rejse, er alt, hvad han skal gøre, at angive, hvad stien vil være. Euler vælger stien EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, hvor han inkluderer hvilke broer der krydses mellem bogstaverne, der repræsenterer landmasserne. Selvom disse oplysninger er fremmede, da den nøjagtige bro ikke betyder noget ved at vide, at en rejse er mulig, er det nyttigt, når du vælger en sti. Dette er et godt eksempel, der viser den metode, som Euler ville bruge, når man løser ethvert problem af denne art.

Eulers konklusioner

i de næste par afsnit præsenterer Euler en anden måde at finde ud af, om en rejse kan foretages med et sæt landmasser, broer og floder. I betragtning 16 påpeger Euler, at det samlede antal numre, der er anført direkte til højre for landmasserne, udgør det dobbelte af det samlede antal broer. Denne kendsgerning bliver senere kendt som handshaking lemma. Dybest set siger håndtryk lemma, at hver bro tælles to gange, en gang for hver landmasse, som den er fastgjort til. I punkt 17 fortsætter Euler med at sige, at summen af alle broer, der fører til hver region, er jævn, da halvdelen af dette antal er lig med det samlede antal broer. Dette er dog umuligt, hvis der er et ulige antal landmasser med et ulige antal broer. Derfor beviser Euler, at hvis der er nogle ulige tal knyttet til landmasser, skal der være et lige antal af disse landmasser.

Dette er dog ikke nok til at bevise, når der er en sti, hvor hver bro bruges en gang og kun en gang, da K-Kristnigsberg-Broproblemet har et lige antal landmasser med et ulige antal broer, der går til dem. På grund af dette tilføjer Euler flere begrænsninger i Afsnit 18 og 19. Euler forklarer, at da det samlede antal broer, der er knyttet til hver landmasse, er lig med det dobbelte af antallet af broer (som det ses i handshaking lemma), så hvis du tilføjer to til dette beløb og derefter deler med to, får du antallet af samlede broer plus en. Dette tal er det samme som det, der blev brugt før, hvilket bruges til at fortælle, om en sti er mulig. Hvis alle tallene er lige, vil den tredje kolonne i tabellen summe til en mindre end det samlede antal broer plus en.

Euler forklarer derefter, at det er indlysende, at hvis der er to landmasser med et ulige antal broer, vil rejsen altid være mulig, hvis rejsen starter i en af regionerne med et ulige antal broer. Dette skyldes, at hvis de lige tal halveres, og hver af de ulige øges med en og halveres, vil summen af disse halvdele svare til en mere end det samlede antal broer. Men hvis der er fire eller flere landmasser med et ulige antal broer, så er det umuligt for der at være en sti. Dette skyldes, at summen af halvdelene af de ulige tal plus en sammen med summen af alle halvdelene af de lige tal vil gøre summen af den tredje kolonne større end det samlede antal broer plus en. Derfor beviste Euler netop, at der højst kan være to landmasser med et ulige antal broer.

Når dette er sagt, kan Euler nu drage sine konklusioner vedrørende mere generelle former for K-Kristnigsberg-Broproblemet. I Afsnit 20 giver Euler de tre retningslinjer, som nogen kan bruge til at finde ud af, om der findes en sti ved hjælp af hver bro en gang og kun en gang. For det første hævdede han, om der er mere end to landmasser med et ulige antal broer, så er en sådan rejse ikke mulig. For det andet, hvis antallet af broer er ulige for nøjagtigt to landmasser, så er rejsen mulig, hvis den starter i en af de to ulige nummererede landmasser. Endelig siger Euler, at hvis der ikke er regioner med et ulige antal landmasser, kan rejsen udføres fra en hvilken som helst region. Efter at have angivet disse tre fakta afslutter Euler sit bevis med Afsnit 21, der simpelthen siger, at efter at man har fundet ud af, at der findes en sti, skal de stadig gennemgå bestræbelserne på at skrive en sti, der fungerer. Euler mente, at metoden til at opnå dette var triviel, og han ønskede ikke at bruge meget tid på det. Imidlertid, Euler foreslog at koncentrere sig om, hvordan man kommer fra den ene landmasse til den anden, i stedet for først at koncentrere sig om de specifikke broer.

Eulers bevis og Grafteori

når man læser Eulers originale bevis, opdager man et relativt enkelt og let forståeligt matematikarbejde; det er dog ikke det egentlige bevis, men de mellemliggende trin, der gør dette problem berømt. Eulers store innovation var at se k-Kristnigsberg-broproblemet abstrakt ved at bruge linjer og bogstaver til at repræsentere den større situation med landmasser og broer. Han brugte store bogstaver til at repræsentere landmasser og små bogstaver til at repræsentere broer. Dette var en helt ny type tænkning for tiden, og i hans papir udløste Euler ved et uheld en ny gren af matematik kaldet grafteori, hvor en graf simpelthen er en samling af hjørner og kanter. I dag kaldes en sti i en graf, der indeholder hver kant af grafen en gang og kun en gang, en Eulerian sti på grund af dette problem. Fra det tidspunkt, hvor Euler løste dette problem til i dag, er grafteori blevet en vigtig gren af matematik, der styrer grundlaget for vores tænkning om netværk.

k-Kristnigsberg-Broproblemet er, hvorfor Biggs siger,

grafteoriens oprindelse er ydmyg, endda useriøs … de problemer, der førte til udviklingen af grafteori, var ofte lidt mere end gåder, designet til at teste opfindsomheden snarere end stimulere fantasien. Men på trods af den tilsyneladende trivialitet af sådanne gåder fangede de matematikernes interesse med det resultat, at grafteori er blevet et emne rig på teoretiske resultater af en overraskende variation og dybde.

som Biggs’ erklæring ville antyde, er dette problem så vigtigt, at det nævnes i det første kapitel i hver Grafteoribog, der blev gennemgået i biblioteket.efter Eulers opdagelse (eller opfindelse, afhængigt af hvordan læseren ser på det), grafteori boomede med store bidrag fra store matematikere som Augustin Cauchy, Vilhelm Hamilton, Arthur Cayley, Gustav Kirchhoff og George Polya. Disse mænd bidrog alle til at afdække “næsten alt, hvad der er kendt om store, men ordnede grafer, såsom gitteret dannet af atomer i en krystal eller det sekskantede gitter lavet af bier i en bikube .”Andre berømte grafteoriproblemer inkluderer at finde en måde at flygte fra en labyrint eller labyrint eller finde rækkefølgen af bevægelser med en ridder på et skakbræt, så hver firkant kun landes en gang, og ridderen vender tilbage til det rum, hvor han begyndte . Nogle andre grafteori problemer er gået uløst i århundreder .

K ‘s skæbne

mens grafteori boomede, efter at Euler løste K’ S problem med broen, havde byen K ‘ s skæbne en meget anden. I 1875 besluttede folket i K. K., at bygge en ny bro mellem knudepunkter B og C, hvilket øgede antallet af forbindelser mellem disse to landmasser til fire. Dette betød, at kun to landmasser havde et ulige antal links, hvilket gav en ret ligetil løsning på problemet. Oprettelsen af den ekstra bro kan eller måske ikke have været ubevidst forårsaget af ønsket om en sti til at løse byens berømte problem.

imidlertid løste en ny bro ikke alle K-Kristnigsbergs fremtidige problemer, som byen ikke forventede tilbage i det nittende århundrede, “den triste og krigsherjede skæbne, der ventede den som vært for en af de hårdeste slag i Anden Verdenskrig.”I løbet af fire dage i August 1944 ødelagde britiske bombefly både den gamle bydel og de nordlige dele af K. I januar og februar 1945 er regionen omkring K. kr.omgivet af russiske styrker. Tyske civile begynder at evakuere fra byen, men bevæger sig for sent. Tusinder af mennesker dræbes i forsøg på at flygte med båd og til Fods over det iskolde vand i den Curonian Lagoon. I April 1945 erobrede den Røde Hær K. K., hvor omkring halvfems procent af den gamle bydel lå i ruiner.

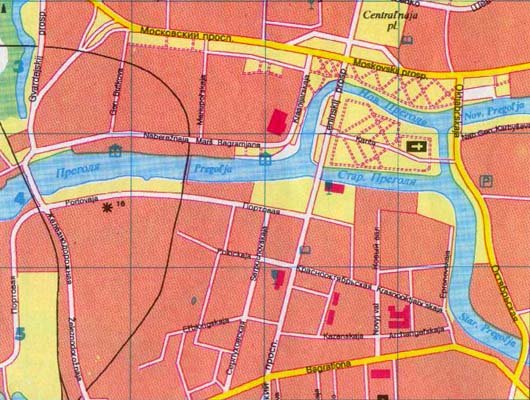
et aktuelt gadekort Over k Kristnigsberg er angivet nedenfor . Dette kort viser, hvor meget byen har ændret sig. Mange af broerne blev ødelagt under bombningerne, og byen kan ikke længere stille det samme spændende spørgsmål, de var i stand til i det attende århundrede. Sammen med et meget andet layout, byen K. K. har et nyt navn, Kaliningrad, med floden Pregel omdøbt til Pregolya . Mens K. K. ‘ s skæbne er forfærdelig, førte borgernes gamle kaffehusproblem med at krydse hver af deres gamle syv broer nøjagtigt en gang til dannelsen af en helt ny gren af matematik, grafteori.

Biggs, Norman L., E. K. Lloyd og Robin J. Grafteori: 1736-1936. Clarendon Press, 1976.

Dunham, Thomas. Euler: mesteren over os alle. Washington: Den matematiske sammenslutning af Amerika, 1999.

Euler, Leonhard, ‘løsning af problemer ad geometriam situs pertinentis’ (1741), Enestr kr.53, maa Euler arkiv.

” Matematikhistorie: på Leonhard Euler (1707-1783).”Videnskabsuge (2003). 6 Nov. 2005.Hopkins, Brian og Robin. “Sandheden om K Kurstnigsberg.”College Mathematics Journal (2004), 35, 198-207.

” Konigsberg broer.”MacTutor Historie Matematik arkiv:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Redaktørens note: Denne artikel blev oprindeligt offentliggjort i konvergens, bind 3 (2006).