i denne vejledning lærer vi om Hvedestenbro. Vi vil se Arbejdsprincippet for Hvedestenbro, få eksempler på kredsløb og nogle vigtige applikationer.

Introduktion til Hvedestenbro

i den virkelige verden støder vi på forskellige signaler, nogle af dem måles ved ændringer i modstand, og nogle af dem er med induktans og kapacitans.

Hvis vi overvejer modstanden, kan de fleste industrielle sensorer lide temperatur, belastning, Fugtighed, forskydning, væskeniveau osv. producerer ændringen i værdien af modstanden for en variabel ændring. Derfor er der behov for en signalkonditionering for hver modstandssensor.

generelt er modstandsmålingen opdelt i tre typer, måling af lav modstand, måling af medium modstand og måling af høj modstand. Hvis modstandsmålingen muligvis er fra et par milliohm til mikro ohm, betragtes det som en lav modstandsmåling.

denne måling bruges faktisk til forskningsformål. Hvis målingen er fra 1 ohm til 100 k kaldes generelt en medium modstandsmåling. Potentiometer, termistorer osv. målingen falder ind under denne kategori.

og meget høj modstandsmåling betragtes fra 100 kilo ohm til større end 100 mega ohm. For at finde modstandens middelværdi anvendes forskellige metoder, men for det meste anvendes Hvedestenbro.

Hvad er Bro?

det mest almindelige og enkleste bronetværk til at finde modstanden er DC-Hvedestenbroen. Denne bro bruges, hvor små ændringer i modstand skal måles som i sensorapplikationer. Dette bruges til at konvertere en modstandsændring til en spændingsændring af en transducer.

kombinationen af denne bro med operationsforstærker bruges i vid udstrækning i industrier til forskellige transducere og sensorer. En Hvedestenbro består af fire modstande, der er forbundet i form af en diamant med forsyningskilden og indikatorinstrumenter som vist i figur.

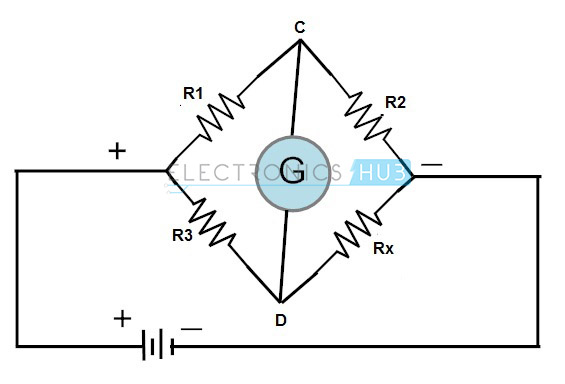
denne bro bruges til at finde den ukendte modstand meget præcist ved at sammenligne den med en kendt modstandsværdi. I denne bro bruges null eller afbalanceret tilstand til at finde modstanden.

for denne brobalancerede tilstandsspænding ved punkterne C og D skal være ens. Derfor strømmer ingen strøm gennem galvanometeret. For at få den afbalancerede tilstand skal en af modstandene være variabel.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This er betingelsen for at afbalancere broen. Og for at finde den ukendte værdi af modstand

rk = R3-L (R2/R1)

fra ovenstående ligning kan R4 eller rk beregnes ud fra den kendte værdi af modstand R3 og forholdet mellem R2 / R1. Derfor er de fleste tilfælde R2-og R1-værdier faste, og R3-værdien er variabel, så nulværdien opnås, og broen bliver afbalanceret.

arbejdsprincip

uden galvanometeret ser brokredsløbet bare ud som et spændingsdelerkredsløb som vist i nedenstående figur. Overvej R1= 20 ohm, R2= 40 ohm for den ene arm og for den anden overveje samme værdier af henholdsvis R3 og R4.

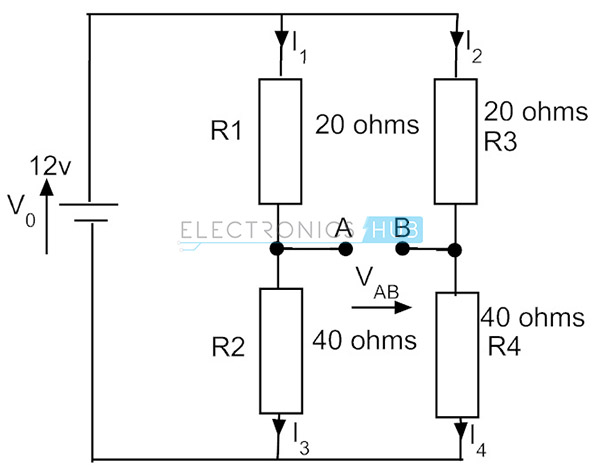
strømstrøm i første arm er

I1 = V/ (R1+R2)

I1 = 12V/ (20+40)

I1 = 0.2 a

og spænding ved punkt C er lig med spændingsfaldet ved modstand R2,

VR2 = i1 liter R2= 0.2 liter 40 = 8v

tilsvarende spændingen på tværs R1 er 4V (0,2 liter 20). På grund af de samme modstandsværdier vil spændinger ved R4 og R3 være de samme som henholdsvis R1 og R2. Derfor er spændingerne på punkterne A og B ens, derfor viser galvanometeret nulaflæsning, da den potentielle forskel er nul. I dette tilfælde siges broen at være i afbalanceret tilstand.

Antag, at hvis vi vender modstandene i den anden arm, er strømmen den samme på grund af seriekredsløbet. Men spændingen over modstanden R4 ændres, dvs. 0,2 * 20 = 4V. Så på denne betingelse spænding over punkterne A og B er forskellige og eksisterer en potentiel forskel på 8 – 4 = 4V. dette er broens ubalancerede tilstand.

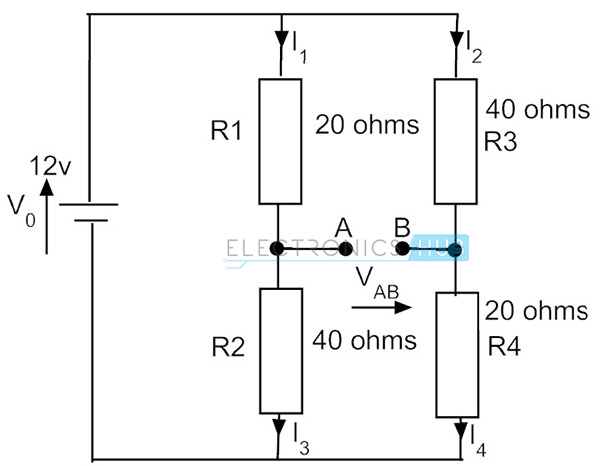
eksempel på Hvedestenbro

ovenfra er Hvedestenbroen ubalanceret, når voltmeteraflæsningen ikke er nul. Denne aflæsning kan være positiv eller negativ afhænger af størrelsen af spændingerne ved målerterminalerne. Lad os overveje nedenstående kredsløb af Hvedestenbro, der er forbundet for at finde den ukendte modstandsværdi ved brug af modstands årti boks for at få den variable modstand af R3.

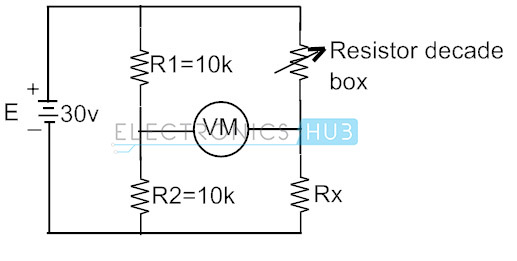
Vi ved, at betingelsen for brobalance er

R4 = R3 liter R2 / R1

103)/ (10 103)

rk=Rboks

Her i dette tilfælde afbalanceres hvedestenbroen ved at justere tiårets modstandsboks, indtil voltmeteret læser nulværdi. Og den tilsvarende modstandsværdi i kassen er lig med den ukendte modstand. Antag, at hvis spændingsnulbetingelsen forekommer ved 250 ohm i resistance decade-boksen, så er den ukendte modstand også 250 ohm.

Hvedestenbro til belastningsmåling

oftest til måling af stammen anvendes belastningsmålere, hvis elektriske modstand varierer med forholdsmæssig belastning i enheden. I praksis er spændingsmålerens modstandsområde fra 30 ohm til 3000 ohm. For en given stamme kan modstandsændringen kun være en brøkdel af fuld rækkevidde. For at måle ekstremt en brøkdel af modstandsændringer med høj nøjagtighed anvendes Hvedestenbrokonfiguration. Nedenstående figur viser Hvedestenbroen, hvor den ukendte modstand erstattes med en belastningsmåler.

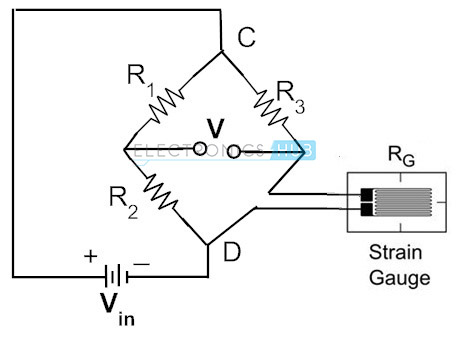
i ovenstående kredsløb er to modstande R1 og R2 lig med hinanden, og R3 er den variable modstand. Uden kraft påført belastningsmåleren varieres reostat og placeres til sidst således, at voltmeteret vil indikere nulafbøjning. Dette kaldes en brobalanceringstilstand. Denne betingelse repræsenterer, at der ikke er nogen belastning på måleren.

hvis belastningsmåleren enten er spændt eller komprimeret, kan modstanden øges eller formindskes. Derfor forårsager dette ubalance af broen. Dette giver en spændingsindikation på voltmeter svarer til belastningsændringen. Hvis belastningen på en belastningsmåler er mere, er spændingsforskellen på tværs af målerterminalerne mere. Hvis belastningen er nul, viser brobalancerne og måleren nulaflæsning.

dette handler om modstandsmåling ved hjælp af en Hvedestenbro til præcis måling. På grund af den fraktionerede måling af modstand anvendes Hvedestenbroer mest i belastningsmåler og termometermålinger.

applikationer

1. Hvedestenbroen bruges til at måle de meget lave modstandsværdier præcist.
2. Hvedestenbro sammen med operationsforstærker bruges til at måle de fysiske parametre som temperatur, belastning, lys osv.
3. Vi kan også måle mængderne kapacitans, induktans og impedans ved hjælp af variationerne på Hvedestenbroen.