Darcys lov er afgørende for at forstå mange grene af geologi, især hydrogeologi. Før vi ser på loven og hvad den kan fortælle os, lad os se på, hvordan den blev udviklet. Darcys lov er opkaldt efter Henry Darcy, en fransk ingeniør fra det 19.århundrede, der udviklede et underjordisk rørsystem under tryk for at levere vand rundt i byen Dijon. Systemet, der også leverede vand til de berømte Dijon-springvand, revolutionerede byens vand-og kloaksystemer. Systemet krævede ingen pumper og blev drevet udelukkende af tyngdekraften. Under udviklingen af det nye system gennemførte Darcy en række eksperimenter, hvor han forsøgte at flytte vand udelukkende ved hjælp af tyngdekraften.

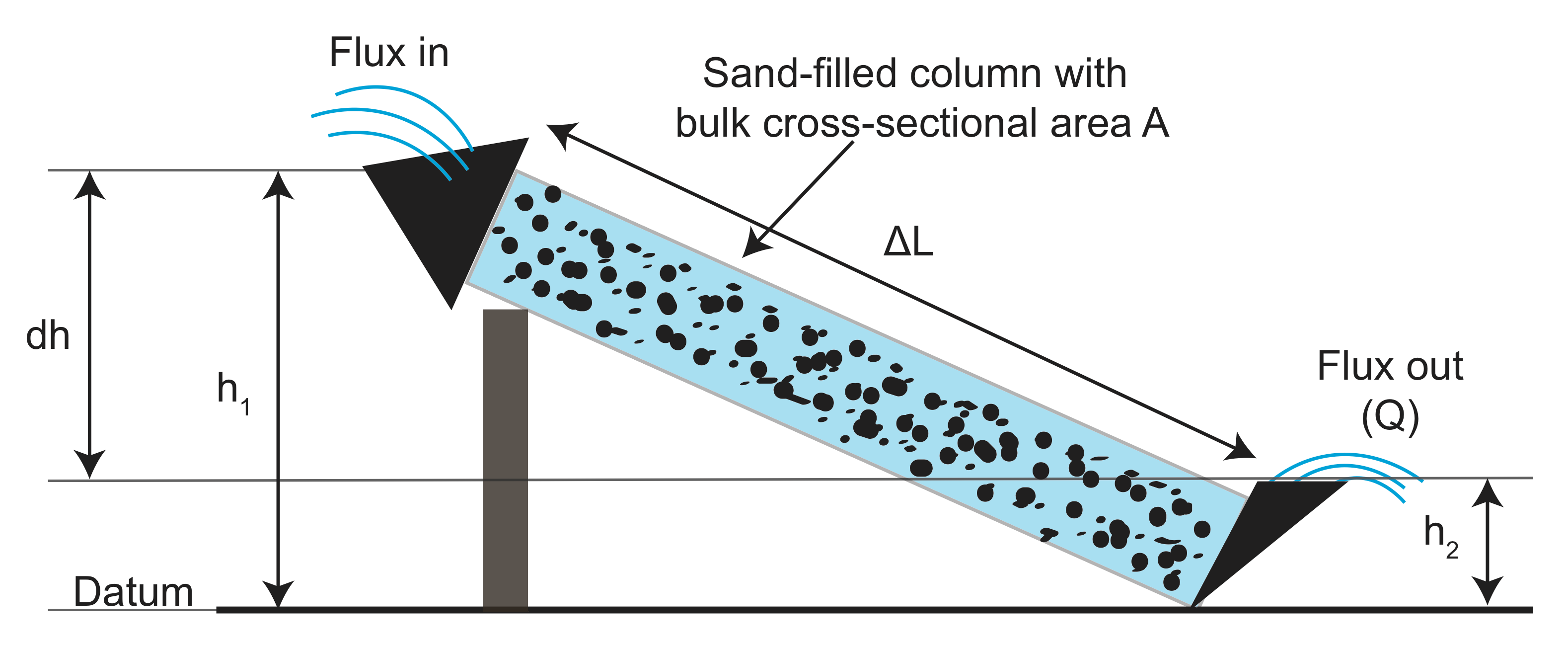
fra eksperimenterne indsamlede data om længden af flume (\(L\)), tværsnitsarealet af flume (\(a\)), højdeforskellen (\(h_1 – h_2\)) og strømmen af vand, der kommer ud \(K\) både med og uden granulært (filtrerende) materiale i Flume (\(a\)) Flume. Han plottede derefter fluksmålingen normaliseret af området versus forholdet mellem højdeforskellen og længden af flume (\( \frac{h_1 – h_2}{l}\)). Hvad han fandt er, at der er et lineært forhold, og hældningen afhænger af det granulære materiale, han brugte i flume:

\

som kan omskrives som et derivat,

\

hvor \(K\) er den hydrauliske ledningsevne og \(\frac{dh}{dh}\) er den hydrauliske gradient. \(K\), den samlede udledningshastighed, har enheder af \(\frac{m^3}{s}\), mængden af vand pr. Det negative tegn skyldes, at væsken strømmer ned (negativ) den hydrauliske gradient fra højere værdier til lavere værdier.

den hydrauliske ledningsevne er en fysisk parameter, der tegner sig for, hvor let væsken kan bevæge sig gennem porepladsen for materialet. I Darcy ‘ s originale eksperimenter brugte han sand med forskellige kornstørrelser, men den hydrauliske ledningsevne kan også bestemmes for faste klipper, da de fleste klipper har noget porerum.

efter Darcy ‘ s originale eksperimenter blev der udført yderligere arbejde for at forstå de fysiske egenskaber af væsken og Klippen, der bestemmer den effektive hydrauliske ledningsevne. Fra disse eksperimenter blev det fundet, at

\

hvor \(k\) er den indre permeabilitet af det porøse medium (det faste stof), \(\ETA\) er væskens dynamiske viskositet, og \(\gamma = \rho g\) er væskens specifikke vægt, som afhænger af væsketætheden, \(\rho\) og tyngdekraften, \(g\).

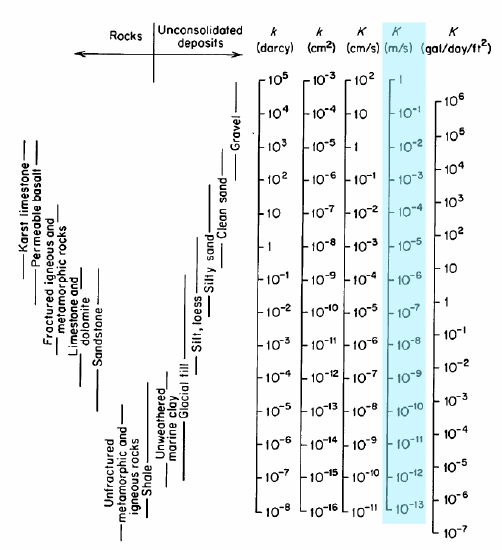
den fremhævede kolonne i figuren er K, den hydrauliske ledningsevne i \(\frac{m}{s}\); Dette er de enheder, vi vil bruge. Den hydrauliske ledningsevne rapporteres også undertiden med hensyn til den indre permeabilitet, \(k\), med enheder af darcys eller cm2. Det fulde interval af værdier for hydraulisk ledningsevne er 1-10-13 \(\frac{m}{s}\). Eksperimenter som Darcy ‘ s bruges til at måle K i rigtige materialer.

udladningshastigheden \(s\) er en volumenstrøm (\(m^3/S\)), men vi tænker normalt på væskestrøm i form af en hastighed eller hastighed. Udledningsspørgsmålene kan omarrangeres ved at dividere gennem området for at definere Darcy-strømmen

\ \]

eller med hensyn til den indre permeabilitet og trykgradient,

\

hvor \(\ETA\) er væskeviskositeten (se nedenfor for afledning af den anden ligning).

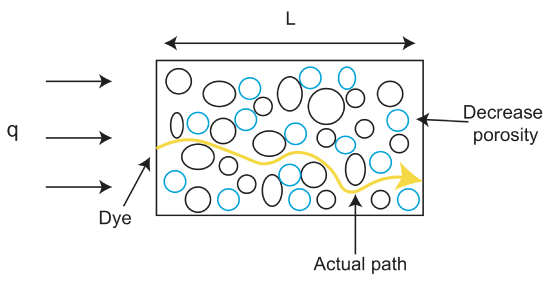
det er vigtigt at bemærke, at Darcy-strømmen ikke svarer til væskehastigheden, selvom den er i hastighedsenheder. Væskehastigheden findes gennem den gennemsnitlige lineære hastighed (\(v_a\)), som er gennemsnittet af hastigheden af alle mulige væskeveje gennem det porøse medium: men at finde denne værdi er uden for denne klasse. I stedet vil vi bemærke, at væskehastigheden er

\

hvor \(\varphi\) er porøsiteten og v er væskehastigheden. Porøsiteten, \(\varphi\) beregnes som forholdet mellem volumen af tomrum og det samlede volumen af et materiale \(\varphi=\frac{V_{void}}{V_{tot}}\) og udtrykkes normalt som en brøkdel mellem 0 og 1 eller som en procent. Bemærk, at hvis \(\varphi\lekv\) 1 så er væskehastigheden større darcy-strømmen.

et andet udtryk, der opstår, når man diskuterer strømning gennem klipper og ukonsoliderede materialer, er permeabilitet. Mens porøsitet er den faktiske brøkdel af porer (hulrum) i klippen, kan disse hulrum have forskellige former og forskellige tilslutningsmuligheder, hvilket påvirker, hvor let en væske kan bevæge sig gennem porerummet. Permeabiliteten er et mål for den lethed, hvormed væsker og gasser kan passere gennem en sten. Jo mere konsolideret materialet er, desto lavere er dets permeabilitet. Således har “løse” materialer som grus høj permeabilitet. Nogle klipper kan også have anisotrop permeabilitet, hvilket betyder, at væsker let kan strømme i en retning, men ikke i en anden. Et eksempel på en sten med anisotrop permeabilitet er en skifer. Væsker kan bevæge sig let inden for et lag af skifer, men kan ikke bevæge sig på tværs af lag.

hydraulisk hoved

Tilbage til Darcy ‘ s eksperimenter, hvad er fysisk proces, der faktisk driver væskestrømmen gennem flume?

udtrykket \(\frac{dh}{dh} \) kaldes det hydrauliske hoved, som er væsketrykket på grund af vægten af en væske i forhold til en eller anden referenceplacering: en trykgradient. Imidlertid har \(\frac{dh}{dh} \) ikke Enheder med et tryk pr. enhedslængde, så hvorfor kaldes det hydraulikhovedet?

lad os overveje, hvad trykket er i flume i Darcy ‘ s eksperimenter. For at udføre eksperimenterne havde Darcy en vandtank i den øverste ende af røgen, der gav et konstant vandniveau øverst på ruden, svarende til rømmens højde, \(h_1\). Tilsvarende var der en tank i bunden med et konstant vandniveau svarende til \(h_2\). Derfor er væsketrykket i hver af tankene på grund af vandets vægt givet af \(P = \rho g h\). Trykgradienten mellem toppen og bunden af plume er derefter

\

eller

\

erstatter Darcy ‘ s Lov,

\& =\frac{K}{\rho g}\frac{dp}{DKs} \end{align}. \ ]

husk ovenfra, at den hydrauliske ledningsevne kan skrives i form af den indre permeabilitet som \(K = k\frac{\gamma}{\eta}\), hvilket svarer til \(k\frac{\rho g}{\ETA} \) eller omarrangering, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Derfor kan vi erstatte med at give to ækvivalente udtryk for Darcy ‘s Lov, med et interms af gradienten i højden,

\

og det andet med hensyn til gradienten i tryk,

\

således \(\frac{dh}{dh}\) kaldes det hydrauliske hoved, fordi den fysiske Oprindelse af udtrykket i Darcy’ s Lov er trykgradienten i væsken, som driver strømmen.

vand, der forlader en akvifer

lad os nu lave et eksempel, der beregner væskehastigheden af vand, der kommer ind i en akvifer. På skitsen under akviferhøjden følger topografien på bakken ved siden af dalen med strømmen. Vand strømmer fra højt tryk (Hovedhøjde) mod dalen og forlader akviferen ved strømmen. Vi kan bruge Darcy ‘ s lov til at estimere hastigheden af vandstrømmen fra akviferen.

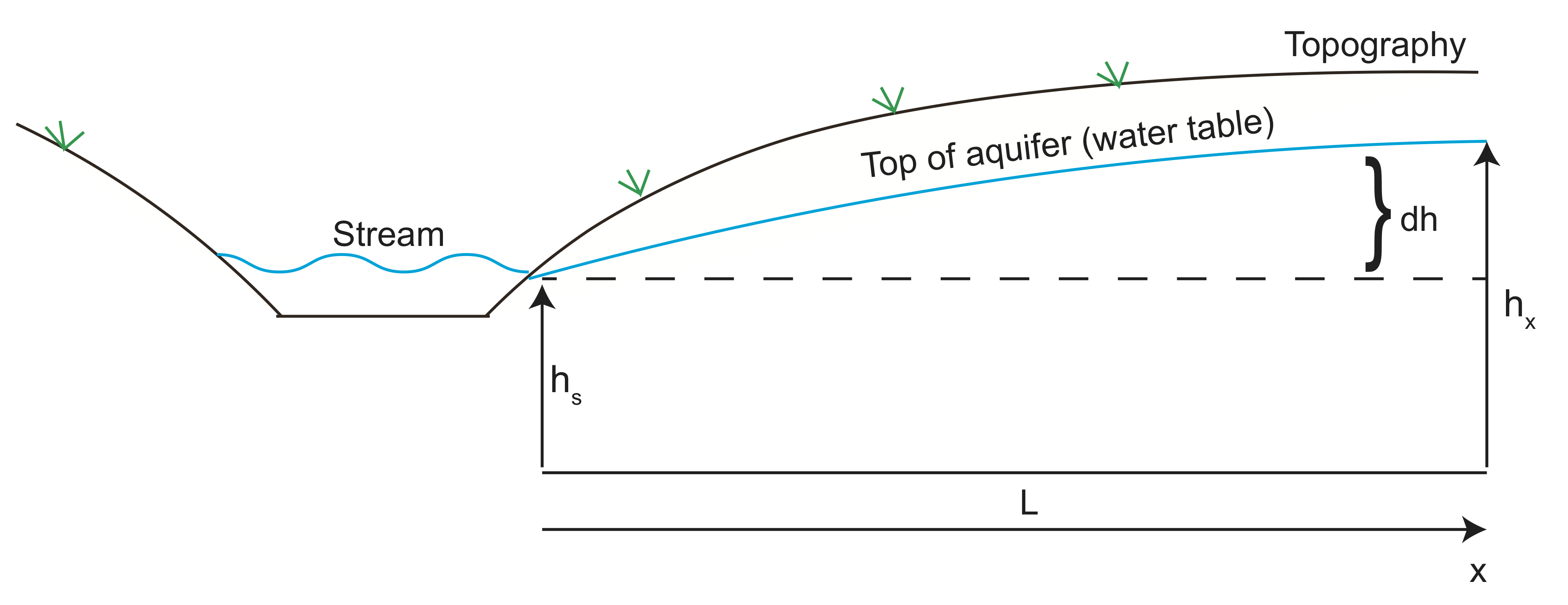
Ved hjælp af geofysisk billeddannelse findes akviferens højde at være 10 m (\(dh\)) over strømhøjden omkring 100 meter (\(L\)) væk. Antag, at den hydrauliske ledningsevne er \ (K=10^{-6}\) m/s, og porøsiteten er \(\varphi=30\)%.

darcy-strømmen er

\

\

Laminar versus Turbulent strøm

en af de implicitte antagelser i Darcy ‘ s lov er, at strømmen er laminar. Laminær strømning er karakteriseret som bestående af tynde lag eller laminer af væske, der alle bevæger sig parallelt med hinanden. I modsætning turbulent strøm er kendetegnet ved hvirvler, hvirvler og hvirvler, hvor tilstødende lag af væske divergerer og tage forskellige veje ned strøm.

en måde, hvorpå vi kan kvantificere, om en væske er laminær eller turbulent, er ved at beregne Reynolds tal for strømmen, defineret som

\

Reynolds tal findes ved at overveje de to udtryk i momentumbalancen for strømmen. Volumenenhed, som driver strømmen, \(\rho u \ frac{du}}\). Volumenenhed, som modstår strømning, \(\eta \ frac{d^2U}{DH^2}\). Disse to udtryk skal balancere, så vi kan sætte dem lige,

\

dernæst omskriver vi udtrykkene på en forenklet måde for kun at fange de relevante dimensioner af variablerne. For at gøre det gennemgår vi det, der kaldes en dimensionel analyse, hvor vi erstatter hver variabel med en referenceværdi, gange en ikke-dimensionel form af variablen.

for eksempel for udtrykket \(h\) omskrives som bare \(L\’\), hvor\ (L\) er referencelængden(væskedybden) og\ (H’\) er den ikke-dimensionelle afstand. Tilsvarende lader vi \(u = u_o u’\). Ved at erstatte disse i ligningen får vi

\

dernæst kombinerer vi de konstante værdier foran

\

Bemærk, at kombinationen af variabler foran er Reynolds tal

\

hvor variablerne er\ (u_o\) strømningshastighed, l væskedybde og de variabler, vi har set tidligere, \(\rho\) væsketæthed og \(\ETA\) væskeviskositet. Ved at gennemgå denne analyse finder vi, at enhver strøm, der er kendetegnet ved balancen mellem disse to udtryk, kan sammenlignes ved blot at kende værdien af Reynolds’ nummer. For eksempel, hvis en strøm har en viskositet, der er 10 gange viskositeten i en anden strøm, vil de to strømme opføre sig det samme, hvis densiteten (eller hastigheden eller længden) også øges med en faktor på 10 for den højere viskositetssag; det vil sige Reynolds-tallet for de to strømme er det samme.

for at have Darcy-strøm skal Reynolds tal være mindre end omkring 1-10 (laminar). For \(Re > 1-10 \) er strømmen ikke strengt laminær, men den er endnu ikke turbulent (ikke-lineær, ikke-laminær). For at have turbulent strøm skal Reynolds tal være større end omkring 2000.

forståelse af, at konstanterne i tælleren og nævneren påvirker strømningens egenskaber på den modsatte måde, hjælper også med at tænke på, hvordan forskellige væsker vil opføre sig under lignende ydre forhold. For eksempel vil en tættere væske, der også har en hurtig hastighed, have en højere Re og udvise turbulent opførsel. I modsætning hertil vil en væske som is, der har en høj viskositet og bevæger sig meget langsomt, have en lav Re og vil sandsynligvis have laminær strømning. Isens høje viskositet virker for at stabilisere strømmen. Som et andet eksempel kan to væsker begge bevæge sig med samme hastighed opføre sig anderledes, hvis de andre værdier i Reynolds tal \(\frac{\rho L}{\mu}\) er forskellige. Derfor afhænger strømningstypen ikke kun af strømningshastigheden, men af kombinationen af variabler i Reynolds nummer.

anvendelse af Darcy ‘s strøm

Darcy’ s lov er den vigtigste ligning, der styrer strømmen i akviferer og brønde. Uden det ville vi ikke være i stand til at bore brønde eller forstå vandbevægelse i akviferer, især i Californiens central valley, hvor begge disse ideer er afgørende for både landbrugsproduktivitet og grundvandssænkning.