Regrese k průměru je běžný statistický jev, který může uvést v omyl nás, když pozorujeme svět. Naučit se rozpoznat, kdy regrese k průměru je ve hře nám může pomoci vyhnout se špatnou interpretací údajů a vidět vzory, které neexistují.

* * *

je důležité minimalizovat případy špatného úsudku a řešit slabá místa v našem uvažování. Učení o regresi k průměru nám může pomoci.

nositel Nobelovy ceny psycholog Daniel Kahneman napsal knihu o předsudky, které cloud naše uvažování a narušují naše vnímání reality. Ukazuje se, že existuje celá řada logických chyb, kterých se dopouštíme, protože naše intuice a mozky se nezabývají jednoduchými statistikami. Jednou z chyb, které zkoumá při rychlém a pomalém myšlení, je neslavná regrese směrem k průměru.

pojem regrese k průměru nejprve vypracoval Sir Francis Galton. Pravidlo platí, že v každé sérii se složitými jevy, které jsou závislé na mnoha proměnných, kde se jedná o náhodu, mají extrémní výsledky tendenci následovat mírnější.

Při Hledání Moudrosti, Peter Bevelin nabízí například John, který byl nespokojený s výkonem nových zaměstnanců, tak je dal do dovedností-posílení program, kde změřil dovedností zaměstnanců:

Jejich skóre jsou nyní vyšší, než byly na první test. Johnův závěr: „program zvyšující dovednosti způsobil zlepšení dovedností.“To nemusí být nutně pravda. Jejich vyšší skóre by mohlo být výsledkem regrese k průměru. Od těchto jedinců byla měřena jako na nízké konec rozsahu dovednosti, které by prokázaly zlepšení, i když nevzali dovedností-posílení programu. A mohlo by existovat mnoho důvodů pro jejich dřívější výkon — stres, únava, nemoc, rozptýlení atd. Jejich skutečná schopnost se možná nezměnila.

náš výkon se vždy pohybuje kolem nějakého průměrného skutečného výkonu. Extrémní výkon má tendenci být příště méně extrémní. Proč? Testovací měření nikdy nemohou být přesná. Všechna měření se skládají z jedné skutečné části a jedné náhodné chybové části. Pokud jsou měření extrémní, pravděpodobně budou částečně způsobena náhodou. Šance pravděpodobně přispěje méně při druhém měření výkonu.

Pokud přejdeme z jednoho způsobu, jak něco dělat, pouze proto, že jsme neúspěšní, je velmi pravděpodobné, že příště uděláme lépe, i když nový způsob, jak něco udělat, je stejný nebo horší.

To je jeden z důvodů, proč je nebezpečné extrapolovat z malé velikosti vzorku, protože data nemusí být reprezentativní pro distribuci. To je také důvod, proč James March tvrdí, že čím déle někdo zůstane ve své práci, “ tím menší je pravděpodobný rozdíl mezi pozorovaným záznamem výkonu a skutečnými schopnostmi.“V krátkodobém horizontu se může stát cokoli, zejména v jakémkoli úsilí, které zahrnuje kombinaci dovedností a štěstí. (Poměr dovednosti ke štěstí také ovlivňuje regresi k průměru.)

Regrese k průměru

účinky regrese k průměru může být často pozorovány ve sportu, kde efekt způsobuje spoustu neopodstatněných spekulací.

V Myšlení Rychlé a Pomalé Kahneman připomíná sledování pánské lyžařské skok, disciplína, kde konečné skóre je kombinací dvou samostatných skoků. Kahneman si byl vědom regrese k průměru a byl překvapen, když slyšel předpovědi komentátora o druhém skoku. Píše:

Norsku měl skvělý první skok; on bude nervózní, v naději, že chránit jeho vedení a bude pravděpodobně dělat horší“ nebo „Švédsko měl špatný první skok a teď už ví, že nemá co ztratit a bude uvolněný, která by měla pomoci ho udělat lepší.

Kahneman poukazuje na to, že komentátor si všiml, regrese k průměru a přijít s příběhem, pro který neexistuje žádná příčinná důkazy (viz narativní klam). Tím nechci říci, že jeho příběh nemohl být pravdivý. Možná, kdybychom měřili srdeční frekvence před každým skokem, viděli bychom, že jsou uvolněnější, pokud by první skok byl špatný. O to však nejde. Jde o to, regrese k průměru se stane, když štěstí hraje roli, jako tomu bylo ve výsledku prvního skoku.

lekce ze sportu se vztahuje na jakoukoli činnost, kde hraje roli náhoda. Často připojujeme vysvětlení našeho vlivu na konkrétní proces k pokroku nebo jeho nedostatku.

ve skutečnosti je věda o výkonu složitá, závislá na situaci a často je většina toho, co si myslíme, že je pod naší kontrolou, skutečně náhodná.

v případě skoků na lyžích silný vítr proti skokanům povede k tomu, že i ten nejlepší sportovec vykazuje průměrné výsledky. Podobně silný vítr a lyžařské podmínky ve prospěch průměrného skokana mohou vést ke značnému, ale dočasnému nárazu do jeho výsledků. Tyto účinky však zmizí, jakmile se podmínky změní a výsledky se vrátí zpět do normálu.

to může mít vážné důsledky pro koučování a sledování výkonu. Pravidla regrese naznačují, že při hodnocení výkonu nebo náboru, musíme se spoléhat na záznamy více než na výsledky konkrétních situací. Jinak jsme náchylní být zklamáni.

Když Kahneman přednášel izraelskému letectvu o psychologii efektivního výcviku, jeden z důstojníků se podělil o své zkušenosti, že rozšíření chvály na jeho podřízené vedlo k horšímu výkonu, zatímco nadávání vedlo ke zlepšení následného úsilí. V důsledku toho začal být velkorysý s negativní zpětnou vazbou a stal se spíše opatrný, aby příliš chválil.

Kahneman si okamžitě všiml, že jde o regresi k průměru v práci. Mylnou představu ilustroval jednoduchým cvičením, které si možná budete chtít vyzkoušet. Nakreslil kruh na tabuli a poté požádal důstojníky jeden po druhém, aby hodili kousek křídy do středu kruhu zády k tabuli. Poté experiment zopakoval a zaznamenal výkon každého důstojníka v prvním a druhém pokusu.

přirozeně, ti, kteří si vedli neuvěřitelně dobře na první pokus, měli tendenci dělat horší na druhý pokus a naopak. Klam se okamžitě stal jasným: změna výkonu nastává přirozeně. To je nechci říci, že zpětná vazba nezáleží vůbec – možná to dělá, ale důstojník neměl žádné důkazy k závěru, že ano.

Nedokonalé Korelace a Šance

V tomto bodě, můžete se zeptat, proč regrese k průměru se stane, a jak se můžeme ujistit, že jsme si vědomi, když to nastane.

abychom pochopili regresi k průměru, musíme nejprve pochopit korelaci.

korelační koeficient mezi dvěma opatřeními, která se pohybuje mezi -1 a 1, je mírou relativní váhu faktorů, které sdílejí. Například, dva jevy s několika sdílenými faktory, jako je spotřeba balené vody versus míra sebevražd, by měl mít korelační koeficient blízký 0. To znamená, že pokud jsme se podívali na všechny země světa a vynese sebevražd konkrétní rok proti na jednoho obyvatele spotřeba balené vody, děj by se ukázat, ne vzor.

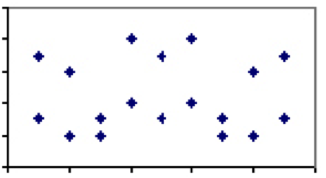
naopak, tam jsou opatření, která jsou výhradně závislé na stejný faktor. Dobrým příkladem je teplota. Jediný faktor určující teplotu-rychlost molekul-sdílí všechny stupnice, proto každý stupeň Celsia bude mít přesně jednu odpovídající hodnotu ve Fahrenheita. Proto teplota ve stupních Celsia a Fahrenheita bude mít korelační koeficient 1 a děj bude přímka.

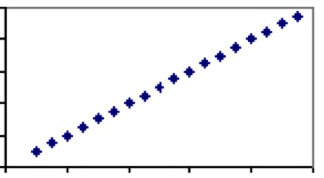
Existuje jen málo, pokud nějaké jevů ve společenských vědách, které mají korelační koeficient 1. Existují, nicméně, spousta případů, kdy je asociace slabá až střední a mezi těmito dvěma jevy existuje určitá vysvětlující síla. Zvažte korelaci mezi výškou a hmotností, která by přistála někde mezi 0 a 1. Zatímco prakticky každý tříletý bude lehčí a kratší než každý dospělý muž, ne všichni dospělí muži nebo tříleté děti stejné výšky budou vážit stejně.

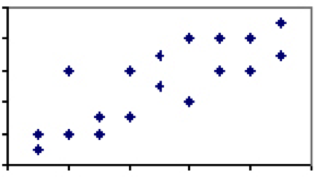
Tento variace a odpovídající nižší stupeň korelace znamená, že zatímco výška je obecně dobrým ukazatelem, tam jasně jsou i jiné faktory, než je výška ve hře. Když je korelace dvou opatření méně než dokonalá, musíme dávat pozor na účinky regrese na průměr.

Kahneman dodržel obecné pravidlo: kdykoli je korelace mezi dvěma skóre nedokonalá, dojde k regresi k průměru.

To se zpočátku může zdát matoucí a ne příliš intuitivní, ale stupeň regrese k průměru přímo souvisí se stupněm korelace proměnných. Tento efekt lze ilustrovat jednoduchým příkladem.

Předpokládejme, že jste na večírku a zeptejte se, proč je to tak, že vysoce inteligentní ženy mají tendenci si vzít muže, kteří jsou méně inteligentní než oni. Většina lidí, dokonce i ti, s některými školení v oblasti statistiky, se rychle skočit s různými kauzální vysvětlení od vyhýbání se konkurenci na obavy z osamělosti, že tyto ženy čelit. Téma takové diskuse pravděpodobně vyvolá velkou debatu.

Co kdybychom se zeptali, proč je korelace mezi inteligenčními skóre manželů méně než dokonalá? Tato otázka je sotva tak zajímavá a není co hádat-všichni víme, že je to pravda. Paradox spočívá v tom, že obě otázky jsou algebraicky ekvivalentní. Kahneman vysvětluje:

Pokud je korelace mezi inteligencí manželů je méně než dokonalé (a pokud se muži a ženy v průměru neliší v inteligenci), pak se jedná o matematické nevyhnutelnosti, že vysoce inteligentní ženy budou manželé manželé, kteří jsou v průměru méně inteligentní než oni (a naopak, samozřejmě). Pozorovaná regrese k průměru nemůže být zajímavější nebo vysvětlitelnější než nedokonalá korelace.

za Předpokladu, že korelace je nedokonalé, šance, že dva partneři zastupující top 1%, pokud jde o nějaké charakteristické je daleko menší než jeden partner, zastupující top 1% a druhý – na dno 99%.

příčina, účinek a léčba

při pokusu o stanovení kauzality mezi dvěma faktory bychom měli být obzvláště opatrní při regresi k průměrnému jevu. Kdykoli je korelace nedokonalá, zdá se, že nejlepší se vždy zhorší a nejhorší se časem zlepší, bez ohledu na jakékoli další ošetření. To je něco, co obecná média a někdy dokonce vyškolení vědci nedokážou rozpoznat.

zvažte příklad, který Kahneman dává:

Depresivní děti léčené energetickým nápojem se během tříměsíčního období výrazně zlepšily. Vymyslel jsem si tento novinový titulek, ale skutečnost, že hlásí, je pravda: pokud jste nějakou dobu léčili skupinu depresivních dětí energetickým nápojem, vykazovali by klinicky významné zlepšení. To je také případ, že Depresivní děti, které tráví nějaký čas stojící na hlavě nebo obejmout kočku po dobu dvaceti minut denně, také projeví zlepšení.

vždy, když přijde po takové titulky je velmi lákavé skočit k závěru, že energetické nápoje, stojící na hlavě nebo objímání kočky jsou naprosto životaschopné léky na deprese. Tyto případy však opět ztělesňují regresi k průměru:

Depresivní děti jsou extrémní skupinou, jsou více depresivní než většina ostatních dětí—a extrémní skupiny v průběhu času ustupují k průměru. Korelace mezi skóre deprese na po sobě jdoucích příležitostech testování je méně než dokonalé, takže tam bude regrese k průměru: depresivní děti budou mít poněkud lepší v průběhu času, i když se obejmout žádné kočky a pít Red Bull.

často mylně připisujeme konkrétní politiku nebo léčbu jako příčinu efektu, kdy by ke změně v extrémních skupinách došlo stejně. To představuje zásadní problém: jak můžeme vědět, zda jsou účinky skutečné nebo jednoduše kvůli variabilitě?

Naštěstí Existuje způsob, jak rozeznat mezi skutečným zlepšením a regresí k průměru. To je zavedení takzvané kontrolní skupiny, která se má zlepšit pouze regresí. Cílem výzkumu je zjistit, zda se léčená skupina zlepšuje více, než může vysvětlit regrese.

V reálných životních situacích s výkonem konkrétních jednotlivců nebo týmů, kde jediným skutečným měřítkem je výkonnost v minulosti a žádné kontrolní skupiny mohou být zavedeny, účinky regrese může být obtížné, ne-li nemožné, odlišit. Můžeme porovnat s průměrem, vrstevníky v kohortě skupiny nebo historické sazby zlepšení, ale žádný z těchto jsou ideální opatření.

***

Naštěstí, povědomí o regresi k průměru jev sám o sobě je již první velký krok směrem k více opatrný přístup k pochopení, štěstí a výkonnost.

Pokud existuje něco, co se dá naučit z regrese k průměru, je to důležitost záznamů, spíše než spoléhat se na jednorázové příběhy o úspěchu. Doufám, že až příště narazíte na extrémní kvalitu částečně řízenou náhodou, uvědomíte si, že účinky se pravděpodobně časem ustupují a podle toho upraví vaše očekávání.

co číst dál

• upgradujte své myšlení pomocí 113 mentálních modelů.
• Přečtěte si o myšlení druhé úrovně, abyste se vyhnuli negativním důsledkům.