Poznámka

následující student výzkumná zpráva byla připravena pro Profesora Judit Kardos‘ Matematika 255 třídy, která se konala na College of New Jersey. Jednalo se o 3-kreditní úvodní kurz v historii matematiky. Tato zpráva byla započítána do 30% konečné známky. Je to příklad toho, jaký druh historického výzkumu mohou studenti dělat pomocí sekundárních zdrojů.

Leonard Euler je Řešení Königsberg Mostu Problém

Königsberg

Náš příběh začíná v 18. století, v malebné město Königsberg, Prusko na břehu Řeky Pregel. V 1254, rytířů založil město Königsberg pod vedením Českého Krále Ottoker II po jejich druhé křížové výpravy proti Prusům. Ve středověku se Königsberg stal velmi důležitým městem a obchodním centrem se svou polohou strategicky umístěnou na řece. Umělecká díla z osmnáctého století ukazují Königsberg jako prosperující město, kde flotily lodí vyplňují Pregel, a jejich obchod nabízí pohodlný životní styl místním obchodníkům i jejich rodinám. Zdravé ekonomice dovoleno lidé z města vybudovat sedm mostů přes řeku, z nichž většina připojen na ostrově Kneiphof, jejich umístění může být vidět v doprovodném obrázku .

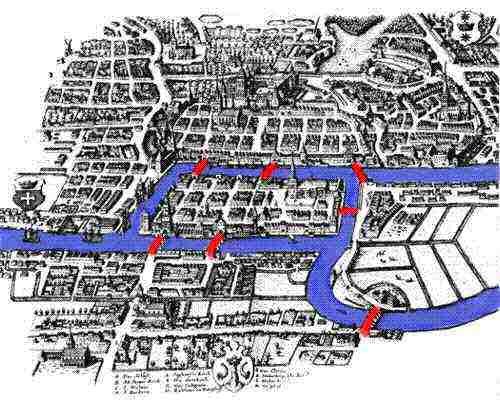
Jako řeka tekla kolem Kneiphof, což doslova znamená hospodě, na dvoře, a další ostrov, je rozděleno město do čtyř různých oblastí. Sedm mostů se nazývalo Kovářův most, spojovací most, zelený most, kupecký Most, dřevěný most, vysoký most a medový most. Podle tradice trávili občané Königsbergu nedělní odpoledne procházkami po svém krásném městě. Při chůzi, lidé z města se rozhodl vytvořit hru pro sebe, jejich cílem je vymyslet způsob, ve kterém by mohli chodit po městě, přes každý ze sedmi mosty pouze jednou. I když žádný z občanů Königsbergu nemohl vymyslet trasu, která by jim umožnila překročit každý z mostů pouze jednou, stále nemohli dokázat, že to není možné. Naštěstí pro ně nebyl Königsberg příliš daleko od Petrohradu, domova slavného matematika Leonarda Eulera.

Euler a můstkový problém

proč by se Euler zabýval problémem tak nesouvisejícím s matematikou? Proč by takový skvělý matematik trávil hodně času s triviálním problémem, jako je problém mostu Königsberg? Euler byl zjevně zaneprázdněný muž, během svého života vydal více než 500 knih a dokumentů. V roce 1775 sám, napsal v průměru jeden matematický papír týdně, a během svého života psal o různých tématech kromě matematiky, včetně mechaniky, optiky, astronomie, navigace a hydrodynamiky. Není divu, že Euler se cítil tento problém byl triviální, uvádí v roce 1736 dopis Carl Leonhard Gottlieb Ehler, starosta města Danzig, který se ho zeptal na řešení problému :

. . . Tak vidíte, nejvznešenější Pane, jak si tento typ řešení nese malý vztah k matematice, a já nechápu, proč čekáš, že matematik vyrábět to, spíše než kdokoli jiný, pro řešení je založeno na důvodu, a jeho objev není závislá na žádné matematické zásady. Z tohoto důvodu nevím, proč i otázky, které mají tak malý vztah k matematice, řeší matematici rychleji než ostatní.

přestože Euler považoval problém za triviální, stále ho to zaujalo. V dopise téhož roku Giovanni Marinoni, italský matematik a inženýr, Euler řekl ,

Tato otázka je tak banální, ale zdálo se mi, hodné pozornosti, že v geometrii, ani algebru ani umění počítání byla dostatečná, aby to vyřešit.

Euler věřil, že toto byl problém týkající se tématu, které Gottfried Wilhelm Leibniz kdysi diskutovali a toužil pracovat, něco Leibniz označuje jako geometria situs, nebo geometrie polohy. Tato takzvaná geometrie polohy je to, co se nyní nazývá teorie grafů, kterou Euler zavádí a využívá při řešení tohoto slavného problému.

Eulerův důkaz

26. srpna 1735 představuje Euler dokument obsahující řešení problému Konigsbergova mostu. Zabývá se jak tímto konkrétním problémem, tak obecným řešením s libovolným počtem pevností a libovolným počtem mostů. Tento dokument nazvaný „Solutio problematis ad geometriam situs pertinentis“ byl později publikován v roce 1741 . Eulerova práce je rozdělena do jednadvaceti číslovaných odstavců a v následujícím textu bude představena zjednodušená verze eulerových odstavců.

v prvních dvou odstavcích Eulerova důkazu představuje problém mostu Konigsberg. V Odstavci 1, Euler uvádí, že je přesvědčen, že tento problém se týká geometrie, ale ne geometrie dobře známý tím, že jeho současníci, který zahrnuje měření a výpočty, ale místo toho nový druh Geometrie, které Leibniz označuje jako Geometrie Polohy. V odstavci 2 pak Euler vysvětluje svému publiku, jak problém Konigsberg funguje. Euler za předpokladu, náčrt problému (viz Eulerovo Číslo 1), a nazývá sedmi různých mostů: a, b, c, d, e, f, a, g. V tomto odstavci se uvádí obecnou otázku, problém, „Může jeden zjistit, zda je či není možné, aby přes každý most právě jednou?“

Eulerovo Číslo 1 z ‚Solutio problematis ad geometriam situs pertinentis,‘ Eneström 53

Poté, uvádějící obecnou otázku se snaží vyřešit, Euler začne zkoumat různé metody hledání řešení. V Odstavci 3, Euler říká čtenáři, že, jak vyřešit tento konkrétní problém, mohl by napsat všechny možné cesty, ale tato technika bude trvat hodně času, a nebude pracovat pro větší konfigurace s více mosty a pevnin. Kvůli těmto problémům se Euler rozhodl zvolit jinou metodu řešení tohoto problému.

V Odstavci 4, začne zjednodušení problému tím, že vymýšlejí vhodný systém představují přechod mostu. Euler se rozhodne, že místo toho, aby použil malá písmena k reprezentaci přechodu mostu, napsal velká písmena představující pevninu. Například, odkazující na jeho Obrázek 1, AB by znamenalo, že cesta, která začala v pevnině, a skončil v B. Navíc, když po cestě z pevniny A do bodu B, někdo rozhodne přestěhovat na pevninu D, to by prostě být označeny, ABD. V odstavci 5 Euler pokračuje ve své diskusi o tomto procesu a vysvětluje, že v ABDC, i když existují čtyři velká písmena, byly překročeny pouze tři mosty. Euler vysvětluje, že bez ohledu na to, kolik mostů je, bude ještě jeden dopis, který bude představovat nezbytný přechod. Kvůli tomu celý problém s mostem Königsberg vyžadoval, aby bylo překročeno sedm mostů, a tedy osm velkých písmen.

v odstavci 6 Euler pokračuje ve vysvětlování podrobností své metody. Říká čtenáři, že pokud existuje více než jeden most, který lze překročit při přechodu z jedné pevniny na druhou, nezáleží na tom, který most se používá. Například, i když existují dva mosty, a A b, které mohou vzít cestovatele z A do B, nezáleží na Eulerově notaci, který Most je pořízen. V tomto odstavci Euler také pojednává o konkrétním problému, se kterým se zabývá. Vysvětluje, pomocí jeho původní postava, že Königsberg problém je přesně osm dopisů, kde dvojice (A,B) a (A,C) se musí objevit vedle sebe, přesně dvakrát, bez ohledu na to, které písmeno se objeví jako první. Kromě toho se páry (a, D), (B, D) A (C,D) musí vyskytovat společně přesně jednou, aby existovala cesta, která překračuje každý most jednou a pouze jednou.

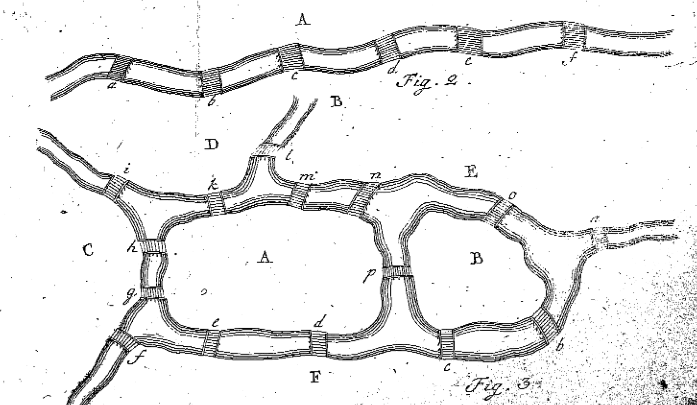
Eulerova Čísla 2 a 3 z ‚Solutio problematis ad geometriam situs pertinentis,‘ Eneström 53

V Odstavci 7, Euler informuje čtenáře, že buď on potřebuje najít osm-dopis sekvence, která splňuje problém, nebo potřebuje dokázat, že žádná taková posloupnost existuje. Než to udělá pro problém s mostem Königsberg, rozhodne se najít pravidlo, aby zjistil, zda existuje cesta pro obecnější problém. Dělá to v odstavci 8 tím, že se podívá na mnohem jednodušší příklad pevniny a mostů. Euler nakreslí obrázek 2 a začne hodnotit situace, kdy prochází region A. Euler uvádí, že pokud most je jednou cestoval, byl buď tam, kde cesta začala nebo skončila, a proto byl použit pouze jednou. Pokud jsou mosty a, b A c cestovány jednou, použije se a přesně dvakrát, bez ohledu na to, zda se jedná o počáteční nebo koncové místo. Podobně, pokud by pět mostů vedlo k A, pevnina A by se během cesty vyskytla přesně třikrát. Euler uvádí, že “ obecně platí, že pokud je počet mostů libovolný lichý počet a pokud se zvýší o jeden, pak je počet výskytů A polovina výsledku.“Jinými slovy, pokud existuje lichý počet mostů připojení k jiné části pevniny, přidat jeden do počtu mostů, a to vydělit dvěma, aby se zjistit, kolik celkové časy musí být použity v cestě, kde každý most je použit pouze jednou a pouze jednou (tj. Celkový výskyt A, kde A má lichý # mostů = (#mostů – 1) / 2).

pomocí této skutečnosti Euler řeší problém königsbergova mostu v odstavci 9. V takovém případě, protože existuje pět mostů, které vedou k A, musí se vyskytnout třikrát (viz jeho Obrázek 1 výše). Podobně se B, C A D musí objevit dvakrát, protože všechny mají tři mosty, které k nim vedou. Proto 3 (Pro A) + 2 (Pro B) + 2 (pro C) + 2 (pro D) = 9, ale Euler již uvedl, že pro sedm mostů musí být pouze osm výskytů. To je rozpor! Proto není možné cestovat po mostech ve městě Königsberg jednou a jen jednou. Konec, nebo je? Zatímco lidé z Königsbergu mohou být s tímto řešením spokojeni, velký matematik Leonhard Euler nebyl spokojen. Euler dále pokračuje ve svém důkazu, aby se zabýval obecnějšími situacemi.

Eulerovo Zobecnění

V Odstavci 10, Euler pokračuje ve své diskusi tím, že pokud se situace týká všech zemských s lichým počtem mostů, je možné říci, zda cesta může být provedeno pomocí každý most pouze jednou. Euler uvádí, že pokud je součet počtu, kolikrát se musí každé písmeno objevit, ještě jeden, pak celkový počet mostů, může být provedena cesta. Pokud je však počet výskytů větší než jeden více než počet mostů, nelze provést cestu, jako je problém s mostem Königsberg. Je to proto, že pravidlo, které Euler dává pro lichý počet mostů, pomocí jeho Obrázek 2, platí pro obecné situace, zda existuje pouze jedna pevnina nebo více než jeden.

v odstavcích 11 a 12 se Euler zabývá situací, kdy má Region k němu připojen sudý počet mostů. Tato situace se neobjevuje v problému Königsbergu, a proto byla dosud ignorována. V situaci s pevninou X se sudým počtem mostů mohou nastat dva případy. První případ je, když X je výchozím bodem pro cestu. V tomto případě se X objeví dvakrát, jednou jako výchozí bod a znovu jako koncový bod. V druhém případě X není výchozím bodem. Pokud by k tomu došlo, X by se objevil pouze jednou, protože cesta by musela vstoupit přes jeden most a okamžitě opustit jediný dostupný. Podobně, pokud jsou k X připojeny čtyři mosty, počet výskytů X závisí na tom, zda se jedná o výchozí bod. Pokud cesta začíná v X, musí se objevit třikrát, ale pokud nezačne v X, objeví se pouze dvakrát. Takže obecně, pokud X má sudý počet připojených mostů, pak pokud cesta nezačne v X, X se objeví poloviční počet mostů (tj. Výskyty X, kde X je sudý a ne výchozí bod = (#mostů) / 2). Pokud cesta začíná v X, pak X se objeví polovina počtu mostů plus jedna (tj. výskyty X, kde X je sudý a počáteční bod = ((#mostů) / 2) + 1).

v odstavcích 13 až 15 Euler vysvětluje, jak zjistit, zda existuje cesta používající každý most jednou a pouze jednou, a představuje svůj vlastní příklad, aby ukázal, jak to funguje. Euler první vysvětluje jeho jednoduchý šest-krok způsob, jak vyřešit nějaké obecné situaci se pevnina rozdělena podle řeky a spojeny mosty. První Euler označuje každou pevninu velkým písmenem. Za druhé vezme celkový počet mostů, přidá jeden a zapíše to nad graf, který se chystá udělat. Dále vezme velká písmena, vloží je do sloupce a vedle nich zapíše počet mostů. Začtvrté označuje hvězdičkami pozemní hmoty, které mají sudý počet mostů. Pak vedle každého sudého čísla zapíše ½ čísla a vedle každého lichého čísla umístí ½ čísla plus jedno. Nakonec Euler přidá čísla zapsaná v pravém sloupci a pokud je součet o jeden menší než nebo roven počtu mostů plus jeden, pak je možná požadovaná cesta. Je však důležité si uvědomit, že pokud je součet o jeden menší než počet mostů plus jeden, musí cesta začít od jedné z pevnin označených hvězdičkou. Pokud se součet rovná počtu mostů plus jeden, musí cesta začít v oblasti, která není označena hvězdičkou.

příklady

použití problému Konigsberg jako jeho první příklad Euler ukazuje následující:

Počet mostů = 7, Počet mostů plus jedna = 8

Oblast Mosty Krát Regionu se Musí Objevit

5-3

B 3 2

C 3 2

D 3 2

Nicméně, 3 + 2 + 2 + 2 = 9, což je více než 8, takže cesta je nemožné.

vzhledem k tomu, že tento příklad je spíše základní, Euler se rozhodne navrhnout svou vlastní situaci se dvěma ostrovy, čtyřmi řekami a patnácti mosty. Situaci, kterou Euler vytvořil, lze vidět na jeho obrázku 3 výše. Euler se nyní pokouší zjistit, zda existuje cesta, která umožňuje někomu projít každý most jednou a jen jednou. Euler následuje stejné kroky jako výše, pojmenování pěti různých regionech s velkými písmeny, a vytvoří tabulku podívat se na to, pokud je to možné, jako je následující:

Počet mostů = 15, Počet mostů plus jedna = 16

Oblast Mosty Krát Regionu se Musí Objevit

* 8 4.

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3.

kromě, 4 + 2 + 2 + 2 + 3 + 3 = 16, což se rovná počtu mostů, plus jedna, což znamená, že cesta je, ve skutečnosti, je to možné. Protože součet se rovná počtu mostů plus jeden, cesta musí začít buď v D nebo e. Nyní, když Euler ví, že je možné podniknout cestu, vše, co musí udělat, je uvést, jaká bude cesta. Euler si vybere cestu EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, kde zahrnuje mosty, které se kříží mezi písmeny představujícími pevninu. I když jsou tyto informace cizí, protože přesný most nezáleží na tom, že je cesta možná, je to užitečné při výběru cesty. Toto je dobrý příklad, který ukazuje metodu, kterou by Euler použil při řešení jakéhokoli problému této povahy.

Eulerovo Závěry

V následujících několika odstavcích, Euler představuje další způsob, jak zjistit, jestli cesta může být dán jakýkoliv soubor zemských, mosty a řeky. V odstavci 16 Euler poukazuje na to, že celkový počet čísel uvedených přímo napravo od pevniny činí až dvojnásobek celkového počtu mostů. Tato skutečnost se později stává známou jako lemma handshaking. V podstatě, lemma handshaking uvádí, že každý most se počítá dvakrát, jednou za každou pevninu, ke které je připojen. V odstavci 17 Euler dále uvádí, že součet všech mostů vedoucích do každé oblasti je sudý, protože polovina tohoto počtu se rovná celkovému počtu mostů. To však není možné, pokud existuje lichý počet pevnin s lichým počtem mostů. Proto Euler dokazuje, že pokud jsou k pozemským masám připojena nějaká lichá čísla, musí existovat sudý počet těchto pevnin.

Nicméně, toto není dost, aby prokázal, když tam je cesta, kde každý most je použit pouze jednou a pouze jednou, jako Königsberg Mostu problém má sudý počet zemských s lichým počtem mostů jít k nim. Z tohoto důvodu Euler přidává další omezení v odstavcích 18 a 19. Euler vysvětluje, že od celkového počtu mostů připojeny k sobě pevniny je rovna dvojnásobku počtu mostů (jak je vidět v handshaking lemma), takže proto pokud přidáte dva, aby tento součet pak vydělíme dvěma, dostanete celkový počet mostů plus jedna. Toto číslo je stejné jako číslo použité dříve, které se používá k určení, zda je cesta možná. Pokud jsou všechna čísla sudá, bude třetí sloupec v tabulce součet o jeden menší než celkový počet mostů plus jeden.

Euler pak vysvětluje, že je zřejmé, že pokud existují dvě části pevniny s lichým počtem mostů pak cesta bude vždy možné, pokud cesta začíná v jednom z regionů s lichým počtem mostů. Je to proto, že pokud se sudá čísla sníží na polovinu a každá z lichých se zvýší o jednu a polovinu, součet těchto polovin se rovná ještě jedné než celkovému počtu mostů. Pokud však existují čtyři nebo více pevnin s lichým počtem mostů, pak není možné, aby tam byla cesta. Je to proto, že součet poloviny lichá čísla plus jedna spolu s součet všech poloviny i čísla tak, aby součet třetího sloupce větší než celkový počet mostů plus jedna. Proto Euler právě dokázal, že mohou existovat nanejvýš dvě pevniny s lichým počtem mostů.

s tímto konstatováním může Euler nyní učinit své závěry týkající se obecnějších forem problému mostu Königsberg. V odstavci 20, Euler uvádí tři pokyny, které může někdo použít k určení, zda existuje cesta pomocí každého mostu jednou a pouze jednou. První, tvrdil, že pokud existuje více než dva pevninu s lichým počtem mostů, pak žádná taková cesta je možná. Druhý, pokud je počet mostů lichý pro přesně dvě pozemní masy, pak je cesta možná, pokud začíná v jedné ze dvou lichých očíslovaných pevnin. Konečně, Euler uvádí, že pokud neexistují žádné regiony s lichým počtem pevnin, může být cesta provedena v jakémkoli regionu. Po uvedení těchto tří skutečností, Euler závěru jeho důkaz s Odstavcem 21, který pouze uvádí, že po jednom zjistí, že cesta existuje, ale ještě musí projít úsilí, aby napsat cestu, která funguje. Euler věřil, že způsob, jak toho dosáhnout, je triviální, a nechtěl na tom trávit hodně času. Euler však navrhl soustředit se na to, jak se dostat z jedné pevniny na druhou, místo aby se nejprve soustředil na konkrétní mosty.

Eulerovo Důkaz a Teorie Grafů

Při čtení Euler je původní doklad, objeví poměrně jednoduché a snadno pochopitelné práce z matematiky; nicméně, to není důkaz, ale mezistupně, že se tento problém známý. Euler je velkou inovací bylo v prohlížení Königsberg mostu problém abstraktně, pomocí linek a písmena představují větší situace zemských a mosty. Používal velká písmena k reprezentaci pevniny, a malá písmena k reprezentaci mostů. To byl zcela nový typ myšlení za čas, a v jeho papíru, Euler omylem vyvolala nové odvětví matematiky zvané teorie grafů, kde graf je prostě sbírka vrcholů a hran. Dnes se cesta v grafu, která obsahuje každý okraj grafu jednou a pouze jednou, nazývá Eulerovská cesta, kvůli tomuto problému. Od doby, Euler vyřešil tento problém dnes, teorie grafů, teorie se stala důležitým odvětvím matematiky, která vede základ našeho myšlení o sítích.

Königsberg Most problému je důvod, proč Biggs státy ,

počátky teorie grafů jsou skromné, dokonce frivolní … problémy, které vedly k rozvoji teorie grafů byla často trochu více než hádanky, navržen tak, aby otestovat vynalézavosti, spíše než stimulovat představivost. Ale i přes zdánlivou banalitu, jako puzzle, které zachytil zájem matematiků, s tím výsledkem, že teorie grafů stala předmětem bohaté na teoretické výsledky překvapující rozmanitost a hloubku.

Jako Biggs prohlášení by znamenalo, že tento problém je tak důležité, že to je zmíněno v první kapitole každé Teorie Grafů knihu, která byla prostudoval v knihovně.

Po Euler ‚ s discovery (nebo vynález, v závislosti na tom, jak čtečka vypadá na to), teorie grafů, teorie rozvíjel s hlavními příspěvky velcí matematici jako Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff, a George Polya. Tito muži vše přispělo k odhalení „jen o vše, co je známo o velké, ale nařídil, grafy, jako je mříž tvořená atomy v krystalu nebo hexagonální mřížky vyrobený včelami v úlu .“Další slavné teorie grafů problémy patří najít způsob, jak uniknout z bludiště nebo labyrint, nebo najít pořadí tahů s rytíř na šachovnici tak, že každý čtverec je přistála na pouze jednou a rytíř se vrací do prostoru, na který on začal . Některé další problémy teorie grafů se po staletí nevyřešily .

osud Königsbergu

zatímco teorie grafů vzkvétala poté, co Euler vyřešil problém s mostem Königsbergu, město Königsberg mělo mnohem jiný osud. V roce 1875, lidé z Königsberg se rozhodl postavit nový most, mezi uzly B a C, zvýšení počtu odkazů z těchto dvou zemských na čtyři. To znamenalo, že pouze dvě pozemní masy měly lichý počet odkazů, což dalo poměrně jednoduché řešení problému. Vznik mostu navíc může, ale nemusí být podvědomě způsoben touhou po cestě k vyřešení slavného problému města.

Nicméně, nový most nevyřeší všechny Königsberg budoucí problémy, jako město nečekal, že zpět do devatenáctého století, „smutný a válce-roztrhané osudu, který čekal jako hostitel pro jeden z nejkrutějších bitev druhé světové VÁLKY.“Během čtyř dnů v srpnu 1944 Britské bombardéry zničily staré město i severní část Königsbergu. V lednu a únoru 1945 je oblast kolem Königsbergu obklíčena ruskými silami. Němečtí civilisté se začínají evakuovat z města, ale pohybují se příliš pozdě. Tisíce lidí jsou zabity při pokusu o útěk lodí a pěšky přes ledové vody Curonian Lagoon. V dubnu 1945 dobyla Rudá armáda Königsberg s asi devadesáti procenty starého města ležícího v troskách.

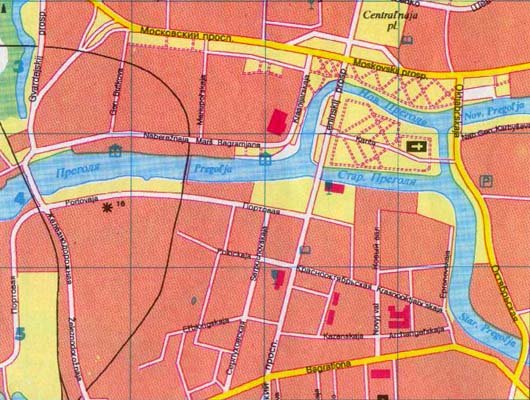
aktuální mapa ulic města Königsberg je uvedena níže . Tato mapa ukazuje, jak moc se město změnilo. Mnoho mostů bylo zničeno během bombardování, a město již nemůže klást stejnou zajímavou otázku, jakou dokázali v osmnáctém století. Spolu s velmi odlišným uspořádáním má město Königsberg nové jméno, Kaliningrad, s řekou Pregel přejmenovanou na Pregolya . Zatímco osud Königsbergu je hrozné, občanů staré kavárně problém křížení každý z jejich staré sedm mostů právě jednou vedl ke vzniku zcela nového odvětví matematiky, teorie grafů.

Biggs, Norman L., E. K. Lloyd, a Robin J. Wilson. Teorie Grafů: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Euler: Pán nás všech. Washington: Matematická asociace Ameriky, 1999.

Euler, Leonhard, ‚Solutio problematis ad geometriam situs pertinentis‘ (1741), Eneström 53, archiv MAA Euler.

“ Dějiny matematiky: on Leonhard Euler (1707-1783).“ScienceWeek (2003). 6.Listopadu. 2005.

Hopkins, Brian a Robin Wilson. „Pravda o Königsbergu.“College Mathematics Journal (2004), 35, 198-207.

“ mosty Konigsberg.“The MacTutor History of Mathematics Archive:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

poznámka Editora: Tento článek byl původně publikován v konvergence, Svazek 3 (2006).