2.5: Darcyho Zákon – Proudění v Porézním prostředí
Darcyho zákon je klíčový k pochopení mnoha oborů geologie, zejména hydrogeologie. Než se podíváme na zákon a na to, co nám může říci, podívejme se na to, jak byl vyvinut. Darcyho zákon je pojmenován po Henry Darcy, 19. století francouzský inženýr, který vyvinul podzemní tlakové potrubí systému dodávat vodu v okolí města Dijon. Systém, který také dodával vodu slavným dijonským fontánám, způsobil revoluci v městských vodovodních a kanalizačních systémech. Systém nevyžadoval žádná čerpadla a byl poháněn čistě gravitací. Během procesu vývoje nového systému provedl Darcy řadu experimentů, kde se pokusil pohybovat vodou pouze pomocí gravitace.
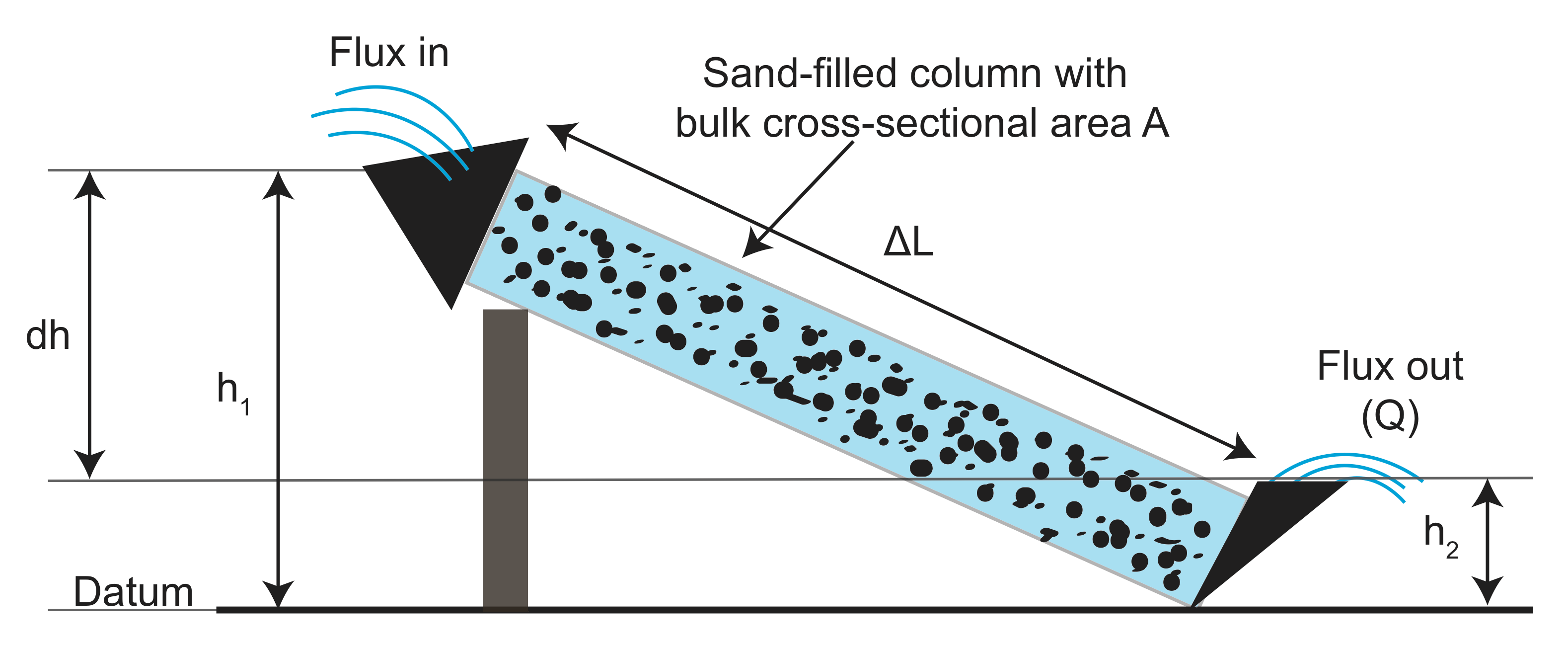
Z experimentů, shromažďují údaje o délku náhonu (\(L\)), plocha průřezu žlabu (\(A\)), výškový rozdíl (\(h_1 – h_2\)), a tok vody \(Q\) a to jak s a bez granulí (filtrování) materiál ve žlabu. Poté vykreslil měření toku normalizované plochou versus poměr výškového rozdílu k délce žlabu (\(\frac{h_1-h_2}{l}\)). To, co našel, je, že existuje lineární vztah, a sklon závisí na zrnitý materiál použil v náhonu:
\
který může být přepsán jako derivace,
\
, kde \(K\) je hydraulická vodivost a \(\frac{dh}{dx}\) je hydraulický gradient. \(Q\), celková rychlost vypouštění, má jednotky \(\frac{m^3}{s}\), objem vody za čas. Záporné znaménko je způsobeno skutečností, že tekutina proudí dolů (záporně) hydraulickým gradientem z vyšších hodnot na nižší hodnoty.
hydraulická vodivost je fyzikální parametr, který představuje, jak snadno tekutina může pohybovat prostřednictvím pórů prostor pro materiál. V Darcyho původních experimentech, použil písky s různými velikostmi zrn, nicméně, hydraulická vodivost může být určena také pro pevné horniny,protože většina hornin má určitý prostor pórů.
V návaznosti na Darcyho původní experimenty byla provedena další práce na pochopení fyzikálních vlastností tekutiny a horniny, které určují účinnou hydraulickou vodivost. Z těchto experimentů bylo zjištěno, že,
\
, kde \(k\) je vnitřní propustnosti porézní média (pevné), \(\eta\) je dynamická viskozita tekutiny, a \(\gamma = \rho g\) je měrná hmotnost kapaliny, která závisí na tom, hustota kapaliny, \(\rho\) a gravitace, \(g\).
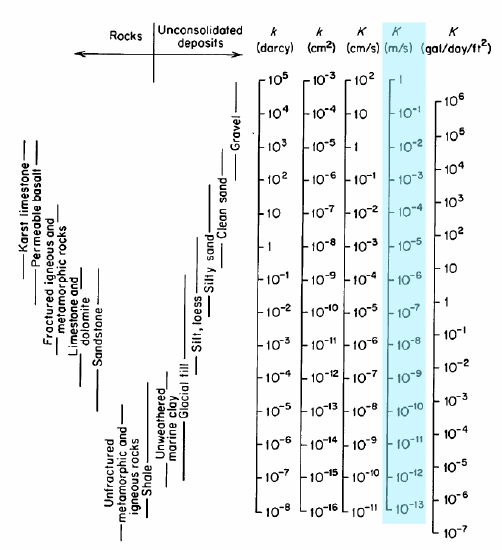
zvýrazněný sloupec v obrázku je K, hydraulická vodivost v \(\frac{m}{s}\); to jsou jednotky, které budeme používat. Hydraulická vodivost je také někdy uváděna z hlediska vnitřní propustnosti, \(k\), s jednotkami darcys nebo cm2. Celý rozsah hodnot pro hydraulickou vodivost je 1-10-13 \(\frac{m}{s}\). Experimenty jako Darcy se používají k měření K v reálných materiálech.
vypouštěcí rychlost \(Q\) je objem toku (\(m^3/s\)), ale obvykle uvažujeme proudění tekutiny z hlediska rychlosti nebo rychlosti. Absolutorium otázky mohou být přeskupeny dělením přes oblast definovat Darcy Tok
\ \
Nebo, pokud jde o vnitřní propustnost a tlakový gradient,
\
, kde \(\eta\) je viskozita tekutiny (viz níže pro odvození druhé rovnice).
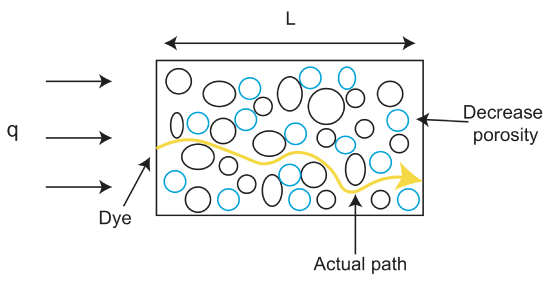
je důležité si uvědomit, že Darcyho tok se nerovná rychlosti tekutiny, i když je v jednotkách rychlosti. Rychlost tekutiny je zjištěna průměrnou lineární rychlostí (\(v_a\)), což je průměr rychlosti všech možných cest tekutiny porézním médiem: nalezení této hodnoty je však mimo rozsah této třídy. Místo toho jsme na vědomí, že rychlost proudění je
\
, kde \(\varphi\) je pórovitost a v je rychlost tekutiny. Pórovitost, \(\varphi\) se vypočítá jako poměr objemu prázdný prostor na celkový objem materiálu \(\varphi=\frac{V_{void}}{V_{tot}}\), a je obvykle vyjádřena jako zlomek mezi 0 a 1, nebo jako procenta. Všimněte si, že pokud \(\varphi\leq\) 1 pak rychlost tekutiny je větší Darcy tok.
dalším pojmem, který vzniká při diskusi o průtoku horninami a nekonsolidovanými materiály, je propustnost. Zatímco pórovitost je skutečný zlomek pórů (dutin) ve skále, tyto dutiny mohou mít různé tvary a různou konektivitu, což ovlivňuje, jak snadno se tekutina může pohybovat prostorem pórů. Propustnost je měřítkem snadnosti, s jakou mohou kapaliny a plyny procházet horninou. Čím více je materiál konsolidován, tím nižší je jeho propustnost. Tak „volné“ materiály jako štěrk mají vysokou propustnost. Některé horniny mohou mít také anizotropní propustnost, což znamená, že tekutiny mohou snadno proudit v jednom směru, ale ne v jiném. Příkladem horniny s anizotropní propustností je břidlice. Tekutiny se mohou snadno pohybovat ve vrstvě břidlice, ale nemohou se pohybovat napříč vrstvami.
rychlost kapaliny
Udělejme si základní příklad.
je nám dáno, že \(q=2 \ frac{m}{min}\) a \(\varphi\) je 25% a chceme najít rychlost tekutiny.
nejprve převedeme 25% na 0,25.
pak \(v= \ frac{2}{0.25}\frac{m}{min}\)
a
\(v=8 \ frac{m}{min}\) je rychlost tekutiny.
Hydraulické Hlavy
Návrat do Darcyho experimenty, jaký je fyzikální proces, je ve skutečnosti řídí tok tekutiny přes náhon?
výraz \(\frac{dh}{dx} \) je označován jako hydraulické čelo, což je tlak kapaliny vzhledem k hmotnosti kapaliny vzhledem k nějaké referenční místo: tlakový gradient. Nicméně \(\frac{dh}{dx} \) nemá jednotky tlaku na jednotku délky, tak proč se tomu říká hydraulická hlava?
uvažujme, jaký je tlak v oblaku v Darcyho experimentech. Aby se dělat experimenty, Darcy je měl nádrž vody na horním konci žlabu poskytuje stálou hladinu vody v horní části žlabu, což odpovídá výšce žlabu, \(h_1\). Podobně byla na dně nádrž s konstantní hladinou vody ekvivalentní \(h_2\). Proto je tlak kapaliny v každé z nádrží v důsledku hmotnosti vody dán \(P = \rho g h\). Tlakový spád mezi horní a spodní části vlečky je pak
\
nebo
\
Dosazení do Darcyho Zákon,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
Připomeňme si, že od výše hydraulická vodivost může být psán z hlediska vnitřní propustnost jako \(K = k\frac{\gamma}{\eta}\), který je ekvivalentní \(k\frac{\rho g}{\eta} \), nebo přeskupit, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Proto můžeme nahradit dát dvě rovnocenné výrazy pro Darcyho Zákon, s jedním pokudjde o přechodu na výšku,
\
a za druhé, pokud jde o přechod v tlaku,
\
Tedy \(\frac{dh}{dx}\) se nazývá hydraulický hlavu, protože fyzikální původ termínu v Darcyho Zákon je gradientu tlaku v kapalině, který řídí tok.
voda opouštějící Aquifer
pojďme nyní udělat příklad výpočtu rychlosti tekutiny vody vstupující do aquifer. Ve skici pod výškou vodonosné vrstvy následuje topografie na kopci sousedícím s údolím s potokem. Voda teče z vysokého tlaku (výška hlavy) směrem do údolí a opouští zvodnělé vrstvy u potoka. Můžeme použít Darcyho zákon k odhadu rychlosti proudění vody z vodonosné vrstvy.
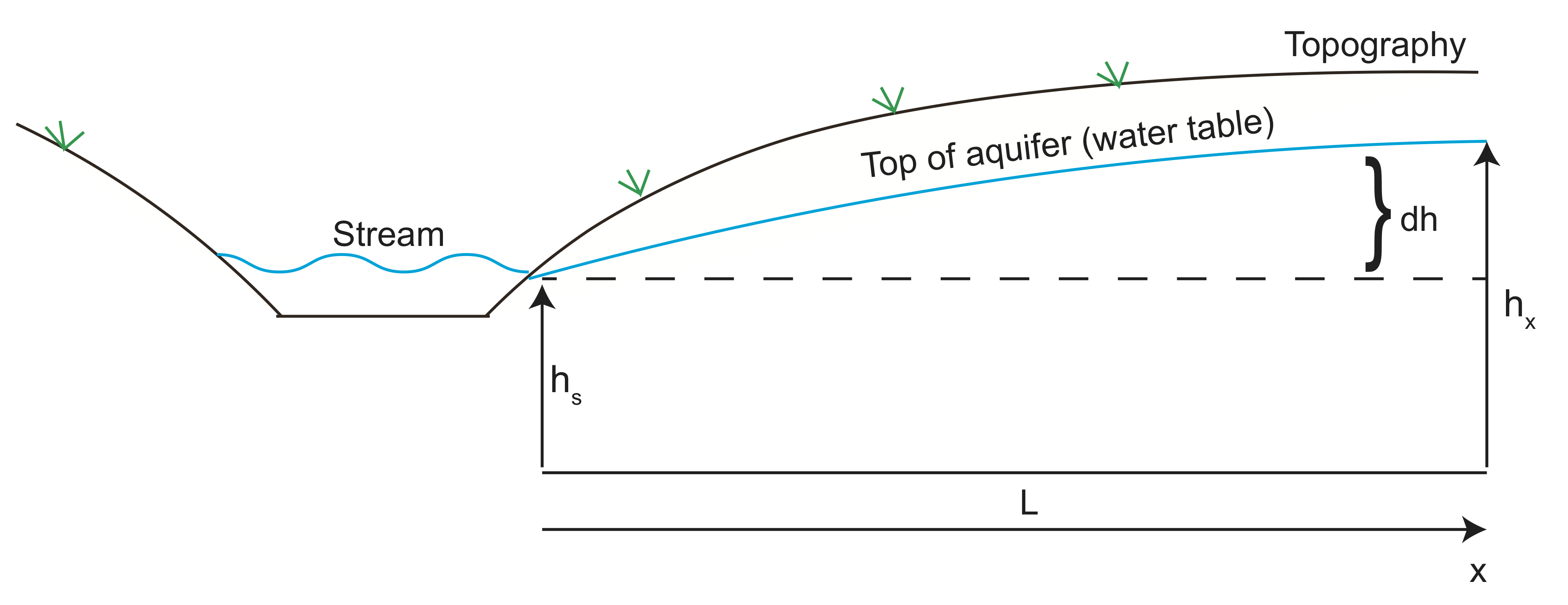
Pomocí geofyzikální imaging, výška, zvodeň je zjištěno, že být 10 m (\(dh\)) nad potokem o výšce 100 metrů (\(L\)). Předpokládejme, že hydraulická vodivost je \ (k=10^{-6}\) m / s a pórovitost je \(\varphi=30\)%.
darcy tok je
\
\
\
rychlost proudění je
\
\
\
\

Laminární vs. Turbulentní Proudění
Jedním z implicitních předpokladů, v Darcyho zákon je, že proudění je laminární. Laminární tok je charakterizován jako sestávající z tenkých vrstev nebo Lamin tekutiny, které se navzájem pohybují paralelně. Naproti tomu turbulentní tok je charakterizován víry, víry a víry, ve kterých se sousední vrstvy tekutiny rozcházejí a berou různé cesty dolů proudem.
Jeden způsob, jak můžeme vyčíslit, zda kapaliny je laminární nebo turbulentní, je výpočet Reynoldse číslo pro tok, je definována jako
\
Reynoldse číslo je zjištěno, že tím, že zvažuje dva termíny v hybnosti rovnováhy pro proudění. První člen je inerciální síla na jednotku objemu, která pohání tok, \(\rho u \ frac{du}{dx}\). Druhým termínem je viskózní síla na jednotku objemu, která odolává proudění, \(\eta\frac{d^2u}{dx^2}\). Tyto dva termíny se musí vyvážit, takže je můžeme nastavit stejně,
\
dále přepíšeme termíny zjednodušeným způsobem, abychom zachytili pouze relevantní rozměry proměnných. Dělat, musíme jít přes to, co se nazývá rozměrová analýza, ve které nahradíme každý proměnné, s referenční hodnoty, časy non-dimenzionální podobě proměnné.
například výraz \(x\) je přepsána jen jako \(L x\), kde \(L\) je referenční délka (tekutiny, hloubky) a \(x\) je non-dimenzionální vzdálenost. Podobně necháme \(u = u_o u’\). Dosazením do rovnice, dostaneme
\
dále jsme kombinovat konstantní hodnoty před
\
Všimněte si, že kombinace proměnných v přední je Tam to číslo,
\
kde jsou proměnné \(u_o\) rychlost proudění, L tekutiny hloubky, a proměnné, které jsme viděli dříve, \(\rho\) kapaliny hustota, a \(\eta\) tekutin viskozita. Procházením této analýzy zjistíme, že jakýkoli tok, který je charakterizován rovnováhou těchto dvou termínů, může být porovnán pouhým poznáním hodnoty Reynoldsova čísla. Například, pokud jeden tok má viskozitu, která je 10 krát viskozity v jiném průtoku, dva toky budou chovat stejné je hustota (nebo rychlost nebo délka) je také zvýšená o faktor 10 pro vyšší viskozity případě, že je Reynoldsovo číslo pro oba toky je stejný.
Chcete-li mít Darcyho tok, Reynoldovo číslo musí být menší než asi 1-10 (laminární). Pro \(Re>1-10 \) tok není striktně laminární, ale ještě není turbulentní (nelineární, nelaminární). Chcete-li mít turbulentní tok, Reynoldovo číslo musí být větší než asi 2000.
pochopení, že konstanty v čitateli a jmenovateli ovlivňují charakteristiky toku opačným způsobem, také pomáhají přemýšlet o tom, jak se budou různé tekutiny chovat za podobných vnějších podmínek. Například hustší tekutina, která má také rychlou rychlost, bude mít vyšší Re a bude vykazovat turbulentní chování. Naproti tomu tekutina, jako je LED, která má vysokou viskozitu a pohybuje se velmi pomalu, bude mít nízkou Re a pravděpodobně bude mít laminární tok. Vysoká viskozita ledu působí na stabilizaci toku. Jako další příklad vezměme dvě tekutiny by mohly být oba pohybují stejnou rychlostí chovat jinak, když ostatní hodnoty v Reynoldse číslo \(\frac{\rho L}{\mu}\) jsou různé. Proto se typ toku závisí nejen na rychlosti proudění, ale na kombinaci proměnných v Reynoldse číslo.
Použití Darcyho Toku
Darcyho zákon je hlavní rovnice, která upravuje proudění v zvodních a studní. Bez ní bychom nebyli schopni vrtat studny nebo pochopit pohyb vody v zvodní, a to zejména v Kalifornském central valley, kde se obě tyto myšlenky jsou důležité pro zemědělskou produktivitu a podzemních vod sedání.
