9. Impedancia y Ángulo de fase
No se pierda…
Explore la impedancia, la corriente y el voltaje en un circuito RLC en el applet más adelante en esta página.
Impedancia
La impedancia de un circuito es la resistencia efectiva total al flujo de corriente por una combinación de los elementos del circuito.Símbolo
: Unidades Z
: ‘Ω’
El voltaje total en los 3 elementos (resistencias, condensadores e inductores) se escribe
VRLC
Para encontrar este voltaje total, no podemos simplemente agregar los voltajes VR, VL y VC.
Porque VL y VC son considerados para ser imaginario cantidades, tenemos:
Impedancia VRLC = IZ
Así que la `Z = R + j(X_L− X_C)`
Ahora, la magnitud (tamaño, o valor absoluto) de Z está dada por:
`|Z|=sqrt(R^2+(X_L-X_C)^2`
ángulo de Fase
`bronceado\ theta=(X_L-X_C)/R`
Ángulo θ representa el ángulo de fase entre la corriente y el voltaje.
Compare esto con el Ángulo de fase que encontramos anteriormente en Gráficos de y = a sin(bx + c).
Ejemplo 1
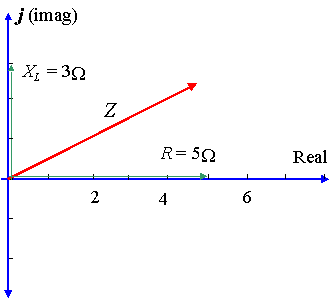
Un circuito tiene una resistencia de` 5\ Ω ‘ en serie con una reactancia a través de un inductor de `3\ Ω`. Representan la impedancia por un número complejo en forma polar.
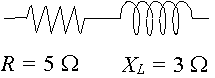
Respuesta
En este caso, `X_L= 3\ Ω` y `X_C= 0` así que `X_L – X_C= 3\ Ω`.
Entonces, en forma rectangular, la impedancia se escribe:
`Z = 5 + 3j\ Ω`
Usando calculadora, la magnitud de Z viene dada por: `5.83`, y el ángulo `θ` (la diferencia de fase) viene dada por: `30.96^@`.
Por lo que el voltaje conduce a la corriente en ‘ 30.96^@’, como se muestra en el diagrama.
Presentando Z como un número complejo (en forma polar), tenemos:
`Z = 5.83 3 30.96^@\ Ω`.
Ejemplo 2 (a)
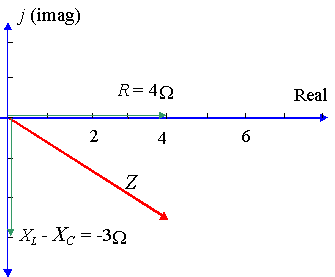
Un circuito de ca en particular tiene una resistencia de `4\ Ω`, una reactancia a través de un inductor de `8\ Ω` y una reactancia a través de un condensador de `11\ Ω`. Expresa la impedancia del circuito como un número complejo en forma polar.
Respuesta
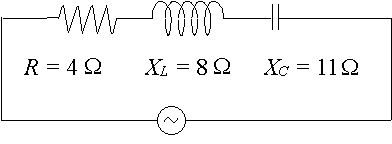
En este caso, tenemos: `X_L – X_C= 8 – 11 = -3\ Ω`
So `Z = 4 – 3j\ Ω` en forma rectangular.
Ahora para expresarlo en forma polar:
Usando calculadora, encontramos `r = 5 ` y`θ = -36.87^@’.
So `Z = 5 Z -36.87^@\ Ω`
Gráfico RLC interactivo
A continuación se muestra un gráfico interactivo con el que jugar (no es una imagen estática). Puede explorar el efecto de una resistencia, un condensador y un inductor sobre la impedancia total en un circuito de CA.
Actividades para este Interactivo
- Primero, simplemente juega con los controles deslizantes. Puede:
Arrastrar el control deslizante superior a la izquierda o a la derecha para variar la impedancia debido a la resistencia, `R`,
Arrastrar el control deslizante XL hacia arriba o hacia abajo para variar la impedancia debido al inductor, `X_L`, y
Arrastrar el control deslizante XC hacia arriba o hacia abajo para variar la impedancia debido al condensador, `X_C`. - Observe los efectos de diferentes impedancias en los valores de XL-XC y Z.
- Observe los efectos de diferentes impedancias en θ, el ángulo que la línea roja de «resultado» hace con la horizontal (en radianes).
- Considere los gráficos de voltaje y corriente en el interactivo. Observe la cantidad de retraso o ventaja a medida que cambia los controles deslizantes.
- ¿Qué has aprendido jugando con este interactivo?