2.5: Flujo de la Ley de Darcy en un Medio Poroso
La ley de Darcy es crucial para comprender muchas ramas de la geología, especialmente la hidrogeología. Antes de ver la ley y lo que puede decirnos, veamos cómo se desarrolló. La ley de Darcy lleva el nombre de Henry Darcy, un ingeniero francés del siglo XIX que desarrolló un sistema de tuberías subterráneas a presión para entregar agua alrededor de la ciudad de Dijon. El sistema, que también proporcionaba agua a las famosas fuentes de Dijon, revolucionó los sistemas de agua y alcantarillado de la ciudad. El sistema no requería bombas y era impulsado exclusivamente por gravedad. Durante el proceso de desarrollo del nuevo sistema, Darcy llevó a cabo una serie de experimentos en los que trató de mover el agua utilizando únicamente la gravedad.
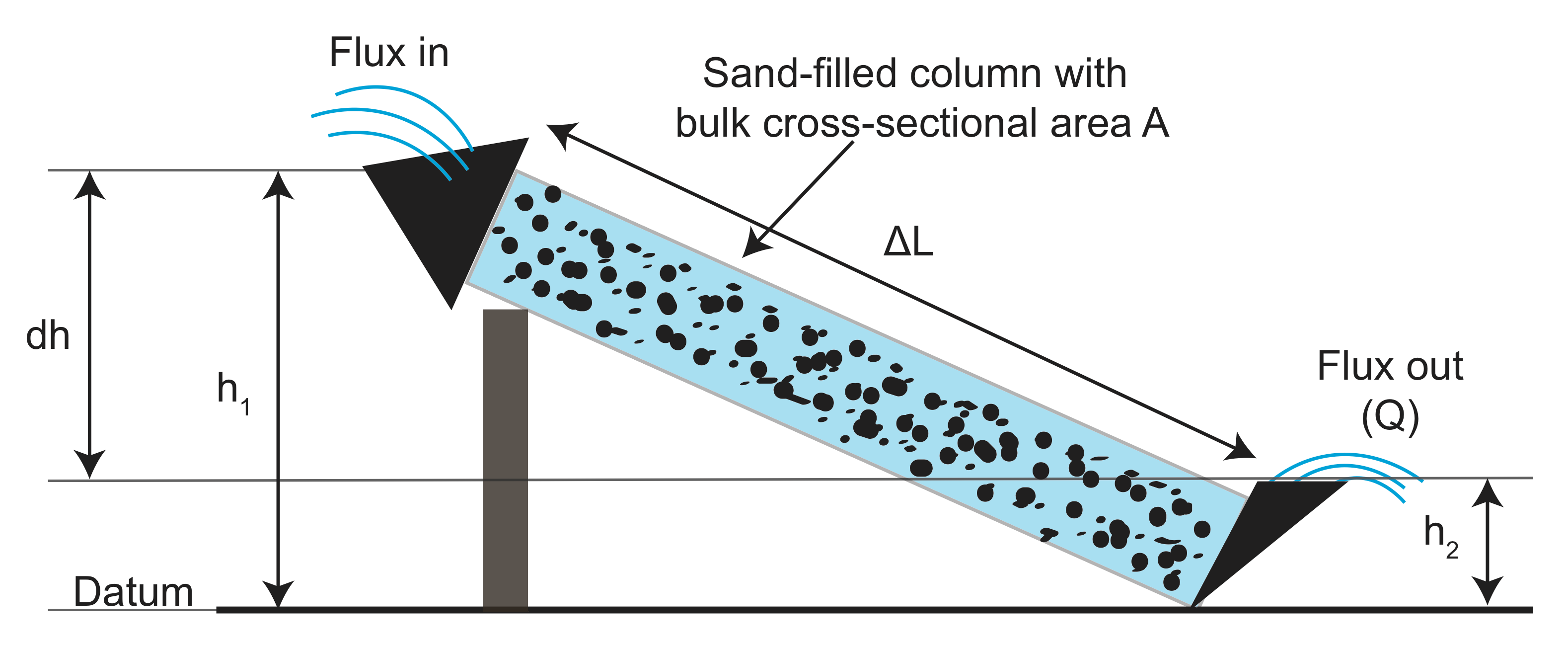
De los experimentos, los datos recopilados sobre la longitud del canal (\(L\)), el área de la sección transversal del canal (\(A\)), la diferencia de altura (\(h_1 – h_2\)) y el flujo de agua que sale \(Q\) tanto con como sin material granular (filtrado) en el canal. A continuación, trazó la medición de flujo normalizada por el área versus la relación entre la diferencia de altura y la longitud del canal (\( \frac{h_1 – h_2}{l}\)). Lo que encontró es que existe una relación lineal y la pendiente depende del material granulado que se utiliza en el canal:
\
que puede ser reescrito como un derivado,
\
donde \(K\) es la conductividad hidráulica y \(\frac{dh}{dx}\) es el gradiente hidráulico. \(Q\), la tasa de descarga total, tiene unidades de \(\frac{m^3}{s}\), el volumen de agua por tiempo. El signo negativo se debe al hecho de que el fluido fluye hacia abajo (negativo) el gradiente hidráulico de valores más altos a valores más bajos.
La conductividad hidráulica es un parámetro físico que explica la facilidad con que el fluido puede moverse a través del espacio de poros del material. En los experimentos originales de Darcy, utilizó arenas con diferentes tamaños de grano, sin embargo, la conductividad hidráulica también se puede determinar para rocas sólidas, ya que la mayoría de las rocas tienen algo de espacio en los poros.
Siguiendo los experimentos originales de Darcy, se realizó un trabajo adicional para comprender las propiedades físicas del fluido y la roca que determinan la conductividad hidráulica efectiva. A partir de estos experimentos se encontró que,
\
donde \(k\) es la permeabilidad intrínseca de los medios porosos (sólido), \(\eta\) es la viscosidad dinámica del fluido, y \(\gamma = \rho g\) es el peso específico del fluido, la cual depende de la densidad del fluido, \(\rho\) y la gravedad, \(g\).
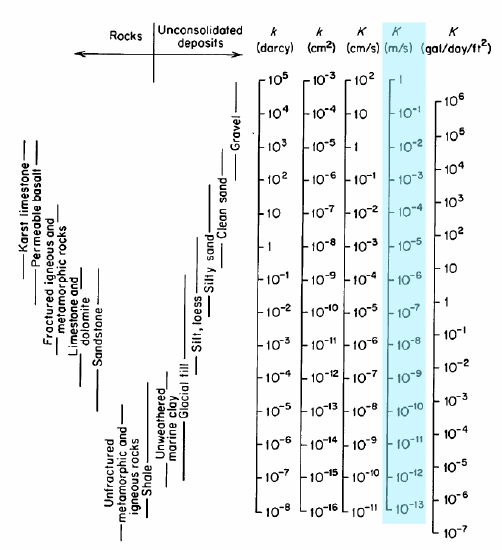
La columna resaltada en la figura es K, la conductividad hidráulica en \(\frac{m}{s}\); estas son las unidades que utilizaremos. La conductividad hidráulica también se reporta a veces en términos de permeabilidad intrínseca, \(k\), con unidades de darcys o cm2. El rango completo de valores de conductividad hidráulica es de 1-10-13 \(\frac{m}{s}\). Experimentos como el de Darcy se utilizan para medir K en materiales reales.
La velocidad de descarga \(Q\) es un flujo de volumen (\(m^3/s\)), pero generalmente pensamos en el flujo de fluido en términos de una velocidad o velocidad. Las preguntas de descarga se pueden reorganizar dividiendo por el área para definir el flujo de Darcy
\\]
O en términos de la permeabilidad intrínseca y el gradiente de presión,
\
donde \(\eta\) es la viscosidad del fluido (vea a continuación la derivación de la segunda ecuación).
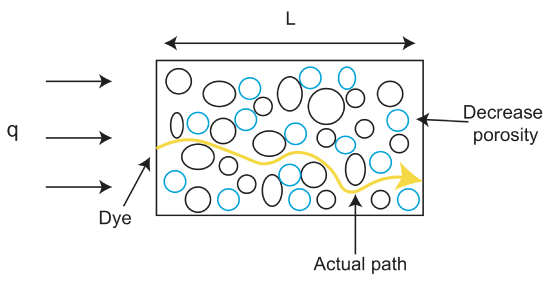
Es importante tener en cuenta que el flujo Darcy no es igual a la velocidad del fluido, a pesar de que está en unidades de velocidad. La velocidad del fluido se encuentra a través de la velocidad lineal promedio (\(v_a\)), que es el promedio de la velocidad de todos los caminos posibles del fluido a través del medio poroso: pero encontrar este valor está fuera del alcance de esta clase. En su lugar, notaremos que la velocidad del fluido es
\
donde \(\varphi\) es la porosidad y v es la velocidad del fluido. La porosidad, \(\varphi\) se calcula como la relación entre el volumen del espacio vacío y el volumen total de un material \(\varphi=\frac{V_{vacío}}{V_{tot}}\), y generalmente se expresa como una fracción entre 0 y 1 o como un porcentaje. Tenga en cuenta que si \(\varphi\leq\)1, entonces la velocidad del fluido es mayor que el flujo de darcy.
Otro término que surge cuando se habla del flujo a través de rocas y materiales no consolidados es la permeabilidad. Si bien la porosidad es la fracción real de poros (vacíos) en la roca, estos vacíos pueden tener diferentes formas y conectividad, lo que afecta la facilidad con que un fluido puede moverse a través del espacio de poros. La permeabilidad es una medida de la facilidad con la que los líquidos y gases pueden pasar a través de una roca. Cuanto más consolidado sea el material, menor será su permeabilidad. Por lo tanto, los materiales» sueltos » como la grava tienen una alta permeabilidad. Algunas rocas también pueden tener permeabilidad anisotrópica, lo que significa que los fluidos pueden fluir fácilmente en una dirección, pero no en otra. Un ejemplo de una roca con permeabilidad anisotrópica es un esquisto. Los fluidos pueden moverse fácilmente dentro de una capa de esquisto, pero no pueden moverse a través de capas.
Velocidad del fluido
Hagamos un ejemplo básico.
Se nos da que \(q=2\frac{m}{min}\) y \(\varphi\) es 25% y queremos encontrar la velocidad del fluido.
Primero convertimos el 25% a 0.25.
Entonces, \(v = \frac{2} {0.25}\frac{m}{min}\)
y
\(v=8 \frac{m}{min}\) es la velocidad del fluido.
Cabezal hidráulico
Volviendo a los experimentos de Darcy, ¿qué es el proceso físico que en realidad impulsa el flujo de fluido a través del canal?
El término \(\frac{dh} {dx}\) se conoce como el cabezal hidráulico, que es la presión del líquido debida al peso de un fluido en relación con algún lugar de referencia: un gradiente de presión. Sin embargo, \(\frac{dh} {dx}\) no tiene unidades de presión por unidad de longitud, así que ¿por qué se llama cabezal hidráulico?
Consideremos cuál es la presión en el canal en los experimentos de Darcy. Para hacer los experimentos, Darcy’s tenía un tanque de agua en el extremo superior del canal que proporcionaba un nivel constante de agua en la parte superior del canal, equivalente a la altura del canal, \(h_1\). De manera similar, había un tanque en la parte inferior con un nivel constante de agua equivalente a \(h_2\). Por lo tanto, la presión del fluido en cada uno de los tanques debido al peso del agua viene dada por \(P = \rho g h\). El gradiente de presión entre la parte superior e inferior de la pluma es entonces
\
o
\
Sustituyendo en la Ley de Darcy,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
el Recuerdo, de lo anterior que la conductividad hidráulica puede ser escrito en términos de la permeabilidad intrínseca como \(K = k\frac{\gamma}{\eta}\), que es equivalente a \(k\frac{\rho g}{\eta} \) o reorganización, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Por lo tanto, podemos sustituir para dar dos expresiones equivalentes para la Ley de Darcy, con una interms del gradiente en altura,
\
y la segunda en términos del gradiente en presión,
\
Así, \(\frac{dh}{dx}\) se llama la cabeza hidráulica porque el origen físico del término en la Ley de Darcy es el gradiente de presión en el fluido, que impulsa el flujo.
Agua que sale de un acuífero
Hagamos ahora un ejemplo calculando la velocidad del fluido del agua que entra en un acuífero. En el dibujo debajo de la altura del acuífero sigue la topografía de la colina adyacente al valle con el arroyo. El agua fluye desde alta presión (altura de la cabeza) hacia el valle y deja el acuífero en el arroyo. Podemos usar la Ley de Darcy para estimar la velocidad del flujo de agua del acuífero.
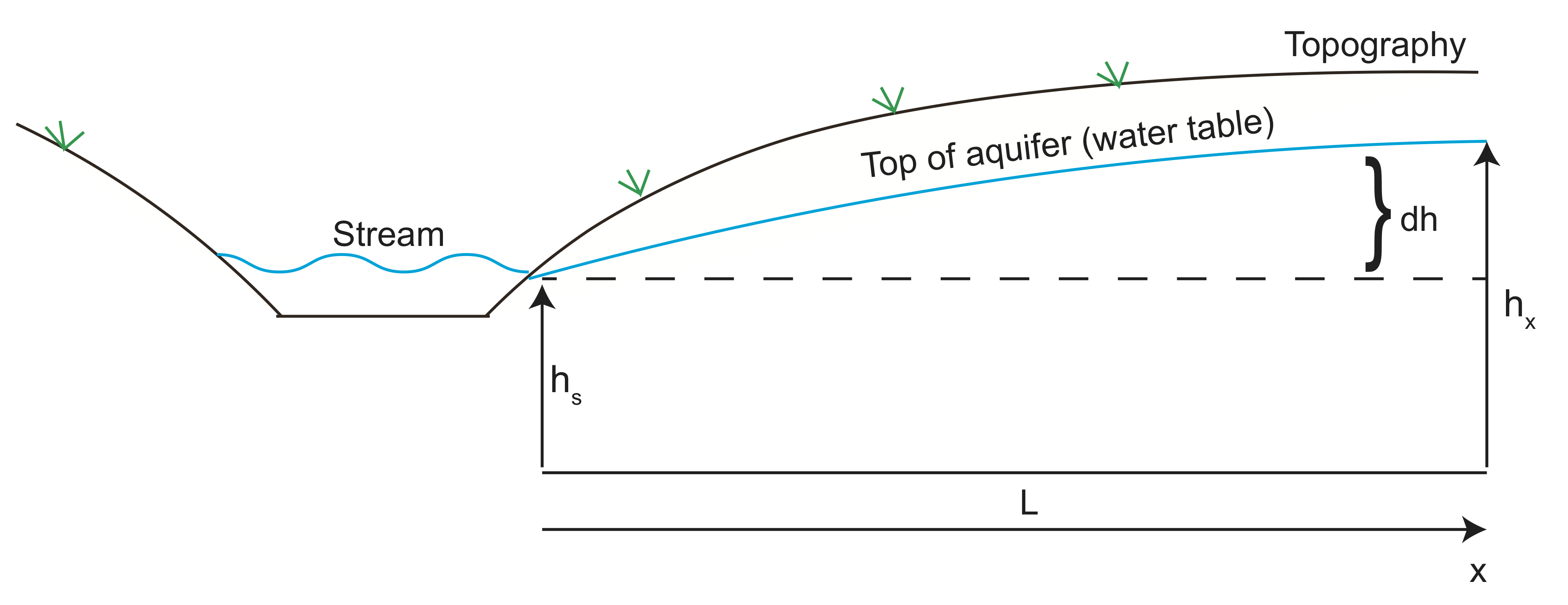
Utilizando imágenes geofísicas, la altura del acuífero se encuentra a 10 m (\(dh\)) por encima de la altura de la corriente a unos 100 metros (\(L\)) de distancia. Supongamos que la conductividad hidráulica es \ (K = 10^{-6}\) m/s y la porosidad es \(\varphi=30\)%.
El darcy de flujo
\
\
\
La velocidad del fluido es
\
\
\
\

Flujo Laminar versus Flujo Turbulento
Una de las suposiciones implícitas en la ley de Darcy es que el flujo es laminar. El flujo laminar se caracteriza por consistir en capas delgadas o láminas de fluido que se mueven paralelas entre sí. En contraste, el flujo turbulento se caracteriza por remolinos, vórtices y remolinos, en los que las capas adyacentes de fluido divergen y toman diferentes caminos hacia abajo.
Una forma de cuantificar si un fluido es laminar o turbulento es calculando el número de Reynold para el flujo, definido como
\
El número de Reynold se encuentra considerando los dos términos en el balance de momento para el flujo. El primer término es la fuerza inercial por unidad de volumen, que impulsa el flujo, \(\rho u\frac {du} {dx}\). El segundo término es la fuerza viscosa por unidad de volumen, que resiste el flujo, \(\eta \ frac{d^2u}{dx^2}\). Estos dos términos deben equilibrarse, para que podamos establecerlos iguales,
\
A continuación, reescribimos los términos, de una manera simplificada para capturar solo las dimensiones relevantes de las variables. Para hacer, pasamos por lo que se llama un análisis dimensional, en el que reemplazamos cada variable, con valores de referencia, por una forma no dimensional de la variable.
Por ejemplo, para el término \(x\) se reescribe como \(L x’\), donde \(L\) es la longitud de referencia (la profundidad del fluido) y \(x’\) es la distancia no dimensional. Del mismo modo, dejamos \(u = u_o u’\). Sustituyéndolos en la ecuación, obtenemos
\
A continuación combinamos los valores constantes en el frente
\
Tenga en cuenta que la combinación de variables en el frente es el número de Reynold
\
donde las variables son \(u_o\) velocidad de flujo, L profundidad del fluido y las variables que hemos visto anteriormente, \(\rho\) densidad del fluido y \(\eta\) viscosidad del fluido. Al pasar por este análisis, encontramos que cualquier flujo que se caracteriza por el equilibrio de estos dos términos puede compararse simplemente conociendo el valor del número de Reynolds. Por ejemplo, si un flujo tiene una viscosidad que es 10 veces la viscosidad en otro flujo, los dos flujos se comportarán igual si la densidad (o velocidad o longitud) también se incrementa en un factor de 10 para el caso de mayor viscosidad; es decir, el número de Reynolds para los dos flujos es el mismo.
Para tener flujo Darcy, el número de Reynold debe ser menor que aproximadamente 1-10 (laminar). Para \(Re>1-10 \) el flujo no es estrictamente laminar, pero todavía no es turbulento (no-lineal, no-laminar). Para tener flujo turbulento, el número de Reynold debe ser mayor que aproximadamente 2000.
Entender que las constantes en el numerador y denominador afectan las características del flujo de la manera opuesta, también ayuda a pensar en cómo se comportarán los diferentes fluidos en condiciones externas similares. Por ejemplo, un fluido más denso que también tiene una velocidad rápida tendrá un comportamiento turbulento y Re más alto. En contraste, un fluido como el hielo que tiene una alta viscosidad y se mueve muy lentamente tendrá un bajo Re y probablemente tendrá flujo laminar. La alta viscosidad del hielo actúa para estabilizar el flujo. Como otro ejemplo, considere que dos fluidos podrían moverse a la misma velocidad y comportarse de manera diferente si los otros valores en el número de Reynold \(\frac{\rho L}{\mu}\) son diferentes. Por lo tanto, el tipo de flujo depende no solo de la velocidad de flujo, sino de la combinación de variables en el número de Reynold.
Aplicación del flujo de Darcy
La ley de Darcy es la ecuación principal que rige el flujo en acuíferos y pozos. Sin ella, no podríamos perforar pozos ni entender el movimiento del agua en los acuíferos, especialmente en el valle central de California, donde ambas ideas son cruciales para la productividad agrícola y el hundimiento de las aguas subterráneas.
